Wechselspannung an Spule

19.5 Wechselspannung an Spule

Schaltung:

Anstelle einer Gleichspannung soll nun eine Wechselspannung

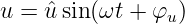u = ˆusin(ωt + φu )

(19.5.1)

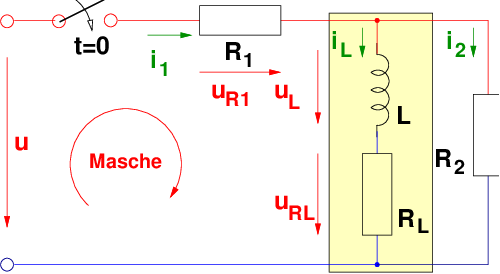
an eine Spule entsprechend Abb. 19.5.1 geschaltet werden.

Abbildung 19.5.1: Geschaltete Wechselspannung an ein Netzwerk mit Spule

Gesucht:

Strom i_L(t) durch die Spule.

FRAGE:

Was könnte sich im Vergleich zum Gleichstromfall ändern?

ANTWORTEN:

1. DGL:

In der Maschengleichung

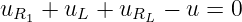uR1 + uL + uRL − u = 0

(19.5.2)

werden zuerst die Bauelementgleichungen eingesetzt

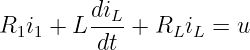diL R1i1 + L ----+ RLiL = u dt

(19.5.3)

Aus der Knotengleichung

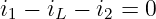i1 − iL − i2 = 0

(19.5.4)

wird der Strom i₁

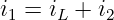i1 = iL + i2

(19.5.5)

ersetzt und dabei der Strom i₂ in der Parallelschaltung mit dem ohmschen Gesetz bestimmt

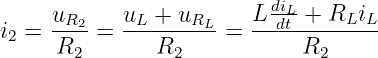uR2- uL-+-uRL- L-diLdt-+-RLiL-- i2 = R = R = R 2 2 2

(19.5.6)

Zusammen mit der Wechselspannung ergibt sich

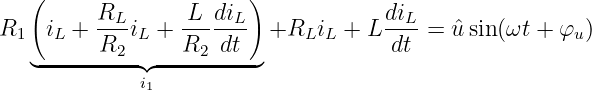( R L di ) di R1 iL + --LiL + -----L- +RLiL + L --L-= ˆu sin (ωt + φu) ◟-----R2--◝◜--R2--dt-◞ dt i1

(19.5.7)

und zusammengefasst

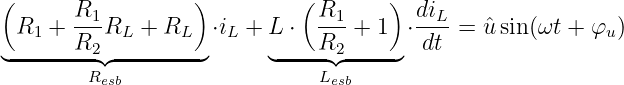( ) ( ) R1- R1- diL- R1 + R2 RL + RL ⋅iL + L ⋅ R2 + 1 ⋅dt = ˆusin(ωt + φu ) ◟--------◝◜--------◞ ◟-----◝◜----◞ Resb Lesb

(19.5.8)

ESB:

Mit dem Ersatzwiderstand R_esb und der Ersatzinduktivität L_esb vereinfacht sich die DGL zu⁴

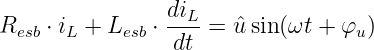diL- Resb ⋅ iL + Lesb ⋅ dt = ˆusin(ωt + φu )

(19.5.9)

FRAGE:

Wie sieht die DGL aus, wenn nur eine Spule ohne die Widerstände R₁ und R₂ an die Wechselspannung geschaltet wird?

ANTWORT:

2. Netzwerkber.:

Die Berechnung des eingeschwungenen Zustandes erfolgt mit der Symbolischen Methode im Bildbereich (Komplexe Rechnung). Mit der Stromteilerregel

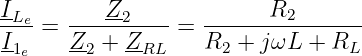ILe-= ---Z2-----= ------R2-------- I1e Z2 + ZRL R2 + jωL + RL

(19.5.10)

und dem eingeschwungenen Gesamtstrom

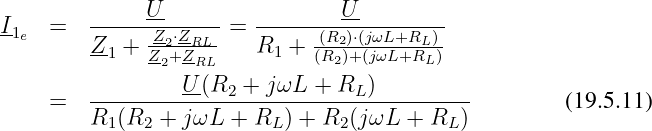
U- U- I1e = ------Z2⋅ZRL- = ------(R2)⋅(jωL+RL-)- Z1 + Z2+ZRL R1 + (R2)+(jωL+RL ) U-(R + jωL + R ) = --------------2-----------L---------- (19.5.11) R1 (R2 + jωL + RL ) + R2(jωL + RL )

ergibt sich der eingeschwungene Strom zu

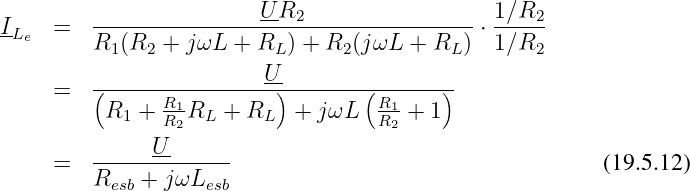
U-R2 1 ∕R2 ILe = -------------------------------------⋅----- R1 (R2 + jωL + RL ) + R2 (jωL + RL ) 1 ∕R2 (---------------U-)-------(------)- = R + R1R + R + jωL R1-+ 1 1 R2 L L R2 ------U------- = Resb + jωLesb (19.5.12)

Weg:

Was haben wir gerade gerechnet?

Wir haben in der Originalschaltung etwas aufwendig gerechnet und dann am Ende in das Ergebns den Ersatzwiderstand R_esb und die Ersatzinduktivität L_esb eingesetzt.

Einfacher:

Wenn wir den Sinn der Ersatzschaltung verstanden haben, können wir aber auch gleich in der Ersatzsschaltung

eine Maschengleichung einfacher direkt mit mit den Ersatzkomponenten aufstellen

und erhalten damit etwas einfacher direkt den eingeschwungene Strom zu

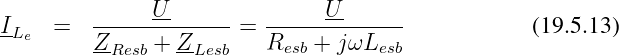
U- U- ILe = --------------= -------------- (19.5.13) ZResb + ZLesb Resb + jωLesb

Zurück:

Die Rücktransformation der komplexen Zeitfunktion

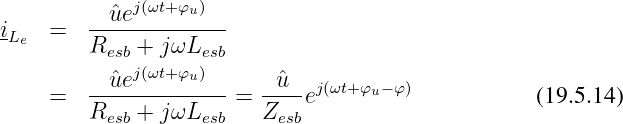
ˆuej(ωt+ φu) iLe = R----+-jωL---- esb esb --ˆuej(ωt+-φu)-- -ˆu-- j(ωt+φu−φ) = Resb + jωLesb = Zesbe (19.5.14)

mit der Amplitude

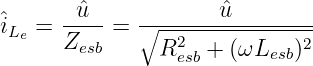
ˆiLe = --ˆu- = ∘------ˆu--------- Zesb R2esb + (ωLesb)2

und dem Anfangsphasenwinkel

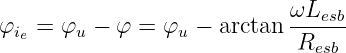
ωLesb- φie = φu − φ = φu − arctan Resb

liefert den eingeschwungenen Strom

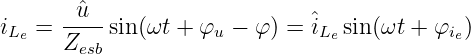-ˆu-- iLe = Z sin(ωt + φu − φ ) = ˆiLe sin(ωt + φie) esb

(19.5.15)

3. Hom. DGL:

Die Lösung der homogenen DGL⁵

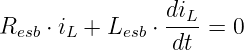Resb ⋅ iL + Lesb ⋅ diL-= 0 dt

(19.5.16)

wird mit dem Exponentialansatz zu

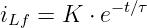
iLf = K ⋅ e−t∕τ

Eingesetzt in die DGL

[ ] K ⋅ e−t∕τ Resb − Lesb = 0 τ

ergibt sich die Zeitkonstante

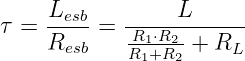Lesb L τ = R--- = R1⋅R2------- esb R1+R2 + RL

(19.5.17)

→ u = 0 in der homogenen DGL führt dazu, dass die Widerstände R₁ und R₂ parallel liegen und in Reihe zu R_L den Gesamtwiderstand der Zeitkonstanten bestimmen.

AUFGABE:

Führen Sie ausgehend von den Gleichungen für L_esb und R_esb die Umformung der Gleichung für τ durch⁶!

ERGEBNIS:

4. Konstanten:

Für die Anfangsbedingung

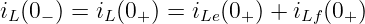iL(0− ) = iL(0+) = iLe(0+) + iLf(0+)

(19.5.18)

erhalten wir aus Gln. 19.5.15 mit

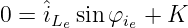
0 = ˆiLe sin φie + K

die Konstante zu

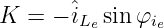ˆ K = − iLe sinφie

(19.5.19)

und damit die Lösung der homogenen DGL zu

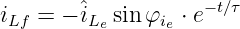− t∕τ iLf = −ˆiLe sin φie ⋅ e

(19.5.20)

5. Überlagerung:

Die Überlagerung der beiden Lösungen ergibt den Ausgleichsvorgang

[ ] iL = iLe + iLf = ˆiLe sin(ωt + φie) − sinφie ⋅ e−t∕τ

(19.5.21)

6. Berechnung:

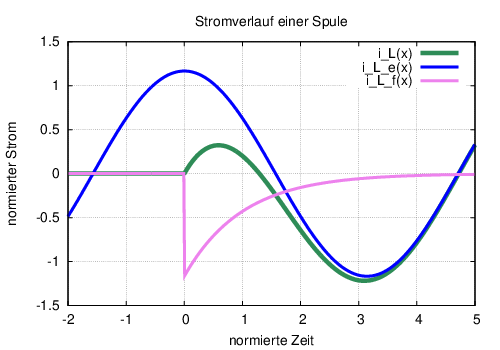
Die normierte Darstellung des Stromverlaufs beim Einschalten einer Wechselspannung an eine Spule in Abb. 19.5.2 zeigt die Addition des flüchtigen Stroms, der den eingeschwungenen Strom für t = t₀ zu Null kompensiert.

Abbildung 19.5.2: Stromverlauf beim Einschalten einer Wechselspannung an eine Spule

FRAGE:

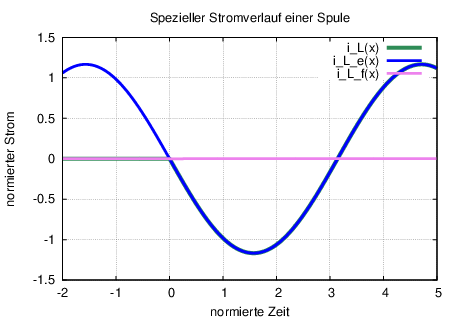
Wann muss geschaltet werden, damit der Ausgleichsstrom sofort gleich dem eingeschwungenen Strom wird?

ANTWORT:

Abbildung 19.5.3: Minimaler Stromverlauf beim Einschalten einer Wechselspannung an eine Spule

FRAGE:

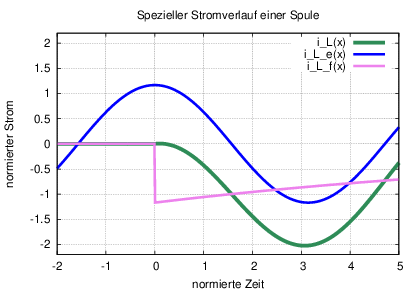
Wie groß kann der Ausgleichsstrom maximal unter welchen Bedingungen werden?

ANTWORT:

Abbildung 19.5.4: Maximaler Stromverlauf beim Einschalten einer Wechselspannung an eine Spule

⁴Sie entspricht damit der Gln. 19.3.2

⁵Auch bei einer Wechselspannung ist die Störfunktion Null bei der homogenen DGL.

⁶Das Ergebnis ist der Weg des Stromes bei kurzgeschlossener Spannungsquelle!

[next] [prev] [prev-tail] [front] [up]