Wechselspannung an Reihenschwingkreis

19.6 Wechselspannung an Reihenschwingkreis

RLC:

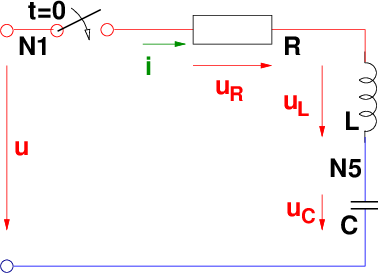
Als letztes soll nun eine Wechselspannung an einen RLC-Reihenschwingkreis entsprechend Abb. 19.6.1 geschaltet werden. Gesucht ist der Strom i(t) nach dem Schalten⁷.

Abbildung 19.6.1: Geschaltete Wechselspannung an einen RLC-Schwingkreis und LTspice-Simulation

→ Würde hier anstelle der Wechselspannung eine Gleichspannung geschaltet, so wäre aufgrund des Kondensators der eingeschwungene Zustand gleich dem Ausgleichsvorgang.

1. DGL:

Aus der Maschengleichung

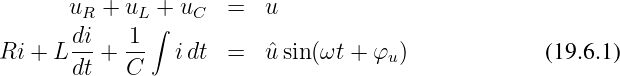
uR + uL∫+ uC = u Ri + L di+ 1- idt = ˆu sin (ωt + φ ) (19.6.1) dt C u

ergibt sich mit einmaliger Differentiation die DGL⁸

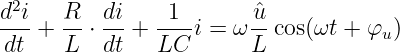2 d-i R- di -1-- uˆ dt + L ⋅dt + LC i = ωL cos(ωt + φu )

(19.6.2)

2. Netzwerkber.:

Die Berechnung der partikulären Lösung des eingeschwungenen Strom ergibt im Bildbereich

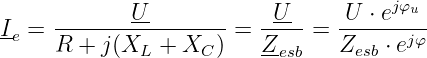U- U- U ⋅ ejφu Ie = -----------------= ---- = -------jφ R + j(XL + XC ) Zesb Zesb ⋅ e

(19.6.3)

Die Rücktransformation der komplexen Zeitfunktion liefert den eingeschwungenen Strom

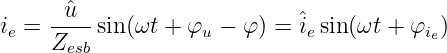i = -ˆu--sin(ωt + φ − φ ) = ˆi sin(ωt + φ ) e Zesb u e ie

(19.6.4)

3. Hom. DGL:

In die homogene DGL

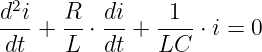d2i R- di -1-- dt + L ⋅ dt + LC ⋅ i = 0

(19.6.5)

wird der allgemeine Exponentialansatz

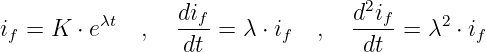
2 if = K ⋅ eλt , dif = λ ⋅ if , d-if = λ2 ⋅ if dt dt

eingesetzt

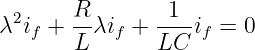
λ2if + R-λif + -1--if = 0 L LC

und ergibt so die charakteristische Gleichung

( R 1 ) if λ2 + --λ + ---- = 0 ◟-----L-◝◜---LC--◞ charakteristische Gleichung

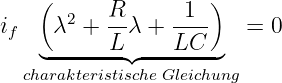
Die Lösung dieser quadratischen Gleichung ist⁹

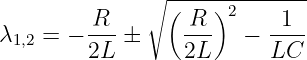∘ (---)2-------- λ = − -R- ± -R- − -1-- 1,2 2L 2L LC

(19.6.6)

Kenngrößen:

Eine alternative Darstellung der Nullstellen λ_1,2 des charakteritischen Polynoms ergibt sich mit den Kenngrößen der Schwingkreise. Mit dem Kennwiderstand

∘--- L- XK = C

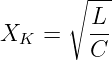
und der Güte

Q = XK-- R

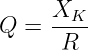
bzw. der Dämpfung

1 d = -- Q

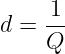
wird der Dämpfungsgrad zu

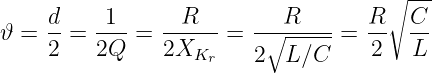∘ --- d 1 R R R C ϑ = --= --- = ------= -∘------= -- -- 2 2Q 2XKr 2 L ∕C 2 L

(19.6.7)

Mit der Resonanzfrequenz

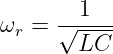
1 ωr = √----- LC

wird das Produkt zu

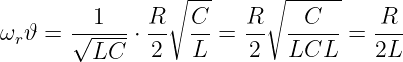∘ --- ∘ ------ 1 R C R C R ωrϑ = √-----⋅-- -- = -- -----= --- LC 2 L 2 LCL 2L

(19.6.8)

Eingesetzt in die Ergebnisgleichung erhalten wir damit

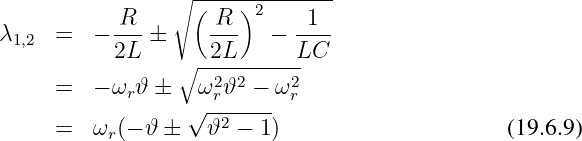
∘ -------------- R ( R )2 1 λ1,2 = − 2L- ± 2L- − LC-- ∘---------- = − ωrϑ ± ω2rϑ2 − ω2r √ --2---- = ωr (− ϑ ± ϑ − 1 ) (19.6.9)

4. Konstanten:

Es gibt drei unterschiedliche Fälle

Fall 1:

Im Aperiodischen Fall für ϑ > 1 gibt es zwei unterschiedliche negativ reelle Lösungen

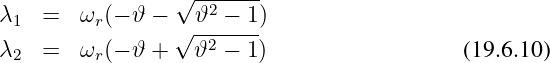
√ ------- λ1 = ωr (− ϑ − √ ϑ2-−-1) λ2 = ωr (− ϑ + ϑ2 − 1) (19.6.10)

Eingesetzt in die Lösung der homogenen DGL wird

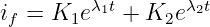λ t λ t if = K1e 1 + K2e 2

(19.6.11)

Da sich der Spulenstrom nicht sprunghaft ändert, ergibt sich aus der Anfangsbedingung

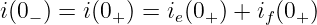i(0− ) = i(0+) = ie(0+) + if(0+ )

(19.6.12)

die erste Gleichung zur Bestimmung der Konstanten

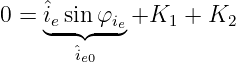0 = ˆiesinφie +K1 + K2 ◟--◝◜--◞ ˆie0

(19.6.13)

oder

K1 = −ˆie0 − K2 ˆ K2 = −ie0 − K1 (19.6.14)

Da sich die Kondensatorspannung nur stetig von u_C₀ = 0 ändern kann und die Spannung am Widerstand (i_f₀ = i_L₀ = 0) für t = 0 ebenfalls Null ist muss die Spulenspannung gleich der eingeprägten Spannung zum Schaltzeitpunkt sein

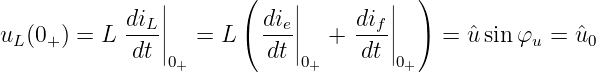| ( | | ) diL|| die|| dif|| uL(0+ ) = L dt-|| = L ( dt-|| + dt-|| ) = uˆsinφu = ˆu0 0+ 0+ 0+

(19.6.15)

mit der Ableitung des eingeschwungenen Stromanteils

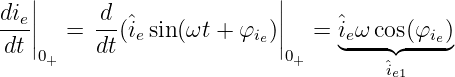|| || die|| = -d(ˆi sin(ωt + φ )|| = ˆi ω cos(φ ) dt |0 dt e ie |0 ◟e---◝◜--ie◞ + + ˆie1

(19.6.16)

und der Ableitung des flüchtigen Stromanteils

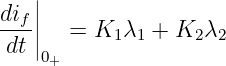|| dif|| = K1 λ1 + K2λ2 dt |0+

(19.6.17)

ergibt sich die zweite Bestimmungsgleichung zu

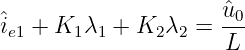ˆ ˆu0- ie1 + K1 λ1 + K2λ2 = L

(19.6.18)

Durch einsetzen von K₂ = −(î_e0 + K₁) erhalten wir

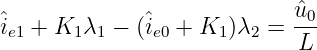ˆu ˆie1 + K1 λ1 − (ˆie0 + K1 )λ2 =--0 L

(19.6.19)

und weiter

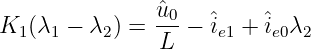K (λ − λ ) = uˆ0-− ˆi + ˆi λ 1 1 2 L e1 e0 2

(19.6.20)

Für die zweite Konstante gehen wir entsprechend vor und erhalten damit beide Konstanten zu

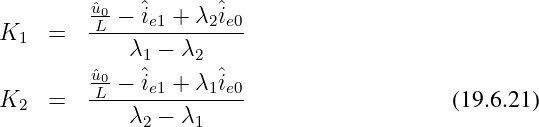
uˆ0 ˆ ˆ K = -L-−-ie1 +-λ2-ie0 1 λ1 − λ2 uˆ0 − ˆi + λ ˆi K2 = -L----e1----1e0 (19.6.21) λ2 − λ1

Fall 2:

Im Aperiodischen Grenzfall für ϑ = 1 gibt es nur eine Lösung

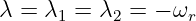λ = λ1 = λ2 = − ωr

(19.6.22)

Eingesetzt in die Lösung der homogenen DGL wird

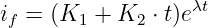λt if = (K1 + K2 ⋅ t)e

(19.6.23)

Aus dem stetigen Spulenstrom (Gln. 19.6.12) ergibt sich die erste Gleichung zur Bestimmung der Konstanten

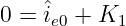0 = ˆie0 + K1

(19.6.24)

Für die stetige Kondensatorspannung (Gln. 19.6.15) benötigen wir wieder die Ableitung des flüchtigen Stromanteils¹⁰

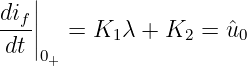di || --f|| = K1 λ + K2 = ˆu0 dt |0+

(19.6.25)

Die beiden Konstanten werden damit

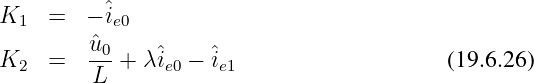
ˆ K1 = − ie0 K = ˆu0-+ λˆi − ˆi (19.6.26) 2 L e0 e1

Fall 3:

Im Periodischen Fall für ϑ < 1 gibt es zwei zueinander konjugiert komplexe Lösungen

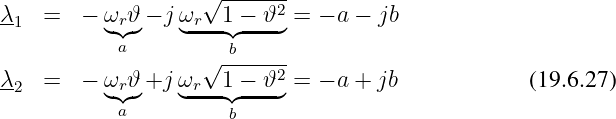
√ ------- λ1 = − ωrϑ|− j ωr--1 −-ϑ2 = − a − jb ◟◝◜a◞ ◟ ◝b◜ ◞ √ -----2- λ2 = − ω◟r◝ϑ◜◞+j ω◟r---1◝ −◜-ϑ-◞= − a + jb (19.6.27) a b

die zu einer gedämpften Schwingung führen

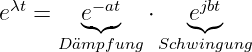λt −at jbt e = e◟◝◜◞ ⋅ e◟◝◜◞ D¨ampfung Schwingung

(19.6.28)

Eingesetzt in die Lösung der homogenen DGL wird

if = [K1 cos(bt) + K2 sin(bt)]e−at

(19.6.29)

Mit der Eigenkreisfrequenz des Schwingkreises¹¹

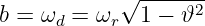√ ------- b = ωd = ωr 1 − ϑ2

(19.6.30)

Aus dem stetigen Spulenstrom (Gln. 19.6.12) ergibt die erste Gleichung zur Bestimmung der Konstanten

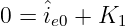0 = ˆie0 + K1

(19.6.31)

Für die stetige Kondensatorspannung (Gln. 19.6.15) benötigen wir wieder die Ableitung des flüchtigen Stromanteils. Mit dessen Ableitung

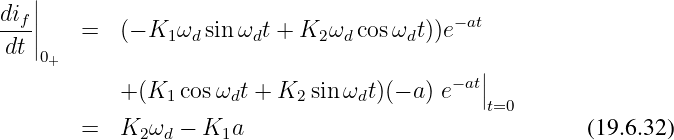
di || --f|| = (− K1 ωdsinωdt + K2 ωd cosωdt))e−at dt |0+ −at|| + (K1 cosωdt + K2 sin ωdt)(− a) e |t=0 = K2 ωd − K1a (19.6.32)

erhalten wir die zweite Bestimmungsgleichung zu

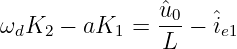ˆu0 ωdK2 − aK1 = ---− ˆie1 L

(19.6.33)

Die beiden Konstanten werden damit

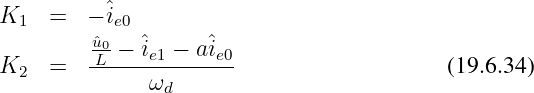
K1 = − ˆie0 ˆu0 ˆ ˆ K = L-−--ie1-−-aie0 (19.6.34) 2 ωd

6. Berechnung:

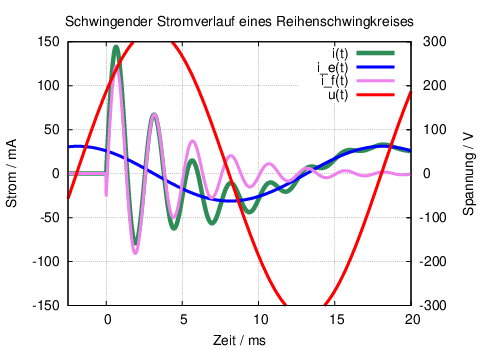
Die nachfolgenden Grafiken zeigen den Stromverlauf beim Einschalten eines RLC-Reihenschwingkreises an eine Wechselspannung (Frohne u. a., 2005, Seite 426) mit den konstante Werten û = 325 V, φ_u = 35∘, f = 50 Hz, L = 0,525 H, C = 0,3 µF und verändertem Widerstand R (siehe Tab. 19.1) für die drei Fälle¹².

Fall	R∕Ω	ϑ	K₁∕A	K₂∕A	f_d∕Hz

1	3600	1,36	−0,07025	0,04195
2	2640	1,00	−0,02822	287,783
3	250	0,09	−0,02592	0,14136	399,24

Tabelle 19.1: Parameter der an Wechselspannung geschalteten RLC-Schaltung

Fall 1:

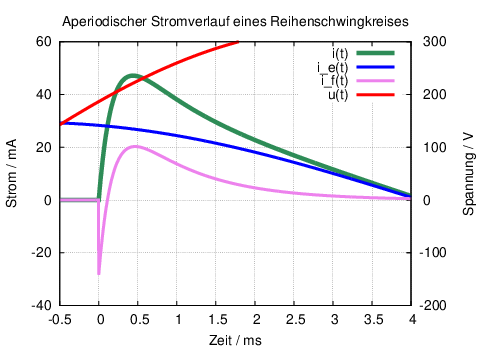
Im aperiodischen Fall verläuft der Strom beim Einschalten einer Wechselspannung an den RLC-Kreis entsprechend Abb. 19.6.2 ohne Schwingung gedämpft durch den ohmschen Widerstand.

Abbildung 19.6.2: Aperiodischer Stromverlauf beim Einschalten einer Wechselspannung

Fall 2:

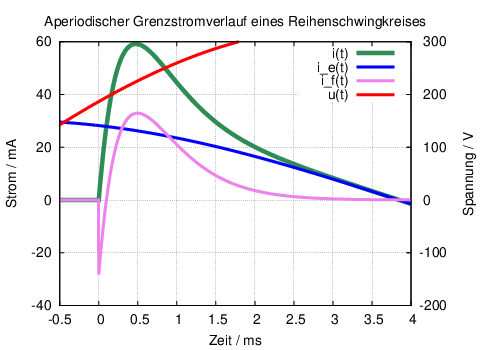
Im aperiodischen Grenzfall verläuft der Strom beim Einschalten einer Wechselspannung an den RLC-Kreis entsprechend Abb. 19.6.3 ebenfalls ohne Schwingung gedämpft, aber mit der kürzest möglichen Einschwingzeit.

Abbildung 19.6.3: Aperiodischer Grenzfall des Stromverlaufs beim Einschalten einer Wechselspannung

Fall 3:

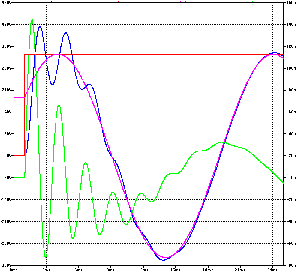
Im periodischen Fall verläuft der Strom beim Einschalten einer Wechselspannung an den RLC-Kreis entsprechend Abb. 19.6.3 mit einer Schwingung, bis er den stationären Zustand erreicht hat.

Abbildung 19.6.4: Periodischer Stromverlauf beim Einschalten einer Wechselspannung

⁷Schaltung mit R = 250Ω, LTspice-Simulation mit grün: i, blau u_C, violett: u und rot: Schalten

⁸Aufgrund der zweiten Ableitung spricht man von einer DGL 2. Ordnung. Für eine RLC-Parallelschaltung an einer Stromquelle würde man die DGL als Funktion der Kondensatorspannung aufstellen.

⁹pq-Formel

¹⁰Für den Strom i_L = i_e + i_f bleibt die Ableitung î_e1 gleich. Ableitung für i_f = f₁(t) ⋅ f₂(t) mit mit der Produktregel: i′_f = K₂e^λt + (K₁ + K₂t)λe^λt

¹¹Schwingung ohne peridische äußere Erregung

¹²f_d ist die Eigenfrequenz des Schwingkreises

[next] [prev] [prev-tail] [front] [up]