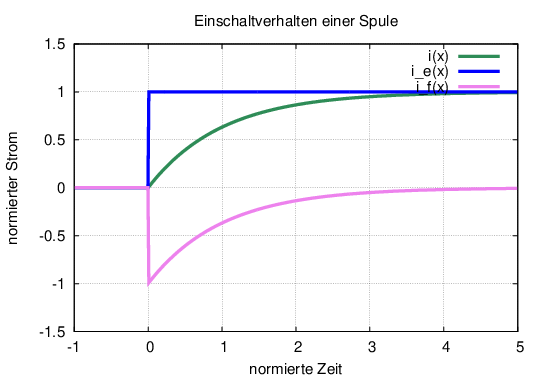
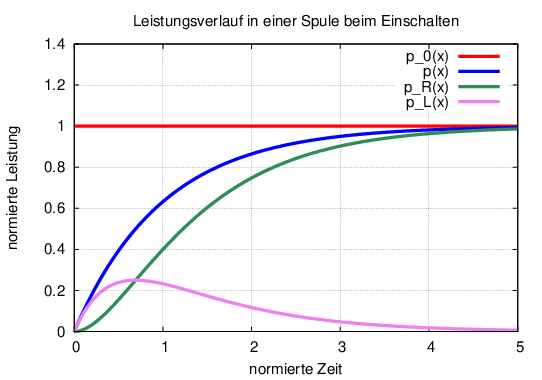
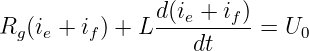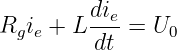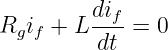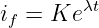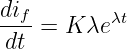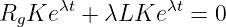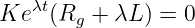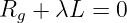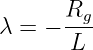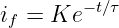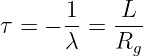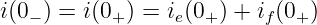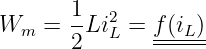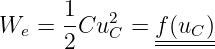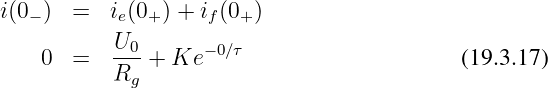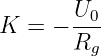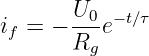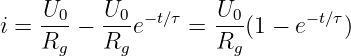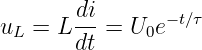Exponentialansatz

[next] [prev] [prev-tail] [tail] [up]

19.3 Exponentialansatz

Beispiel:

Ein Schalter verbindet eine reale Spule mit einer realen Gleichspannungsquelle, wie in Abb. 19.3.1 zu sehen ist.

t < 0:

I = 0

t = 0:

Schaltvorgang

i = f(t) = I_e+?

t ≫ 0:

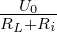
I_e = --U0--
RL+Ri

Abbildung 19.3.1: Beispiel eines Schaltvorganges

2. Netzwerkber.:

Für die Spule aus Abb. 19.3.1 ergibt sich aus der Maschenregel für die Augenblickswerte der Spannungen

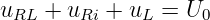uRL + uRi + uL = U0

(19.3.1)

mit den bekannten Bauelementegleichungen die DGL mit konstanten Koeffizienten

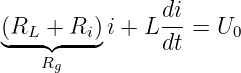di (RL + Ri)i + L-- = U0 ◟---◝◜---◞ dt Rg

(19.3.2)

Lösung:

Da es sich um ein Gleichstromnetz handelt, wird direkt

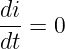di -- = 0 dt

(19.3.3)

und somit der eingeschwungene Strom zu

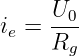i = U0- e Rg

(19.3.4)

Mathematik:

Die Zerlegung des Ausgleichsvorgangs entspricht der Lösung der inhomogenen Differentialgleichung mit konstanten Koeffizienten

Eingeschwungener Zustand:
→Partikuläre Lösung der inhomogenen DGL
Übergangsvorgang:
→ Allgemeine Lösung der homogenen DGL mit Konstantenbestimmung

Speziell:

Bei homogener DGL ist die Störfunktion (Spannungsquelle U₀) Null, so dass nur ein Übergangsvorgang existiert.

19.3.1 Homogene DGL

1. DGL:

Die DGL für den Übergangsvorgang bekommt man wie beim eingeschwungenen Zustand aus der Netzwerkanalyse im Zeitbereich. Für den Ausgleichsvorgang nach dem Einschalten einer Gleichspannung an eine Spule entsprechend Abb. 19.3.1 ergibt sich die DGL in Gln. 19.3.2. Setzt man den Ausgleichsstrom aus zwei Anteilen i = i_e + i_f in die DGL ein, so erhält man

R (i + i ) + L d(ie-+-if)= U g e f dt 0

(19.3.5)

Stationär:

Dieselbe DGL ergibt sich natürlich auch für den eingeschwungenen Zustand, im Prinzip für t →∞, wenn also der flüchtige Strom zu Null geworden ist

di Rgie + L -e-= U0 dt

(19.3.6)

Flüchtig:

Durch Subtraktion dieser DGL entsprechend der Summenregel der Differentialrechnung erhält man für den Übergangsvorgang die homogene DGL zu

di Rgif + L --f = 0 dt

(19.3.7)

Formal:

Wird in der DGL für den Ausgleichsvorgang die Störfunktion Null gesetzt, so erhält man die homogene DGL des Übergangsvorgangs dadurch, dass der Index f ergänzt wird.

Lösung:

Mit Hilfe der Mathematik sind folgende Lösungsmethoden für homogene DGLs mit konstanten Koeffizienten möglich:

Bei DGLs erster Ordnung kann die Trennung der Variablen verwendet werden, die aber gegenüber der 2. Methode keine Vorteile hat → Ergebnis e-Funktion.
Lösung durch den e^λt-Ansatz für DGLs beliebiger Ordnung.

3. Hom. DGL:

Die DGL der Spule war 1. Ordnung, daher wählt man den Ansatz

if = Ke λt

(19.3.8)

Nach der Differentiation ergibt sich

dif λt dt = K λe

(19.3.9)

DGL:

In die homogene DGL eingesetzt wird daraus

λt λt RgKe + λLKe = 0

(19.3.10)

Umsortieren ergibt

Ke λt(Rg + λL ) = 0

(19.3.11)

K = 0 ergibt keinen flüchtigen Strom, e^λt kann nicht Null werden, also muss

Rg + λL = 0

(19.3.12)

sein und damit wird

R λ = − --g L

(19.3.13)

Lösung:

Damit lautet die allgemeine Lösung der homogenen DGL

if = Ke −t∕τ

(19.3.14)

mit der Zeitkonstanten τ, der charakteristischen Größe des Ausgleichsvorganges

τ = − 1-= -L- λ Rg

(19.3.15)

19.3.2 Inhomogene DGL

Konstanten:

Die Bestimmung der Konstanten entsprechend der Ordnung der DGL erfolgt aufgrund der stetigen Anfangsbedingungen der Zustandsgrößen

i(0 ) = i(0 ) = i (0 ) + i(0 ) − + e + f +

(19.3.16)

Mathematik:

Mathematisch sind der linksseitige Grenzwert und der rechtsseitige zum Zeitpunkt t = 0 identisch. Sprungartige Änderungen der Zustandsgrößen sind elektrotechnisch nicht möglich, weil

bei einer Spule deren magnetische Energie $W = 1-Li2 = f(i ) m 2 L ---L--$
und bei einem Kondensatoren dessen elektrische Energie $1 We = --Cu2C = f(uC ) 2 ------$

sich nur stetig ändern können.

4. Konstanten:

Für die Spule ist die Anfangsbedingung entsprechend

i(0 − ) = ie(0+) + if(0+) U0- − 0∕τ 0 = Rg + Ke (19.3.17)

Mit e⁰ = 1 ergibt sich die Konstante zu

K = − U0- Rg

(19.3.18)

Die Lösung der homogenen DGL (allgemeine Lösung) ist damit bestimmt

U0- −t∕τ if = − R e g

(19.3.19)

5. Überlagerung:

Der Ausgleichsvorgang ist die Überlagerung der partikulären Lösung i_e aus Gln. 19.3.4 und der allgemeinen Lösung i_f

U0 U0 U0 i = --- − ---e−t∕τ = ---(1 − e−t∕τ) Rg Rg Rg

(19.3.20)

6. Berechnung:

Der graphische Verlauf in Abb. 19.3.2 mit der normierten Zeitkonstanten τ = L∕R_g = 1s und der normierten Amplitude U₀∕R_g = 1A zeigt den Einfluss der Stromteile i = i_e + i_f.

Abbildung 19.3.2: Stromverlauf in einer Spule beim Einschalten einer Gleichspannung

19.3.3 Ausgleichsvorgang

6. Berechnung:

Mit der Zustandsgröße können weitere Berechnungen erfolgen

Spannung an der Spule

di uL = L -- = U0e− t∕τ dt

(19.3.21)

oder die Gesamtleistung, d.h. die Leistungen im Innenwiderstand R_I der Quelle und im Kupferwiderstand R_L der Spule …

BERECHNUNG:

Grafik:

Die graphische Darstellung zeigt den normierten Leistungsverlauf in einer Spule beim Einschalten einer Gleichspannung mit p₀ = U₀²∕(R_L + R_i) = 1W

Abbildung 19.3.3: Leistungsverlauf in einer Spule beim Einschalten einer Gleichspannung

Verfahren:

Zur Berechnung des Ausgleichsvorganges nach einem Schaltvorgang in elektrischen Netzen mit Gleich- oder Wechselspannungserregung kann folgender Maßen verfahren werden:

Aufstellen der Differentialgleichung ab t = t₀ für die Zustandsgröße
Gleichstrom- oder Wechselstromberechnung zur Bestimmung des eingeschwungenen Zustandes für t →∞
Berechnen des Übergangsvorganges mit dem Exponentialansatz zur Lösung der homogenen DGL
Bestimmung der Konstanten aus den Anfangsbedingungen und Einsetzen in die allgemeine Lösung
Überlagerung des Übergangsvorganges mit dem eingeschwungenen Zustand zum Ausgleichsvorgang
Weitere Berechnungen und graphische Darstellung der Zeitverläufe

→ Die Zahlen im vorigen Abschnitt entsprechen diesen Punkten!

[next] [prev] [prev-tail] [front] [up]