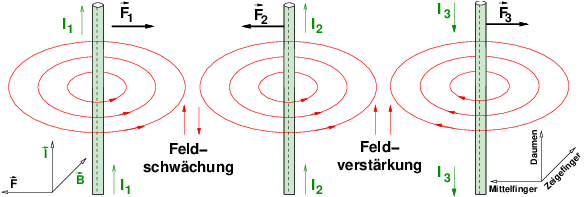
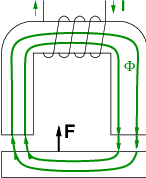
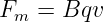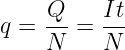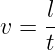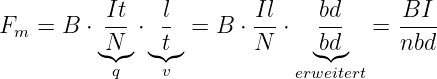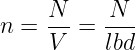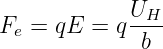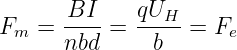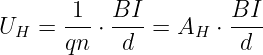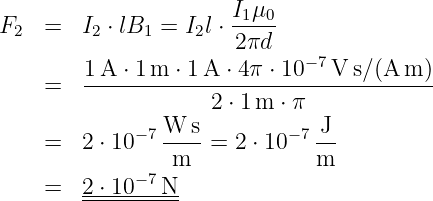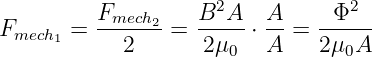Kraft des magnetisches Feldes

[next] [prev] [prev-tail] [tail] [up]

12.8 Kraft des magnetisches Feldes

Kraft:

Es gibt analog zum elektrischen Feld³⁹ beim magnetischen Feld eine Kraftwirkung auf bewegte Ladungen, wie in Abb. 12.8.1 dargestellt .

Abbildung 12.8.1: Kraftwirkung auf einen bewegte Ladungen im Magnetfeld

Mit Gln. 12.1.5 wurde die magnetische Flussdichte genau über diese Kraft, die Lorentzkraft, definiert

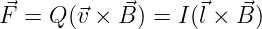
⃗F = Q(⃗v × ⃗B ) = I(⃗l × B⃗)

Die Bewegungsrichtung⁴⁰ positiver Ladungen Q stimmt mit der Definition der technischen Stromrichtung⁴¹ überein.

Leiter:

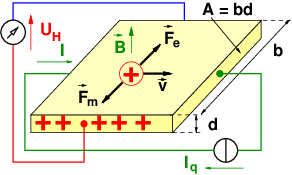
Damit kommt man direkt zur angegebenen Kraftwirkung auf einen stromdurchflossenen Leiter, die senkrecht zur aufgespannten Fläche von Leiter l und magnetischer Flussdichte B ist.

Kreis:

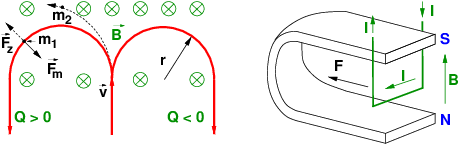
Die Lorentzkraft ändert nur die Bewegungsrichtung⁴² nicht aber den Betrag der Geschwindigkeit.

→ Geladene Teilchen bewegen sich im Magnetfeld auf einer Kreisbahn! Den Radius der Kreisbahn findet man durch ein Kräftegleichgewicht von magnetischer Lorentzkraft

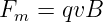F = qvB m

(12.8.1)

und der Zentrifugalkraft

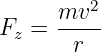2 mv--- Fz = r

(12.8.2)

Frage:

Welche Kraft wirkt denn der Bewegung der Stromschleife im Magneten in Abb. 12.8.1 entgegen?

12.8.1 Halleffekt

Hall:

Eine direkte Anwendung findet sich im Hallsensor⁴³ zur Bestimmung der magnetischen Flussdichte, wie er in Abb. 12.8.2 dargestellt ist .

Abbildung 12.8.2: Halleffekt im p-Halbleiter

Quanten:

Durch den Quanten-Halleffekt, der bei extrem dünnen Leiterplättchen⁴⁴ auftritt kann ein Widerstandsnormal definiert werden⁴⁵

-h -6,626-⋅ 10−34V-A-s2- RH = q2 = (1,602 18 ⋅ 10− 19 A s)2 = 25,812 kΩ

(12.8.3)

das nur von Naturkonstanten abhängt.

Spannung:

Dabei wird die Lorentzkraft

Fm = Bqv

(12.8.4)

auf die Ladung

q = Q--= It- N N

(12.8.5)

die sich mit der Geschwindigkeit

l v = t

(12.8.6)

bewegt, zu

It l Il bd BI Fm = B ⋅ ---⋅ - = B ⋅ ---⋅ --- = ---- ◟N◝◜◞ ◟t◝◜◞ N ◟b◝d◜◞ nbd q v erweitert

(12.8.7)

mit der Konzentration der Ladungsträger

n = N--= N-- V lbd

(12.8.8)

Die entstehende Ladungstrennung baut dann ein elektrisches Gegenfeld auf mit der Kraft

F = qE = qUH-- e b

(12.8.9)

Beide Kräfte heben sich im Gleichgewichtszustand auf

BI-- qUH-- Fm = nbd = b = Fe

(12.8.10)

Daraus ergibt sich die messbare Hallspannung zu

-1- BI- BI- UH = qn ⋅ d = AH ⋅ d

(12.8.11)

Aus den Hallkoeffizienten⁴⁶⁴⁷ des Materials (Paul, 2004, Seite 375) :

n-Halbleiter mit A_H ≈ (−104…−106) ⋅ 10−10 m³∕C
Metalle mit A_H ≈−101 ⋅ 10−10 m³∕C

ergibt sich, dass Hall-Sensoren aus Halbleiterplättchen hergestellt werden.

12.8.2 Kräfte auf Leiter

Leiter:

Wird ein senkrecht zu einem Magnetfeld angeordneter Leiter von einem Strom durchflossen, so überlagert sich das vom Strom erzeugte Magnetfeld mit dem vorhandenen, wie in Abb. 12.8.3 dargestellt, und es wirkt eine Kraft auf den Leiter mit dem Bestreben, den ungestörten Feldverlauf wieder herzustellen.

Abbildung 12.8.3: Feldschwächung und -verstärkung bei einem Leiter im Magnetfeld

→ Aus dem gleichen Grund ziehen sich Leiter mit parallelen Strömen an und stoßen sich ab bei entgegengesetzten Strömen.

Frage:

Ist das wirklich so? Kann man das sehen?

Beispiel 12.8.1 (3 Leiter)

Gegeben seien 3 parallele Leiter in Abb. 12.8.4 in einem Abstand von jeweils d = 1 m, die jeder von einem Strom I₁ = I₂ = I₃ = 1 A durchflossen werden.

Abbildung 12.8.4: Beispiel Kraft auf stromdurchflossene Leiter

Welche Kraft über die Leiter 1 und 2 je Meter Länge aufeinander aus?⁴⁸
Welche Kraft über die Leiter 2 und 3 je Meter Länge aufeinander aus?

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Lorentzkraft Leiter 1 auf Leiter 2 anziehend
$F = I ⋅ lB = I l ⋅ I1μ0 2 2 1 2 2πd 1A ⋅ 1 m ⋅ 1 A ⋅ 4π ⋅ 10 −7V s∕(A m ) = ---------------------------------- 2 ⋅ 1 m ⋅ π = 2 ⋅ 10− 7 W-s = 2 ⋅ 10−7 J m m = 2-⋅ 10−-7N$
Lorentzkraft Leiter 2 auf Leiter 3: abstoßend

12.8.3 Kräfte an Grenzflächen

Kraft:

Die Kraft F in einem magnetischen Kreis ist so gerichtet, dass bei konstanter elektrischer Durchflutung Θ der magnetische Fluss Φ möglichst groß wird.

----Vm------ ! Φ = R + R = const. mL mE RmL = f (lL) Vm = Θ = N I I = f (lL)

Abbildung 12.8.5: Anziehungskraft eines Magneten auf Eisen

Ansatz:

Bleibt der magnetische Fluss Φ konstant und damit auch die magnetische Induktion B so ändert sich durch die Änderung der Luftspaltlänge in Abb.12.8.5 nur die im Volumen des Luftspalts V _Luft gespeicherte magnetische Energie W_Luft⁴⁹.

Wichtig:

Nach dem magnetischen Maschensatz (Gln. 12.5.8) muss sich bei einer Verkleinerung des magnetischen Widerstandes im Luftspalt aufgrund einer kürzeren Luftspaltlänge natürlich die magnetische Erregung der Quelle Θ über den Spulenstrom reduzieren, damit der magnetische Fluss Φ konstant bleibt.

Energie:

Die zur Bewegung der Gegenplatte aufzubringende mechanischen Energie

dWmech = F ⋅ dl

(12.8.12)

ist gleich der Änderung der magnetischen Energie dW_mag wobei mit B = const. auch die Energiedichte nach Gln. 12.7.7

2 w = 1-⋅ B- 2 μ

konstant bleibt und sich nur das Volumen des Luftspalts insgesamt auf beiden Seiten um

dV = 2 ⋅ Adl

(12.8.13)

ändert und somit wird

B2 dWmag = w ⋅ dV = ----⋅ 2Adl 2μ0

(12.8.14)

Kraft:

Durch Gleichsetzen der Energieänderungen

2 dWmech = Fmech2 ⋅ dl =-B--⋅ 2Adl = dWmag 2μ0

(12.8.15)

ergibt sich die Kraft auf beide Seiten des Luftspalts zu

2 Fmech2 = B-A-- μ0

(12.8.16)

und somit die Kraft auf eine Seite des Luftspalts zu

Fmech2- B2A-- A- -Φ2--- Fmech1 = 2 = 2μ ⋅A = 2μ A 0 0

(12.8.17)

Frage:

Kann man diese Herleitung auch beim Kondensator verwenden?⁵⁰

Lösung:: Die Anwort ist: Ja. Die Lösung wird in der Vorlesung erarbeitet.

³⁹Kraft auf ruhende Ladungen

⁴⁰Dreht man den 1. Vektor v mit einer Rechtsschraube auf dem kürzesten Weg auf den 2. Vektor B dann dreht sich die Schraube in Richtung von F = Q(v ×B).

⁴¹Wird eine negative Ladung im Magnetfeld bewegt, so ergibt sich eine negative Lorentzkraft, d.h. die Richtung der Kraft auf negative Ladungen ist entgegengesetzt zu der auf positive Ladungen.

⁴²Für positive Ladungen entsprechend der Rechte-Hand-Regel: Rechtwinkliges Koordinatensystem mit Daumen in Richtung v, Zeigefinger in Richtung B und Mittelfinger in Richtung F

⁴³benannt nach dem amerikanischen Physiker E. Hall, 1855 - 1938

⁴⁴Dicke der Inversionsschicht im MOSFET, einige nm

⁴⁵Mit dem plankschen Wirkungsquantum [h] = Js = W s² = V As², das Teilchen- und Welleneigenschaften eines Photons verknüpft.

⁴⁶Sie werden auch Hall-Konstanten genannt und machmal mit dem Formelzeichen R_H versehen, das aber eine leichte Verwechslung mit dem Hall-Widerstand ergibt.

⁴⁷Zu Ehren von E. Hall, 1855 – 1938, amerikanischer Physiker.

⁴⁸Überlegen Sie einmal ergänzend, ob der Leiter 3 auch eine Kraft auf den Leiter 1 ausübt! Erzeugt der Leiter 3 am Ort des Leiters 1 ein Magnetfeld?

⁴⁹und die im Eisenkern gespeicherte magneteische Energie W_Eisen = V _EisenB²∕2μ bleibt konstant

⁵⁰Es handelt es sich bei dieser Aufgabe um eine typische Transferleistung, bei der Sie erworbenen Wissen auf andere Themen übertragen sollen.

[next] [prev] [prev-tail] [front] [up]