12.1 Magnetische Wirkung des elektrischen Stroms

Frage:

Was macht ein magnetisches Feld²?

Antwort:

Es übt Kraft auf bewegte Ladungen (Ströme³) aus!

---

Abbildung 12.1.1: Transformator und Relais

---

Experiment:

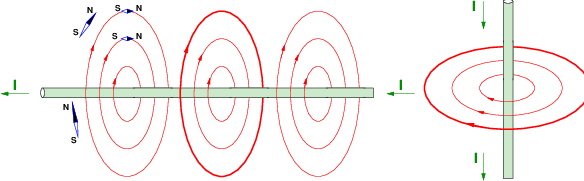
Eine Magnetnadel wird wie in Abb. 12.1.2 in der Nähe eines stromdurchflossenen Leiters abgelenkt. Führt man die Magnetnadel um den Leiter herum, so zeigt sich, dass er von kreisförmigen und geschlossenen Magnetlinien umgeben ist, deren Richtung im Sinne einer Rechtsschraube⁴ zugeordnet ist.

---

Abbildung 12.1.2: Magnetfeld um einen geraden Leiter

---

→ Die Stärke des Magnetfeldes und damit die Dichte der Kraftlinien ist proportional dem Strom durch den Leiter.

Spule:

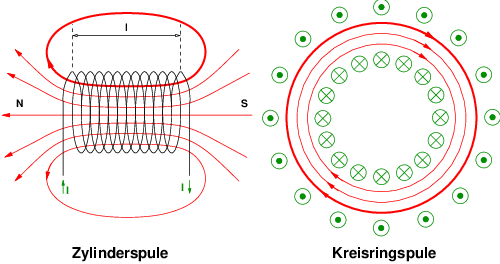
Um ein stärkeres Magnetfeld zu erzeugen, kann man den Leiter zu einer Spule verbiegen, bei dem der Leiter dasselbe Raumstück mehr als einmal durchläuft. In Abb. 12.1.3 sind die Magnetfelder einer Zylinderspule und einer Ringspule dargestellt.

---

Abbildung 12.1.3: Magnetfeld in einer Zylinder- und Ringspule

---

→ Das Magnetfeld im Inneren einer Zylinderspule ist homogen⁵. Bei einer Ringspule gibt es nur das homogene Magnetfeld im Inneren der Spule.

Ein Magnetfeld ist die Voraussetzung für die Umwandlung von elektrischer Leistung in mechanische und umgekehrt. Neben dem Motor wird dieses Prinzip auch beim Relais angewendet. Beim Transformator wird ein veränderliches Magnetfeld zur Transformation von Wechselspannungen und -strömen benötigt, also Begriffe, die erst im späteren Verlauf behandelt werden, die dann aber sicher verstanden werden können, wenn die aktuellen Grundlagen verstanden worden sind.

Kraft:

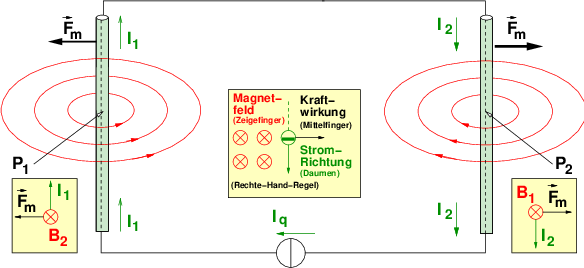
Im Stromkreis mit parallelen Leiterstücken wie in Abb. 12.1.4 verursacht der Strom I₁ ein Magnetfeld am Ort P₂, das eine Kraft⁶ auf die bewegte Ladung als Strom I₂ ausübt.

---

Abbildung 12.1.4: Kraft auf einen Leiter im Magnetfeld eines anderen Leiters

---

→ Umgekehrt für Strom I₂ gültig! Beide Kräfte addieren sich und drücken die Leiter auseinander.

Ladung:

Die Ladung Q braucht mit der Geschwindigkeit v die Zeit t um den Leiter mit der Länge l zu durchfließen. Mit der Proportionalitätskonstanten μ₀ wird die (experimentelle) Kraft dann zu

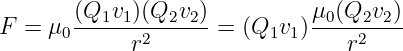(12.1.1)

Das Produkt aus Ladung und Geschwindigkeit wird zum Produkt aus Strom und Leiterlänge mit

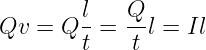(12.1.2)

Flussdichte:

Wir führen zur Erfassung des Magnetfeldes des Leiters 2 die Flussdichte⁷

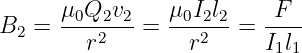(12.1.3)

ein und erhalten den Betrag der Kraft auf bewegte Ladungen im Leiter 1 durch das Magnetfeld des Leiters 2 zu

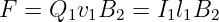(12.1.4)

Lorentz:

Die Richtung der experimentell festgestellten Kraft lässt sich mathematisch mit dem Vektorprodukt erfassen⁸

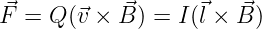(12.1.5)

wobei die Ladungen Q mit der Geschwindigkeit v das gerichtete Leiterstück der Länge l im Magnetfeld B durchlaufen⁹.

→ Diese Kraft auf bewegte Ladungen heißt Lorentzkraft.

Motor:

Für den Betrag der Lorentzkraft erhalten wir mit dem Winkel φ zwischen l und B aus dem Vektorprodukt direkt

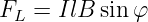(12.1.6)

→ Dieses ist die Grundgleichung der elektrischen Motoren, mit denen über den Umweg des magnetischen Feldes elektrische in mechanische Energie umgewandelt werden kann.

→ Beim Generator wirkt das Prinzip genau umgekehrt — es wird aber später mit dem Induktionsgesetz beschrieben.