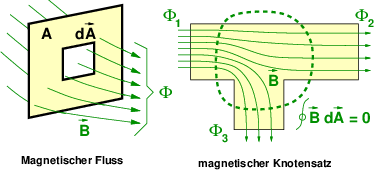
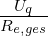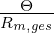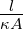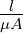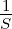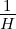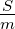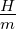Magnetischer Kreis

12.5 Magnetischer Kreis

Anschaulich:

Je mehr Magnetlinien senkrecht durch eine Querschnittsfläche wie in Abb. 12.5.1 hindurch treten, um so größer ist die magnetische Induktion B.

Abbildung 12.5.1: Magnetischer Fluss und magnetischer Knotensatz

Fluss:

Die Gesamtzahl der Magnetlinien, die in einem bestimmten Raumgebiet vorhanden sind, wird als magnetischer Fluss Φ definiert

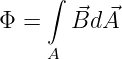∫ Φ = ⃗BdA⃗ A

(12.5.1)

→ Damit erklärt sich auch die Flussdichte B = Φ∕A!

Einheit:

Die Einheit des magnetischen Flusses ist Weber²⁷

2 [Φ ] = [B ] ⋅ [A] = T m = V s = Wb

(12.5.2)

Quellen:

Wie der elektrische Strom ist auch der magnetische Fluss quellenfrei. An keiner Stelle des Raumes verschwinden oder entstehen Feldlinien. Für eine geschlossene Hüllfläche ergibt das den magnetischen Knotensatz

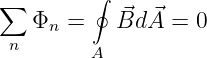∮ ∑ Φ = ⃗Bd ⃗A = 0 n n A

(12.5.3)

→ Anstelle des elektrischen Leiters wird der magnetische Knotensatz auf einem magnetischen Leiter, z.B. den Eisenkern eines Transformators wie in Abb. 12.5.1 angewendet.

Stetig:

Wie der elektrische Strom ist auch der magnetische Fluss stetig. Die Feldlinien sind in sich geschlossen. Φ ist stetig in verschiedenen Materialien.

→ Die magnetische Induktion B = Φ∕A ist nur bei gleicher Fläche A und die magnetische Feldstärke H = B∕μ nur bei gleicher magnetischer Leitfähigkeit (μ) stetig.

Vergleich:

Vergleichen wir die Definition des magnetischen Flusses nach Gln. 12.5.1

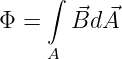
∫ Φ = ⃗BdA⃗ A

mit der Definition des elektrischen Stromes

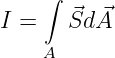
∫ I = S⃗d A⃗ A

so können wir einen analogen Übergang von Feldgrößen zu Integralgrößen auch beim magnetischen Feld durchführen.

Spannung:

Analog zur Integralgröße der elektrischen Spannung

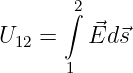
∫2 U12 = ⃗Ed ⃗s 1

wird die Integralgröße der magnetischen Spannung definiert zu

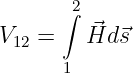2 ∫ V12 = H⃗d ⃗s 1

(12.5.4)

Einheit:

Die Einheit der magnetischen Spannung ist Ampere.

[V ] = A

(12.5.5)

Homogen:

Für ein homogenes Magnetfeld gilt dann

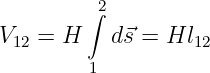∫2 V12 = H d⃗s = Hl12 1

(12.5.6)

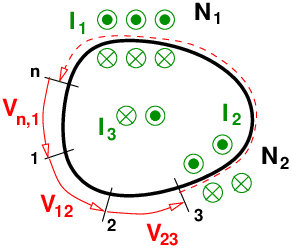
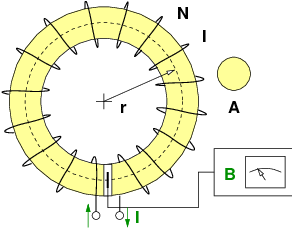
→ Die magnetische Spannung ist i.a. vom Integrationsweg abhängig²⁸, insbesondere gehen umschlossene Ströme ein, wie in Abb. 12.5.2 zu sehen ist .

Abbildung 12.5.2: Magnetischer Maschensatz bei 3 Spulen

Masche:

In Analogie zum elektrischen Feld kann auch ein magnetischer Maschensatz eingeführt werden. Ausgehend vom Durchflutungssatz in Gln. 12.3.1 erhält man mit den magnetischen Spannungen

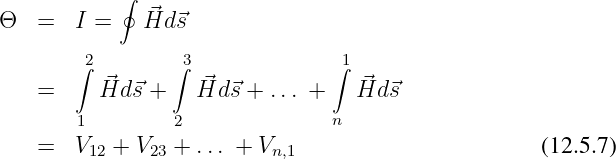
∮ Θ = I = ⃗Hd ⃗s 2∫ ∫3 ∫1 = ⃗Hd ⃗s + ⃗Hd ⃗s + ... + H⃗d ⃗s 1 2 n = V + V + ... + V (12.5.7) 12 23 n,1

den magnetischen Maschensatz zu²⁹

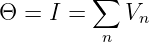∑ Θ = I = Vn n

(12.5.8)

Widerstand:

Analog zum elektrischen Widerstand R_e = U∕I kann auch ein magnetischer Widerstand definiert werden

R = V- m Φ

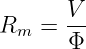(12.5.9)

Einheit:

Die Einheit des magnetischen Widerstandes ist

[V-] -A-- A-- -1 [Rm ] = [Φ ] = Wb = V s = H

(12.5.10)

Homogen:

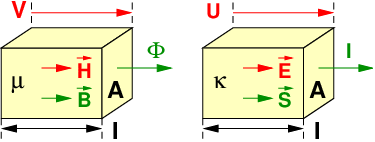
Speziell im homogenen Magnetfeld erhalten wir mit

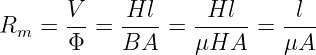R = V-= Hl--= -Hl---= --l- m Φ BA μHA μA

(12.5.11)

eine vollkommen analoge Berechnungsgleichung zum elektrischen Widerstand im homogenen Feld wie auch aus Abb. 12.5.3 zu sehen ist

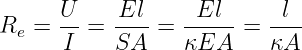Re = U-= El--= -El--= -l- I SA κEA κA

(12.5.12)

Abbildung 12.5.3: Analogie magnetischer und elektrischer Widerstand

Kreis:

Die Berechnung eines magnetischen Kreises kann mit den Verfahren der Gleichstromtechnik wie die eines elektrischen Kreises durchgeführt werden. Eine Zusammenstellung der Analogie zwischen elektrischen und magnetischen Kreis ist in Tab. 12.1 gegeben.

→ Damit gelten natürlich auch das Ohmsche Gesetz und die Kirchhoffschen Gleichungen.

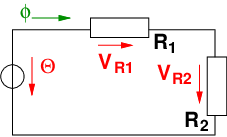
	Elektrischer Kreis	Magnetischer Kreis

Schaltung


Ursache	elektrische Spannung	magnetische Spannung
	U_q	Θ = NI

Wirkung	elektrischer Strom	magnetischer Fluss
	I =	Φ =

Ohmsches	U = R_eI	V = R_mΦ
Gesetz	[U] = V	[V ] = A

Widerstand	R_e =	R_m =
Einheit	[R_e] =	[R_m] =

Material-	κ	μ = μ_rμ₀
eigenschaft	[κ] =	[μ] =


Knoten
gleichung	∑ _nI_n = 0	∑ _nΦ_n = 0

Maschen
gleichung	∑ _nU_n − U_q = 0	∑ _nV _n − Θ = 0

Tabelle 12.1: Vergleich von elektrischem und magnetischem Kreis

Nichtlinear:

Voraussetzung zur vereinfachten Berechnung magnetischer Kreise sind lineare magnetische Widerstände.

→ Mit einer nichtlinearen B-H-Magnetisierungskurve von Eisen muss dann unter Umständen mit nichtlinearen Bauelementen gerechnet werden.

Bemerkung:

Wer möchte noch einen Nobelpreis bekommen? Es gelten die Materialgleichungen μ = μ_rμ₀ und ϵ = ϵ_rϵ₀.

→ Wer findet das κ_r für κ = κ_rκ₀?

Beispiel 12.5.1 (Magnetischer Kreis)

Gegeben sei eine Kreisringspule (siehe Abb. 12.5.4) mit den Daten: Luftspaltlänge l_L = 1 mm, Eisenlänge l_E = 10 cm, relative Permeabilität in Eisen μ_r = 1000, Querschnittsfläche des Eisens A = 10 cm², Windungszahl N = 100.

Abbildung 12.5.4: Beispiel zur Kreisringspule

Bei der dargestellten Kreisringspule ist der magnetische Fluss Φ für einen Strom I = 1 A zu berechnen.
Wie lang muss die Eisenlänge sein, damit der magnetische Widerstand des Eisens gleich dem des Luftspalts ist?

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Magnetischer Fluss
$Θ N I ⋅ A μ0 Φ = ------------= -----lE-- RmL + RmE ll + μr 100 ⋅ 1A ⋅ 10 cm2 ⋅ 4π ⋅ 10−7V s∕(A m ) = ------------------------------------- 0,1cm + 0,01 cm = 0,114-⋅ 10−-3V-s ---------------$
Länge Eisenwiderstand $lE = μrlL = 1000 ⋅ 1mm = 1m--$

²⁷Zu Ehren von Wilhelm Eduart Weber, 1804 – 1891, deutscher Physiker, stellte die Theorie des Magnetismus auf.

²⁸Entsprechend dem Durchflutungssatz ∮ Hds = ∑ _nI_n = Θ aus Gln. 12.3.1 und damit anders als die elektrische Spannung!

²⁹Anders als im geshlossenen elektrischen Kreis mit ∑ _nU_n = 0.

[next] [prev] [prev-tail] [front] [up]