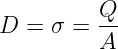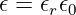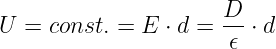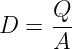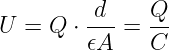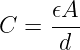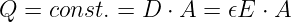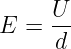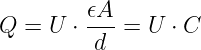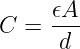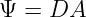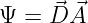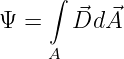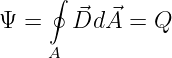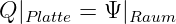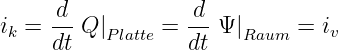-
Wirkung:
-
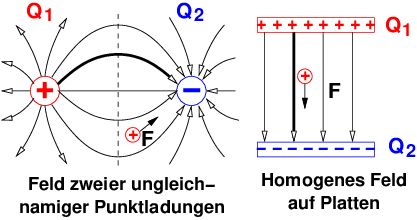
Die Kraftwirkung von Ladungen aufeinander in einem Raum,
wie in Abb. 10.2.1 zu sehen, wird mit der elektrischen
Feldstärke beschrieben.
-
Definition:
-
Die elektrische Feldstärke in jedem Raumpunkt
ist analog zur Kraft F = QE ein Vektor, der von der positiven zur
negativen Ladung gerichtet ist.
-
Einheit:
-
Die Einheit der elektrischen Feldstärke ist V/m. Wieso?
-
Arbeit:
-
Zur Bewegung einer Ladung von Punkt 1 nach 2 in einem elektrischen
Feld ist eine Arbeit notwendig, die sich aus dem Produkt der auf
zuwendenden Kraft entlang des Weges ergibt, integral also
→ Zur Bewegung einer positiven Ladung in Richtung der Feldlinien
ist keine Arbeit notwendig (Minuszeichen!), sondern man kann
die im Feld gespeicherte Energie zum Bewegen der Ladung
verwenden.
-
Beispiele:
-
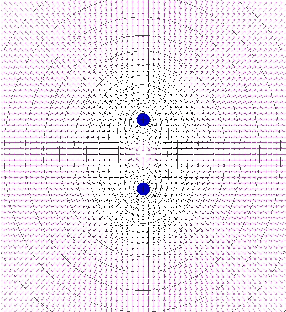
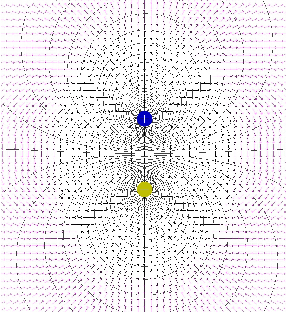
Die elektrischen Feldbilder einer Doppelladung und eines
Dipols,
wie in Abb. 10.2.2 zu sehen, können mit einem
Java-Applet
erzeugt werden.
-
Definition:
-
Durch Normierung der auf zuwendenden Arbeit W auf die zu
bewegende Ladung Q erhält man die Spannung
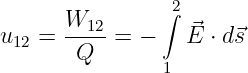 | (10.2.4) |
mit der Einheit Volt
![[U ] = [W-] = W--s = V-A- = V
[Q ] A s A](gde_330x.png) | (10.2.5) |
-
Frage:
-
Wann ist das Skalarprodukt
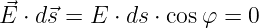 | (10.2.6) |
→ Wenn entweder E = 0 ist oder ds = 0 oder E⊥ds ist.
-
Spannung:
-
Die elektrische Spannung u12 zwischen den Raumpunkten 1 und 2 ist
gleich dem Wegintegral der elektrischen Feldstärke zwischen diesen
Punkten.
-
Eigenschaft:
-
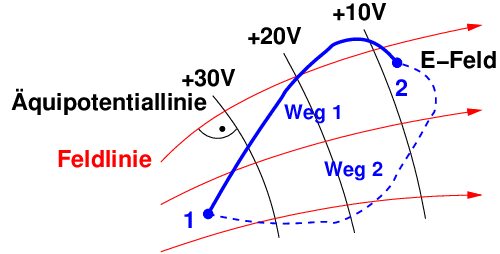
Das Wegintegral der elektrischen Feldstärke zwischen den Punkten 1
und 2 wie in Abb. 10.2.3 ist wegunabhängig!
→ Wäre dem nicht so, so bliebe auf einem geschlossenen
Weg von 1 nach 2 und dann zurück von 2 nach 1 eine
bestimmte Arbeit übrig und wir hätten ein Perpetuum
Mobile.
-
Bezug:
-
Die Definition der Spannung erfordert zwei Punkte in einem
elektrischen Feldstärkefeld.
→ Definiert
man alle Spannungen in einem Feldstärkefeld gegenüber einem
beliebigen, festen Referenz- oder Bezugspunkt, so spricht man
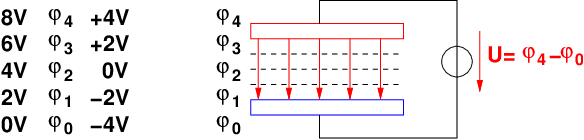
von dem Potential eines Punktes (siehe Abb. 10.2.4) .
-
Definition:
-
Der Bezugspunkt bekommt elektrotechnisch den Wert φ0 = 0V . Aus
der Definition der Spannung in Gln. 10.2.4 erhalten wir das Potential
eines Punktes im Feld zu
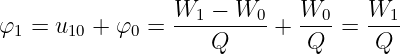 | (10.2.7) |
-
Skalar:
-
Das elektrische Potential φ ist die der potenziellen Energie W einer
Ladung an einem Ort zugeordnete skalare Größe.
→ Damit ist sich die Spannung zwischen zwei Punkten gleich der
Differenz der Potentiale der Punkte
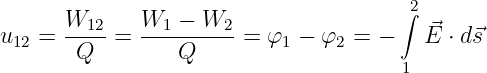 | (10.2.8) |
-
Eigenschaften:
-
- Dem Potentialfeld kann analog zur potenziellen Energie
im Schwerkraftfeld (Normal-Null) ein beliebiger
Bezugspunkt (meist Masse-Potential) zugeordnet
werden.
- Die Spannung zwischen zwei Punkten bleibt stets gleich,
unabhängig von der Wahl des Bezugspunktes.
- Das Potential sinkt stets in Feldrichtung. Aus dem Potential
berechnet sich der elektrische Feldstärkevektor zu
![[ ]
⃗E(x,y,z) = − grad φ = − ∂φ-, ∂-φ, ∂-φ
∂x ∂y ∂z](gde_336x.png) | (10.2.9) |
-
Exkurs:
-
Mit einem kleinen mathematischen Exkurs kann man aus der
bisherigen Differentialform der Feldstärke die mathematischen
Grundlagen der Maxwellschen Gleichungen in Differentialform
legen.
-
Definitionen:
-
Wir definieren den Nabla-Operator
zu
![[ ]
⃗ ∂-- ∂-- ∂--
∇ = ∂x, ∂y, ∂z](gde_337x.png) | (10.2.10) |
Damit wird die Berechnung des Gradienten des Potentialfeldes zu
einer Multiplikation des Nabla-Vektors mit einem Skalar → Skalare
Multiplikation
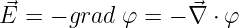 | (10.2.11) |
-
Maxwell:
-
Maxwell baute seine Theorie der elektromagnetichen Wellen auf den
4 Maxwellschen Gleichungen auf, indem er zeigte, dass diese
Gleichungen Lösungen besitzen, die elektromagnetiche Wellen
beschreiben.
-
4. Gleichung:
-
(Gaußscher Satz, Gln. 10.2.35) Elektrische Ladungen sind
Quellen und Senken des elektrischen Feldes (D = ϵE) →
Skalarprodukt
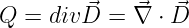 | (10.2.12) |
-
2. Gleichung:
-
(Induktionsgesetz, Gln. 13.1.1) zeitveränderliche magnetische Felder
erzeugen elektrische Wirbelfelder mit in sich geschlossenen
Feldlinien → Vektorprodukt
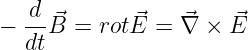 | (10.2.13) |
-
3. Gleichung:
-
Es gibt keine magnetischen Quellen und Senken (sondern nur ein
magnetisches Wirbelfeld)
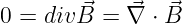 | (10.2.14) |
-
1. Gleichung:
-
(Durchflutungsgesetz, Gln. 12.3.1) Zeitveränderliche elektrische Felder
und stromdurchflossene Leiter (Stromdichte J) erzeugen magnetische
Wirbelfelder
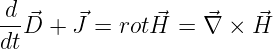 | (10.2.15) |
-
Fläche:
-
Verbindet man Punkte gleichen Potentials miteinander so erhält man
Äquipontentialflächen mit Δu = ∫
E ⋅ ds = 0. Für E≠0 und ds≠0
muss dann E⊥ds gelten.
→ Feldlinien verlaufen stets senkrecht zu Äquipotentialflächen (z.B.
Leiter)!
-
Leiter:
-
Da Leiter (z.B. Platten eines Kondensators) stets das selbe Potential
haben, sind sie immer auch Äquipontentialflächen.
→ An einer Metallspitze herrscht eine hohe Feldstärke, sichtbar
durch eine große Liniendichte,wie in Abb. 10.2.5, mit
Durchschlagsgefahr!
-
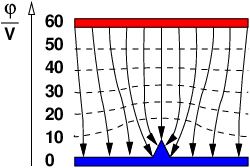
Homogen:
-
Ein elektrisches Feld wird als homogen bezeichnet, wenn die
Feldstärke unabhängig vom Ort überall in Betrag und Richtung gleich
ist (siehe Abb. 10.2.6) .
-
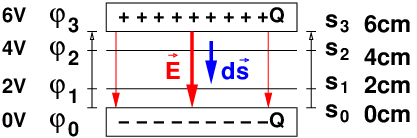
Spannung:
-
Die Berechnung der Spannung nach Gln. 10.2.8 vereinfacht sich in
einem homogenen Feld, wenn der Integrationsweg parallel zum Feld
gewählt wird, wesentlich zu
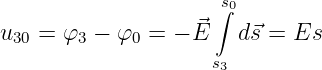 | (10.2.16) |
→ Entsprechend gilt natürlich auch für das Feld
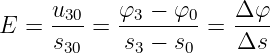 | (10.2.17) |
-
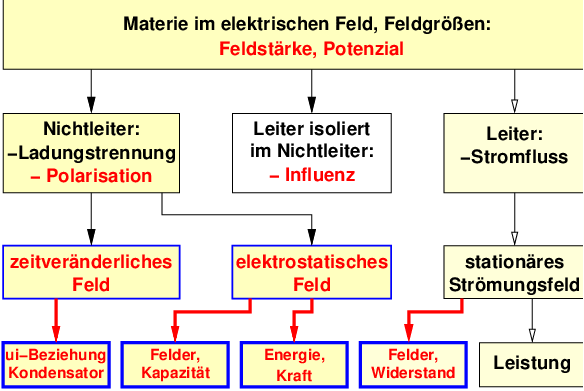
Materie:
-
Eine Kraft wirkt allgemein auf Ladungen,
die sich in Leitern, Halbleitern und
Nichtleitern
im elektrischen Feld befinden. Abb. 10.2.8 zeigt
die typischen Effekte aufgrund der unterschiedlichen
Ladungsträgerbeweglichkeiten.
-
Feldstärke:
-
Die Wirkung der elektrischen Feldstärke nach Gln. 10.2.1 als
Folge der Ladung Q2 auf die Messgröße Q1 entsprechend der
Coulomkraft nach Gln. 10.1.6 muss genauer lauten (Definition der
Messvorschrift)
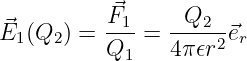 | (10.2.18) |
→ Die Kraft auf die Ladung Q1 im Raum (ϵ) kommt von der Ursache
Q2.
-
Flussdichte:
-
Die elektrische Flussdichte kann als Feldgröße der
Ursache angesehen werden (verursachende Feldgröße),
bei der die Raumeigenschaft nicht in die Definition
eingeht
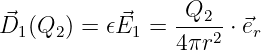 | (10.2.19) |
Entsprechend dem Raum-Richtungs-Einheitsvektor er, der immer auf
der Verbindunglinie zwischen Q1 (Wirkung) und Q2 (Ursache) liegt,
kann die Wirkung mehrerer Ladungen als vektorielle Überlagerung
betrachtet werden
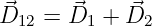 | (10.2.20) |
-
Einheit:
-
Die Einheit der (Verschiebungs-) Flussdichte ist
![[Q ] C A s
[D ] = --2-= --2 = --2
[r] m m](gde_352x.png) | (10.2.21) |
-
Interpretation:
-
An der Grenzfläche zwischen leitenden Plattenelektroden und dem
nicht leitenden Feldraum ist der Betrag der elektrischen Flussdichte im
Raum (Ladung pro Fläche) gleich dem Betrag der Ladungsdichte auf
den Platten (Ladung pro Fläche)
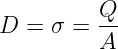 | (10.2.22) |
→ Bildhaft wird die Ladungsdichte σ an der Grenzfläche mit der
elektrischen Flussdichte D fortgeführt.
-
Materie:
-
Das elektrische Feld im Nichtleiter (anstelle von Vakuum) wird
ebenfalls mit der elektrischen Feldstärke und der Flussdichte
beschrieben, wenn anstelle von ϵ0 die Materialeigenschaften mit der
Dielektrizitätszahl ϵ über die relative Dielektrizitätszahl ϵr
berücksichtigt werden
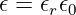 | (10.2.23) |
-
Spannung:
-
Durch Vorgabe einer Spannung U an einen Plattenkondensator
- findet eine Ladungstrennung auf den Platten statt.
-
Ladung:
-
Bei einem aufgeladenen Plattenkondensator, der von der
Spannungsquelle entfernt wurde
- entsteht eine Spannung zwischen den Platten.
Diese Ursache-Wirkungs-Prinzip am Beispiel des Plattenkondensators
ist in Tab. 10.1 dargestellt.
| | Kondensator mit
Spannungsquelle
verbunden | Kondensator von
Spannungsquelle
getrennt |
|
|
|
| Ursache | Spannung
U = const. | Ladung Q = const. |
| Formeln | E = U∕d | D = Q∕A |
| | D = ϵE | E = D∕ϵ |
| | Q = DA ∼ 1∕d | U = Ed ∼ d |
| Wirkung | Ladung Q = f(d) | Spannung U = f(d) |
|
|
|
| |
Tabelle 10.1: Ursache und Wirkung des elektrischen Feldes beim Kondensator
-
Genauer:
-
Schaut man sich den Urache-Wirkung-Zusammenhang etwas
mathematischer an, so findet man
Beiden Schaltungen liegt damit das selbe Gesezt Q = C ⋅U zugrunde.
Die „Konstante“ C werden wir später als Kapazität des Kondensators
bezeichnen.
-
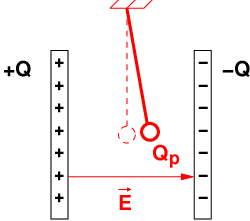
Influenz:
-
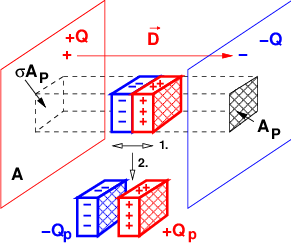
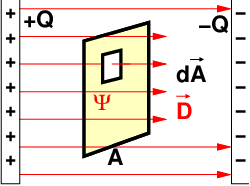
Trennt man zum Nachweis von D bzw. E in Abb. 10.2.9
die beiden Prüfplatten im elektrischen Feld und nimmt sie
dann heraus, so kann man auf jeder Platte die Ladung Qp
messen.
-
Ursache:
-
Die Ursache dieser influenzierten Ladungen ist die Feldstärke E, die
einen Teil der freien negativen Elektronen zur Oberfläche der einen
Platte verschiebt, so dass in der anderen Platte die ortsfesten positiven
Kernladungen überwiegen.
Abb. 10.2.9 zeigt zusätzlich noch die „Röhre“ mit dem Querschnitt der
Prüfplatten durch sich der elektrische Fluss des nächsten Kapitels
anschaulich darstellen lässt.
-
Definition:
-
Analog zur Berechnung der skalaren Größe Strom I = SA
aus der Stromdichte und der durchflossenen Fläche wird das
Produkt
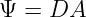 | (10.2.32) |
als elektrischer Fluss
(Fluss
= Flussdichte ⋅ Fläche) definiert.
Bei ebenen Flächen und konstantem Fluss gilt allgemeiner
entsprechend Abb. 10.2.10
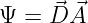 | (10.2.33) |
-
Inhomogen:
-
Bei beliebigen Flächen in inhomogenen Feldern muss der elektrische
Fluss als Summe über kleine Flächenelemente dA berechnet
werden
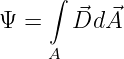 | (10.2.34) |
-
Gauß:
-
Was ergibt dieses Integral über eine geschlossene Fläche, einer
Hüllfläche? Der Gaußsche Satz
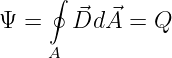 | (10.2.35) |
besagt, dass der elektrische Fluss durch eine geschlossene
Fläche gleich der von dieser Fläche eingeschlossenen Ladung
ist!
→ Wenn keine Ladungen eingeschlossen werden, muss das Hüllintegral Null
werden.
-
Maxwell:
-
Der Gaußsche Satz wird auch als 4. Maxwellsche Gleichung
bezeichnet. Er besagt, dass die Quellen und Senken des
elektrischen Feldes die positiven und negativen Ladungen
sind.
-
Influenz:
-
Betrachtet man den Verschiebungsfluss in Zusammenhang mit der
Ladungsverschiebung (Influenz in Leitern) in den Maxwellschen
Platten im elektrischen Feld des Kondensators, so kann man diesen
Verschiebungsfluss Ψ mit der zugehörigen Ladung Q auf den Platten
gleichsetzen
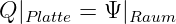 | (10.2.36) |
-
Strom:
-
Dann kann man aber auch einen Verschiebungsstrom iv im
Isolator definieren, der die Fortsetzung des Leitungsstromes ik
ist
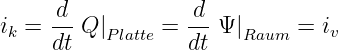 | (10.2.37) |
-
Frage:
-
Wieso hat das elektrische Feld eine Ladungsverschiebung auf den Platten
verursacht, obschon die leitenden Maxwellschen Platten elektrisch
isoliert
im Feldraum angebracht waren?
-
Polarisation:
-
Das elektrische Feld bewirkt eine Verschiebung der
Ladungsschwerpunkte positiver Atomkerne und negativer Elektronen
wodurch kleine elektrische Dipole entstehen. Dieser Vorgang heißt
dielektrische Polarisation der Nichtleiter.
→ Die Dipole vergrößern den Verschiebungsfluss. Der
Steigerungsfaktor wird durch die relative Dielektrizitätszahl
erfasst.
-
Dielektrika:
-
Dielektrika werden als Isolationswerkstoffe bei Kondensatoren (z.B.
Keramikkondensator
(Böhmer, 2004, Seite 46)) eingesetzt. In in Tab. 10.2 sind einige
Werkstoffe aufgeführt.
| Werkstoff | ϵr |
|
|
| SiO2 | 3,9 |
| Glas | 4…12 |
| Keramik NDK | < 500 |
| Keramik HDK | 500…10000 |
|
|
| |
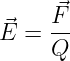
![1
[F-] N-- J-m-- -W-s-- -V-A V-
[E ] = [Q ] = A s = A s = m A s = m A = m](gde_325x.png)
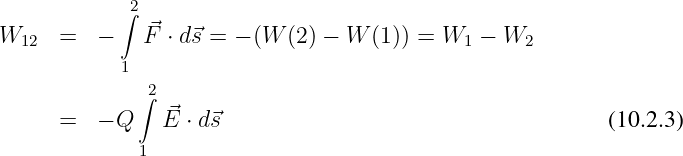
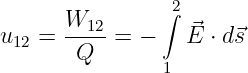
![[U ] = [W-] = W--s = V-A- = V
[Q ] A s A](gde_330x.png)
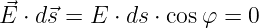
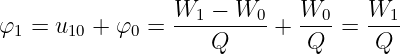
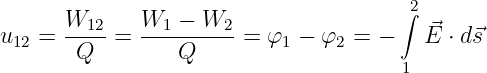
![[ ]
⃗E(x,y,z) = − grad φ = − ∂φ-, ∂-φ, ∂-φ
∂x ∂y ∂z](gde_336x.png)
![[ ]
⃗ ∂-- ∂-- ∂--
∇ = ∂x, ∂y, ∂z](gde_337x.png)
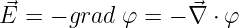
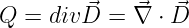
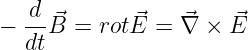
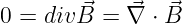
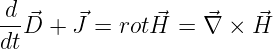
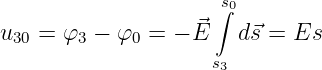
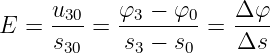
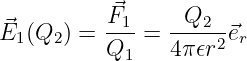
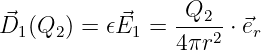
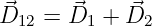
![[Q ] C A s
[D ] = --2-= --2 = --2
[r] m m](gde_352x.png)