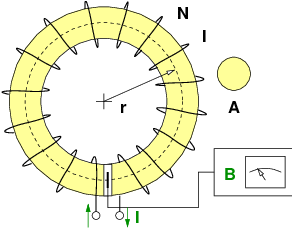
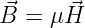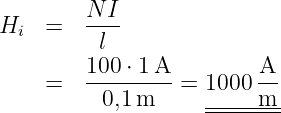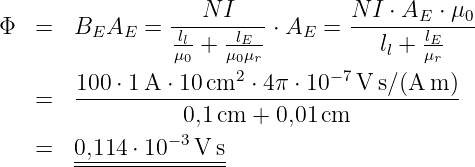Durchflutungsgesetz

12.3 Durchflutungsgesetz

Zusammenhang:

Das Durchflutungsgesetz beschreibt den Zusammenhang zwischen dem Strom und der von ihm erzeugten magnetischen Feldstärke wie in Abb. 12.3.1 dargestellt .¹⁵

Abbildung 12.3.1: Durchflutungsgesetz der magnetischen Feldstärke

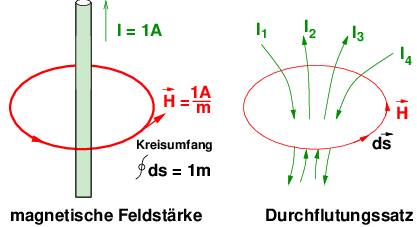
→ Bei einem geraden, unendlich langem Leiter durch den der Strom I = 1 A im Mittelpunkt eines Kreisring mit dem Umfang l = 1 m fließt ergibt sich entlang des Randes eine magnetische Feldstärke von H = 1 A∕m.

Durchflutung:

Für einen geschlossenen Umlauf entlang einer magnetischen Feldlinie ergibt der Durchflutungssatz¹⁶.

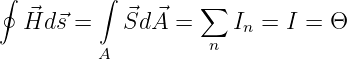∮ ∫ ∑ H⃗d ⃗s = ⃗SdA⃗ = In = I = Θ n A

(12.3.1)

Bedeutung:

Das Durchflutungsgesetz¹⁷ gilt unabhängig von der umgebenden Materie.

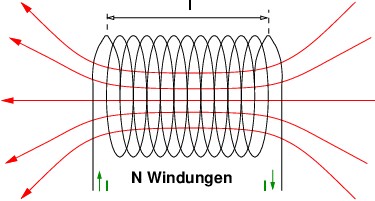
→ Es dient der Berechnung der magnetischen Feldstärke bei einfachen Leitergebilden, z.B. Zylinderspule.

→ Wird derselbe Strom I_x n-mal umfasst (z.B. in einer Spule), so wird er n-fach berücksichtigt I = nI_x.

Wirkung:

Elektrischer Strom ist von geschlossenen magnetischen Feldlinien (Wirbelfeld) umgeben.

→ Umkehrung: Geschlossene magnetische Feldlinien werden von einem Strom durchflossen (oder durchflutet, Durchflutungsgesetz).

Analogie:

Es besteht eine Analogie zum elektrischen Feld:

Der Ursache des elektrischen Feldes E entspricht der Vektor der magnetischen Feldstärke H.
Der Wirkungsgröße elektrische Flussdichte D im Nichtleiter und Stromdichte S im Leiter entspricht der Vektor der magnetischen Flussdichte B als Wirkung des Magnetfeldes.
Den Materialverknüpfungen ϵ $⃗D = ϵE⃗$
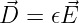
bzw. κ entspricht die Verknüpfung von B und H über die magnetischen Materialeigenschaften μ in jedem Raumpunkt
$B⃗ = μH⃗$

Beispiel 12.3.1 (Zylinderspule)

Bei einer Zylinderspule (siehe Abb. 12.3.2) kann davon ausgegangen werden, dass im Inneren der Spule durch Überlagerung der Einzelfelder¹⁸ eines jeden Leiters ein annähernd homogenes Feld H_i entsteht. Außerhalb der Spule ist das Feld H_a sehr schwach und kann dort vernachlässigt werden.

Abbildung 12.3.2: Beispiel zur magnetischen Feldstärke in einer Zylinderspule

Berechnen Sie für eine Zylinderspule in Luft der Länge l = 10 cm mit N = 100 Windungen den Betrag der magnetischen Feldstärke H_i für einen Strom I = 1 A.

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Magnetischen Feldstärke

H = N-I- i l 100 ⋅ 1 A A = --0,1m---= 1000 m- --------

Beispiel 12.3.2 (Kreisringspule)

Gegeben sei eine Kreisringspule (siehe Abb. 12.3.3) mit den Daten: Luftspaltlänge l_L = 1 mm, Eisenlänge l_E = 10 cm, relative Permeabilität in Eisen μ_r = 1000, Querschnittsfläche des Eisens A = 10 cm², Windungszahl N = 100.

Abbildung 12.3.3: Beispiel zum magnetischen Fluss in einer Kreisringspule

Berechnen Sie bei der dargestellten Kreisringspule den magnetischen Fluss Φ = BA für einen Strom I = 1 A.

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Magnetischer Fluss

N I N I ⋅ A ⋅ μ Φ = BEAE = -l----l-- ⋅ AE = -------El---0 μl0 + μ0Eμr ll + μEr 100 ⋅ 1A ⋅ 10cm2 ⋅ 4π ⋅ 10−7 V s∕(A m ) = ------------------------------------- 0,1cm + 0,01cm = 0,114-⋅ 10-−3V-s ---------------

¹⁵Genauer muss es heißen: … und der magnetischen Spannung V _m = ∫ Hds entsprechend Gln. 12.5.4, wobei diese Spannung aber erst später eingeführt wird.

¹⁶Bemerkung: Falls die Summe der Ströme Null ist ergibt sich auch kein magnetisches Feld. Anwendung: FI-Schutzschalter.

¹⁷auch Amperesches Gesetz und 1. Maxwellsche Gleichung genannt

¹⁸Superposition, analog zum E-Feld im Kondensator

[next] [prev] [prev-tail] [front] [up]