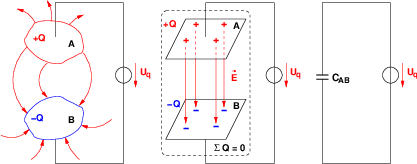
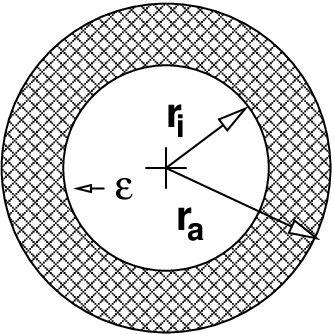
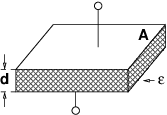
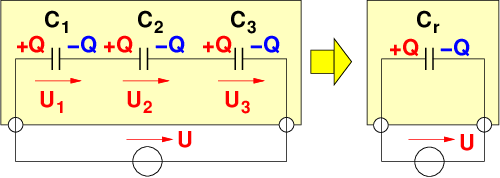
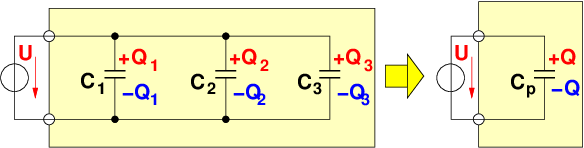
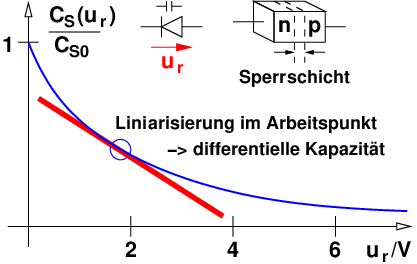
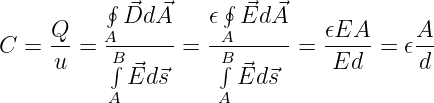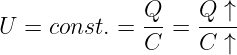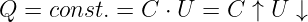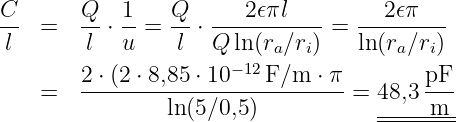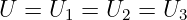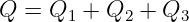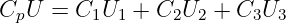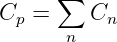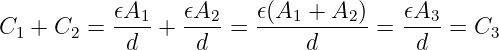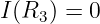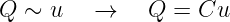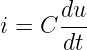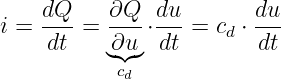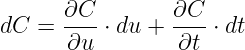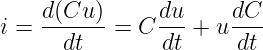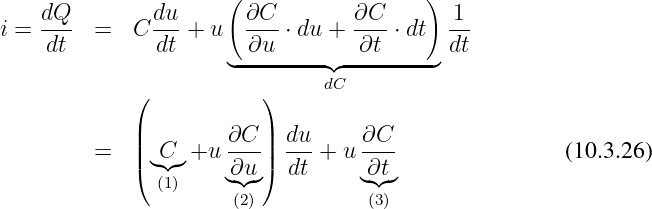Als Kondensator wird das Bauelement aus zwei leitenden Elektroden25 bezeichnet, die durch ein Dielektrikum26 getrennt sind. In Gleichstromkreisen bilden Kondensatoren eine Unterbrechung für den Strom. Warum, sollte man immer, nicht nur zur Prüfung wissen! Abb. 10.3.2 zeigt rechts zusätzlich das Schaltzeichen eines Kondensators. Die nicht miteinander verbundenen parallelen Striche verdeutlichen anschaulich, dass ein Gleichstrom im eingeschwungenen Zustand nicht über einen Kondensator fließen kann!
Das Verhältnis zwischen der Ladung auf den Kondensatorplatten und der Spannung zwischen ihnen wird als Kapazität definiert
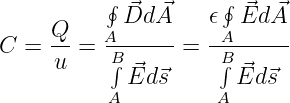 | (10.3.1) |
Die Einheit der Kapazität ist das Farad27
![[Q-] C- A-s -s
[C] = [U ] = V = V = Ω = F](gde_375x.png)
→ Ein Kondensator hat die Kapazität 1 F, wenn er bei einer Spannung 1 V die Ladung 1 C speichert. Die Einheit Farad ist für technische Kondensatoren zu groß — typische Kapazitäten liegen im Bereich von pF …mF (10-12 …10-3 F) wie in Tab. 10.3 aufgeführt.
| Kondensator | Kapazität |
| Speicherzelle eines 256 MBit-Speichers | 20 fF |
| Metallkugel mit r = 1 cm in Luft gegen eine ebene Elektrode im Abstand 1 m | 1 pF |
| Erde gegen Weltall | 700 µF |
| Fotoblitzkondensator | 1000 µF |
| Stabilisierungskondensator Autobatterie | 1 F |
Der Kondensator ist ein Energiespeicher. Er speichert Ladungen auf den Kondensatorplatten.
Noch offene Fragen sind:
- Wie gelangen Ladungen auf die Kondensatorplatten?
- Welcher Strom fließt?
- Wie verhält sich das Dielektrikum28 bei Stromfluss?
Da in einem Nichtleiter zwischen den Kondensatorplatten keine freien Ladungsträger sind, kann die Änderung der gespeicherten Ladung nur über die Zuleitungen als (Konvektions-) Strom erfolgen
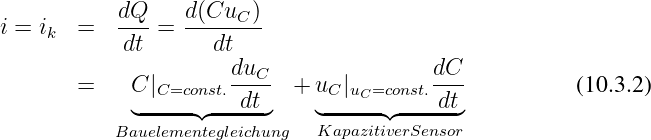
Für das Bauelement Kondensator, bei dem die Kapazität zeitlich konstant ist, vereinfacht sich Gln. 10.3.2 zur Bauelementegleichung des Kondensators29
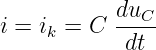 | (10.3.3) |
→ Ein Strom fließt über die Zuleitungen des Kondensators nur solange wie sich seine Klemmenspannung zeitlich ändert! Dementsprechend stellt ein Kondensator für Gleichspannung eine Unterbrechung dar.
Experimentell lässt sich nachweisen, dass während einer Ladungsänderung auch im Dielektrikum ein Magnetfeld existiert. Da umgekehrt ein Strom von einem Magnetfeld umgeben ist, lässt sich daraus schließen, dass durch das Dielektrikum ein „Strom fließt“, der nicht durch einen Ladungsträgertransport erzeugt wird. Er wird dielektrischer oder Verschiebungsstrom genannt30.
Fassen wir den Verschiebungsstrom iv im Nichtleiter als Fortsetzung des Konvektionsstromes in den Zuleitungen auf, so ergibt sich die Stromkontinuität zu
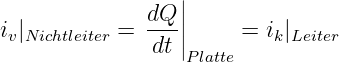 | (10.3.4) |
Ist der Strom gegeben mit dem sich die Ladung auf dem Kondensator ändert, so wird seine Spannung aus Gln. 10.3.3 mit
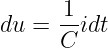 | (10.3.5) |
entsprechend nach der Integration von
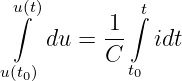 | (10.3.6) |
zu
![∫t
u (t) = u(t0) + 1- idt = u(t0) + 1-[Q(t) − Q(t0)]
C C
t0](gde_381x.png) | (10.3.7) |
Es lassen sich folgende Aussagen festhalten:
- Die Speicherwirkung des Kondensators zeigt sich darin, dass die Kondensatorspannung u von einer Anfangsspannung u(t0) abhängt, dem so genannten Anfangswert.
- Wird ein auf die Spannung u geladener Kondensator plötzlich kurzgeschlossen, so fließt anfangs ein sehr hoher Strom, da die Ladungsänderung gleich dem Zeitintegral des Stromes ist. Große Kondensatoren sollten daher nur kurzgeschlossen transportiert werden.
- Ein Spannungssprung am Kondensator ist nicht möglich, da sich die Ladung (und damit die Spannung) nur stetig ändern kann. Ein Stromstoß hingegen ist möglich und zudem u.U. sehr gefährlich!
Der Kondensator ist ein Energiespeicher. Wir wissen jetzt, wie die Ladung auf den Kondensator kommt.
→ Nächste Frage: Welche Energie hat er gespeichert, wenn er auf die Spannung U aufgeladen ist?
Während des Aufladens sind sowohl der Ladestrom als auch die Spannung am Kondensator eine Funktion der Zeit. In einer infinitesimal kleinen Zeit gilt für die Leistung die bekannte Beziehung p = ui. Der Kondensatorstrom kann durch Gln. 10.3.3 ersetzt werden und wir erhalten die aufgenommene Energie zu
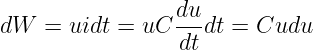 | (10.3.8) |
Die gespeicherte Energie nach Abschluss des Ladevorgangs erhalten wir durch Integration über die Kondensatorspannung von u = 0 bis u = U
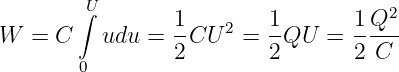 | (10.3.9) |