Das Induktionsgesetz

[next] [prev] [prev-tail] [tail] [up]

13.1 Das Induktionsgesetz

Wissen:

Eigentlich ergibt sich dieses Kapitel direkt aus der Theorie des stationären Magnetfeldes und dessen Anwendungen:

Nach dem Durchflutungsgesetz Gln. 12.3.1 ist ein stromdurchflossener Leiter von einem Magnetfeld umgeben.
Die Lorentzkraft nach Gln. 12.1.5 ist die Grundgleichung elektrischer Motoren.

Symmetrie:

In der Physik und damit auch in der Elektrotechnik sind die Gesetze oft symmetrisch:

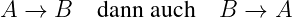
Wenn B aus A folgt, dann folgt auch A aus B: $A → B dann auch B → A$

Transfer:

Transferleistung durch Kombination¹:

Kann ein stationäres Magnetfeld einen Strom erzeugen?
Kann ein mechanisch angetriebener Motor einen Strom erzeugen?

Faraday:

Wer ist als erster auf die Idee gekommen, das der gefundene Zusammenhang auch umgekehrt funktionieren könnte?

→ Frage von Faraday: Kann ein Magnetfeld nicht auch einen Strom oder eine Spannung erzeugen?

Abbildung 13.1.1: Experiment zum Induktionsgesetz

Experiment:

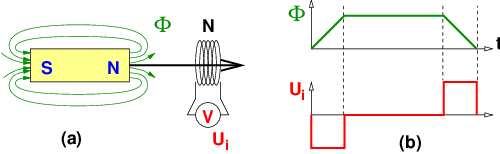
Wird ein Stabmagnet relativ zu einer Luftspule entsprechend Abb. 13.1.1 bewegt, so zeigt ein angeschlossenes Voltmeter eine Spannung solange der Magnet hinein bewegt wird. Wird der Magnet anschließend wieder heraus bewegt, erhält man eine entgegengesetzte Spannung.

Induktion:

Die magnetische Induktion B des Magneten erzeugt beim Einführen in die Spulenfläche A einen zeitlich veränderlichen magnetischen Fluss dΦ. Bei N Windungen der Spule wird die erzeugte Spannung

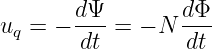u = − d-Ψ = − N dΦ- q dt dt

(13.1.1)

Gesetz:

Bezogen auf eine einzelne Windung erhalten wir mit dem Induktionsgesetz zu jeder zeitlichen Änderung des magnetischen Flusses durch eine von einem Leiter (oder gedachten Weg) umschlossenen Fläche die induzierte Spannung zu

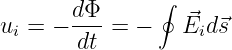d Φ ∮ ui = − --- = − ⃗Eid⃗s dt

(13.1.2)

→ Das Induktionsgesetz ist ein Naturgesetz, weil es zwei wesensfremde Größen² verknüpft. Nach dem Durchflutungsgesetz ist es die zweite grundlegende Gleichung der elektromagnetischen Feldbeschreibung³.

Fluss:

Die zeitliche Änderung des magnetischen Flusses Φ = B⋅A bedeutet bei homogenem magnetischen Feld

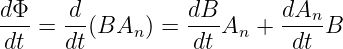dΦ d dB dAn --- = --(BAn ) = ---An + ----B dt dt dt dt

(13.1.3)

mit der Flächennormalen A_n von A in Richtung B.

Trafo:

Fließt durch eine feste Fläche A_n ein zeitveränderliches Magnetfeld B, so erhält man einen Transformator. Die sogenannte Ruheinduktion findet i.a. zur Transformation von Wechselspannungen Anwendung.

Generator:

Fließt durch eine zeitveränderliche Fläche A_n ein zeitlich konstantes Magnetfeld B, so erhält man einen Generator. Bei der sogenannten Bewegungsinduktion dreht sich i.a. eine Leiterschleife in einem Feld.

→ Umwandlung von mechanischer Arbeit in elektrischer Energie. Umkehrung des Gleichstrommotors!

¹Hier könnte man sich auch genereller Fragen: Wie kommt eigentlich DAS NEUE in die Welt?

²Spannung und magnetischer Fluss. Allgemeiner müsste es u_i = const.dΦ∕dt heißen, aber die Konstante ist 1

³der Maxwellschen Gleichungen

[next] [prev] [prev-tail] [front] [up]