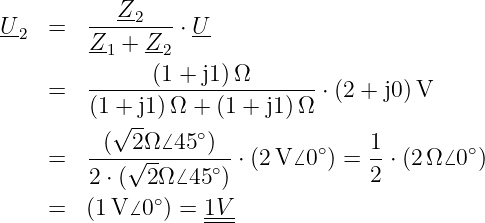[next] [prev] [prev-tail] [tail] [up]

Kapitel 5
Komplexe Rechnung

 5.1 Die komplexe Zahlenebene
 5.2 Rechenregeln für komplexe Zahlen
 5.3 Taschenrechner mit komplexer Rechnung
 5.4 Darstellung sinusförmiger Wechselgrößen
Ziele:

In diesem Kapitel werden die (hoffentlich bekannten) Grundlagen der komplexen Rechnung kurz und knapp wiederholt.

Die komplexe Rechnung ermöglicht eine effiziente Berechnung von Wechselstromschaltungen, wobei die zu lösenden Gleichungen denen der Gleichstromtechnik entsprechen.

→ So gibt es als Erweiterung des Spannungsteilers einen komplexen Spannungsteiler.

Anwendung:

Aufgrund der Leistungsfähigkeit selbst „kleiner“ Taschenrechner werden Aufgaben mit komplexen Zahlen in der Elektrotechnik heute wie Aufgaben mit reelen Zahlen direkt mit dem Taschenrechner durchgeführt — und zwar ohne explizite Umrechnung von Polarkoordinaten in Kartesische.

ZAHLEN:

Für die Gleichstromtechnik seien folgende Zahlenwerte gegeben: R1 = 1 Ω, R2 = 1 Ω und U = 2 V.

LÖSUNG:

Damit wird die Ausgangsspannung zu

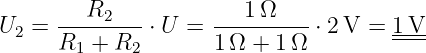
U2 = --R2----⋅ U = ---1-Ω--- ⋅ 2 V = 1V-- R1 + R2 1 Ω + 1 Ω ----

ZAHLEN:

Für die Wechseltromtechnik seien folgende Zahlenwerte gegeben: Z1 = (1 + j1) Ω, Z2 = (1 + j1) Ω und U = (2 + j0) V

LÖSUNG:

Damit wird die Ausgangsspannung zu

Z- U-2 = ----2---⋅ U Z1 + Z2 ------(1 +-j1)Ω------- = (1 + j1)Ω + (1 + j1) Ω ⋅ (2 + j0 )V √ -- ∘ -(-√2Ω⁄-45-)-- ⁄ ∘ 1- ⁄- ∘ = 2 ⋅ ( 2Ω ⁄ 45∘) ⋅ (2V 0 ) = 2 ⋅ (2 Ω 0 ) ⁄ ∘ = (1 V -0 ) = 1V-

[next] [prev] [prev-tail] [front] [up]