Die komplexe Zahlenebene

5.1 Die komplexe Zahlenebene

Imaginäre Zahl:

Senkrecht zur reellen Achse wird eine zweite Achse errichtet mit der imaginären Einheit

√ --- j = − 1

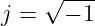(5.1.1)

wodurch sich die komplexe Zahlenebene ergibt.

Komplexe Zahl:

Eine komplexe Zahl besteht aus einem reellen Teil a und einem imaginären Teil jb (siehe Abb. 5.1.1)

r-= a + jb

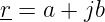(5.1.2)

Die komplexe Zahl r hat einen Wert a auf der reellen Achse und einen Wert b auf der imaginären Achse. Alternativ kann der Betrag r und der Winkel φ mit der reellen Achse zur Beschreibung verwendet werden.

Abbildung 5.1.1: Darstellung der komplexen Zahl

Konjugiert:

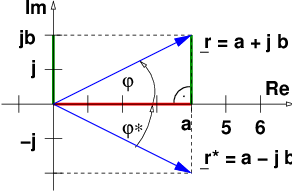
Zu der komplexen Zahl r läßt sich eine konjugiert komplexe Zahl definieren

r∗ = a − jb

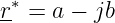(5.1.3)

Winkel:

Die Winkel φ und φ^∗ der komplexen Zahlen mit der reellen Achse (Nullphasenwinkel) sind

b φ = arctan a- − b φ∗ = arctan --- (5.1.4) a

Betrag:

Für den Betrag der komplexen Zahl oder die Länge des Zeigers gilt

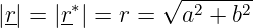√ ------- |r| = |r∗| = r = a2 + b2

(5.1.5)

Komponenten:

Für den Real- und Imaginärteil kann man damit auch schreiben¹

a = rcosφ b = rsinφ (5.1.6)

Alternativ:

Wir erhalten damit als gleichwertige Darstellungen

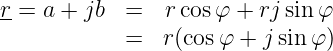r-= a + jb = r cosφ + rj sin φ = r(cosφ + j sin φ )

(5.1.7)

Euler:

Die Eulerschen Beziehungen zwischen den trigonometrischen Funktionen Sinus und Kosinus und der Exponentialfunktion sind

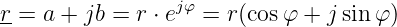jφ r-= a + jb = r ⋅ e = r(cosφ + j sin φ )

(5.1.8)

Da die e-Funktion hier nur als „Träger für den Winkel“ φ dient, kann man vereinfachend schreiben

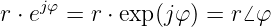r ⋅ ejφ = r ⋅ exp(jφ ) = r⁄ φ

(5.1.9)

Winkelfaktor:

Der Winkelfaktor e^jφ = φ zählt mathematisch positiv (entgegen dem Uhrzeigersinn). Beispiele für häufige Winkelfaktoren sind


φ = 0^∘ : exp	(j0) = cos	(0) + j sin	(0) =	1
φ = 90^∘ : exp	(jπ∕2) = cos	(π∕2) + j sin	(π∕2) =	j
φ = 180^∘: exp	(jπ) = cos	(π) + j sin	(π) =	−1
φ = 270^∘: exp	(j3π∕2)= cos	(3π∕2)+ j sin	(3π∕2)=	−j

φ = : exp

¹Dreiecksbeziehungen im rechtwinkligen Dreieck: sinφ = b∕r und cosφ = a∕r

[next] [prev] [prev-tail] [front] [up]