-
Gleichspannung:
-
Die Transformation einer Gleichspannung
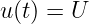 | (19.9.20) |
ergibt formal die Laplace-Transformierte
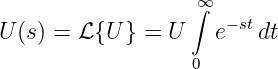 | (19.9.21) |
und mit der Integration
das Ergebnis
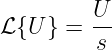 | (19.9.22) |
-
Sinus:
-
Die Transformation einer sinusförmigen Wechselspannung
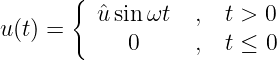 | (19.9.23) |
ergibt formal die Laplace-Transformierte
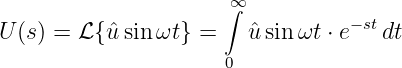 | (19.9.24) |
Mit dem Integral 322 (Weißgerber, 2000, Seite 462)
![∫ ax
eaxsin bx dx = --e---- ⋅ [a ⋅ sin bx − b ⋅ cos bx ]
a2 + b2](gde_4374x.png)
kann mit a = −s und b = ω die Integration durchgeführt werden
mit dem Ergebnis
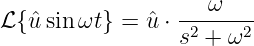 | (19.9.25) |
-
Kosinus:
-
Die Laplace-Transformierte einer kosinusförmigen Wechselspannung
ergibt analog
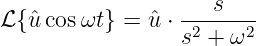 | (19.9.26) |
-
Phase:
-
Die Transformation einer sinusförmigen Wechselspannung mit
Anfangsphase
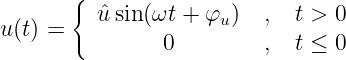 | (19.9.27) |
ergibt formal die Laplace-Transformierte
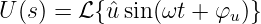 | (19.9.28) |
Mit der trigonometrischen Beziehung
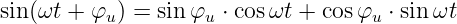
und dem Additionssatz wird daraus
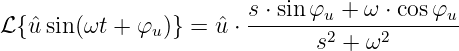 | (19.9.29) |
-
Schaltung:
-
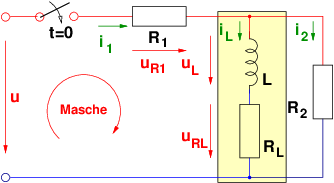
Als Beispiel wird die bereits bekannte Schaltung mit einer
Spule verwendet, bei der eine Wechselspannung entsprechend
Abb. 19.9.3 geschaltet wird.
Nach Gln. 19.5.9 war die DGL
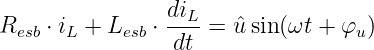
mit dem Ersatzwiderstand und der Ersatzinduktivität
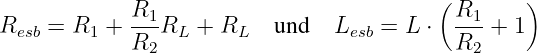
-
Spannung:
-
Die Laplace-Transformierte der Eingangsspannung ist mit
Gln. 19.9.29
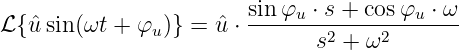
-
Gleichung:
-
![sinφu-⋅-s +-cos-φu-⋅ ω
ResbIL(s) + Lesb ⋅ [sIL(s) − iL(0)] = ˆu ⋅ s2 + ω2](gde_4386x.png) | (19.9.30) |
mit der Anfangsbedingung iL(0) = 0
-
Strom:
-
Die Laplace-Transformierte des Spulenstromes wird damit
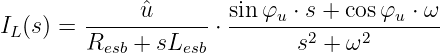 | (19.9.31) |
-
Zurück:
-
Mit der Rücktransformation 101 (Weißgerber, 2000, Seite
91)
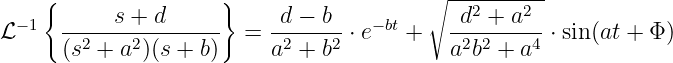
mit
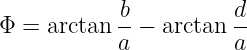
kann der Spulenstrom im Zeitbereich bestimmt werden
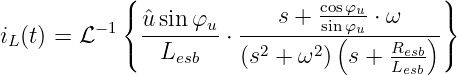 | (19.9.32) |
Der Vergleich mit der Korrespondenz ergibt
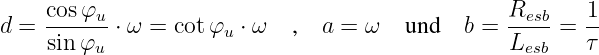
-
Ergebnis:
-
Wir erhalten direkt das Ergebnis zu
→ Hier sind wir eigentlich schon fertig! Der Beweis der Gleichheit
erfordert einige kleinere mathematische Umformungen, die zur
Vorbereitung einer mathematischen Klausur hilfreich sein können
…

![1-- 1-
[s] = [t] = s](gde_4349x.png)

![1 1 1
F (s ) = -f(0) + --ℒ{f ′(t)} = -[f(0) + ℒ {f′(t)}]
s s s](gde_4352x.png)
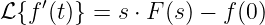
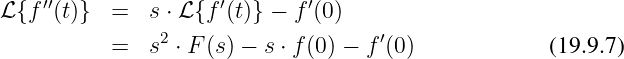
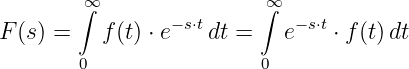
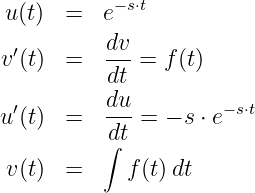
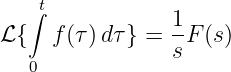
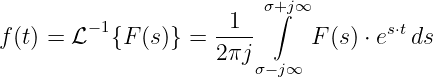
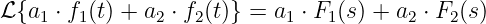
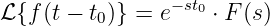
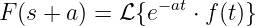
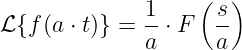
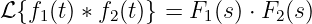
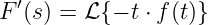
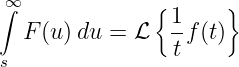
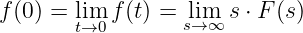
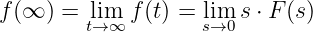
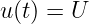
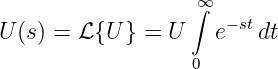
![U (s ) = U ⋅ 1--⋅ [e−st]∞
− s 0
U
= − --⋅ [0 − 1]
s](gde_4370x.png)
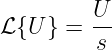
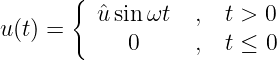
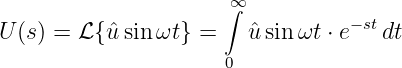
![∫ ax
eaxsin bx dx = --e---- ⋅ [a ⋅ sin bx − b ⋅ cos bx ]
a2 + b2](gde_4374x.png)
![U (s) = ---ˆu----⋅ [e−st ⋅ (− s ⋅ sin ωt − ω ⋅ cosωt )]∞0
s2 + ω2
---ˆu----
= s2 + ω2 ⋅ [0 − 1 ⋅ (− s ⋅ sin 0 − ω ⋅ cos0 )]](gde_4375x.png)
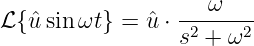
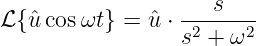
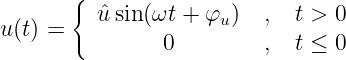
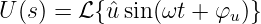
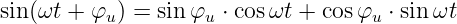
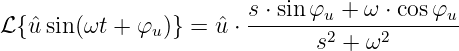
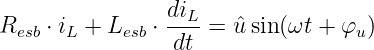
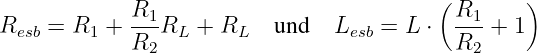
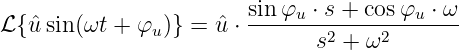
![sinφu-⋅-s +-cos-φu-⋅ ω
ResbIL(s) + Lesb ⋅ [sIL(s) − iL(0)] = ˆu ⋅ s2 + ω2](gde_4386x.png)
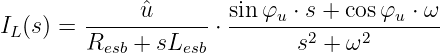
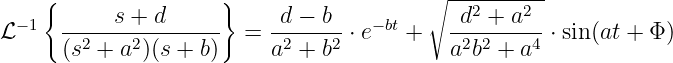
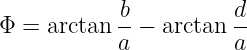
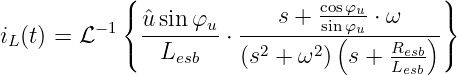
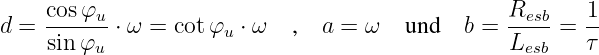
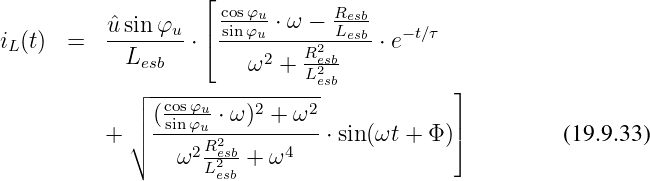
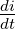
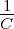
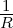
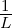
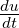
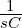
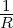
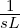
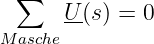
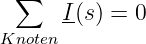
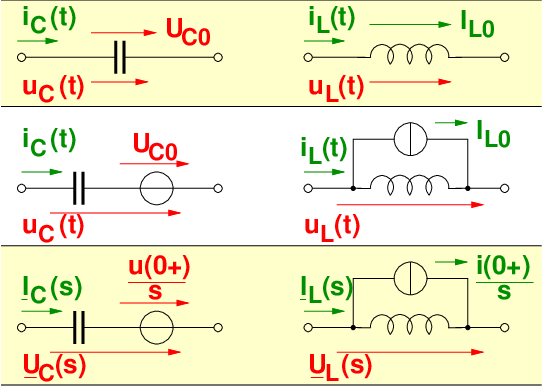
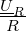
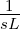
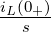
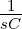
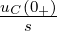

![{ 1 }
ℒ −1 ----------------- =
[ s(s − s1)(s − s2)]
--1--- ---1--- ( s1t s2t)
s1 ⋅ s2 ⋅ 1 + s1 − s2 ⋅ s2 ⋅ e − s1 ⋅ e](gde_4411x.png)
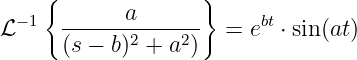
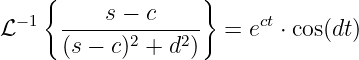
![uC (t) = 100V ⋅ [1 − 1,0008e −t∕8ms ⋅ sin(3,16ms −1 ⋅ t + 87,71∘)]
◟-----------◝◜-----------◞
------------------------------cos(3,16ms−1⋅t−2,29∘)-----](gde_4414x.png)