[next] [prev] [prev-tail] [tail] [up]

19.8 Fourier-Transformation

Ziel:

Mit Hilfe der Lapcace-Transformation wird eine Netzwerkberechnung mit einem Schaltvorgang aus dem Originalbereich (Zeitbereich) in den Bildbereich (Frequenzbereich) transformiert und dort gelöst. Anschließend wird das Ergebnis in den Originalbereich Rück-Transformiert.

Der Weg dahin ist:

  1. Die komplexe Fourierreihe wird auf Schaltvorgänge angewendet, bei denen sich das einmalige Schaltereignis mit einer Periode T → ∞ wiederholt (aperiodische Funktion).
  2. Durch den Übergang von der Summenbildung in der Fourierreihe zu Integralen entsteht die Fourier-Transformation.
  3. Um die schlechten Konvergenzeigenschaften der Fourier-Transformation zu beheben wird anstelle jω in der e-Funktion in der komplexen Fourierreihe die komplexe Frequenz s = σ + jω eingeführt, wodurch man zur Laplace-Transformation kommt.
Reihe:

Ausgangspunkt ist die komplexe Fourierreihe

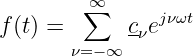∑∞ f(t) = cνejνωt ν=−∞
(19.8.1)

mit den komplexen Koeffizienten

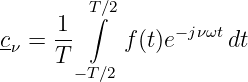1 T∫∕2 cν = -- f (t)e− jνωtdt T −T∕2
(19.8.2)

Spektrum:

Für den Übergang vom diskreten Spektrum mit ωT = 2π zum kontinuierlichen Spektrum wird aus der Grundfrequenz ω = Δω und damit

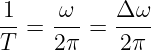1 ω Δ ω -- = --- = ---- T 2π 2π
(19.8.3)

Eingesetzt in die Koeffizientengleichung

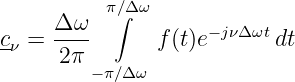Δ ω π∕∫Δ ω cν = ---- f (t)e−jνΔωt dt 2π −π∕Δω
(19.8.4)

Eingesetzt in die Fourierreihe

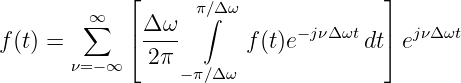⌊ ⌋ ∑∞ Δ ω π∕∫Δω f (t) = |⌈---- f(t)e−jνΔωtdt|⌉ ejνΔ ωt ν=− ∞ 2 π −π∕Δω
(19.8.5)

Durch den Grenzübergang Δω → 0 wird daraus

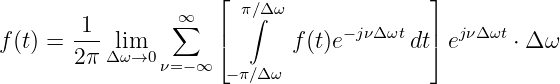∞ ⌊ π∫∕Δω ⌋ f(t) = 1-- lim ∑ | f(t)e− jνΔ ωtdt|ejνΔωt ⋅ Δ ω 2π Δω→0 ν=−∞ ⌈ ⌉ − π∕Δ ω
(19.8.6)

Mit Δω → 0 erhalten wir mit der kontinuierlichen Kreisfrequenz ω = νΔω

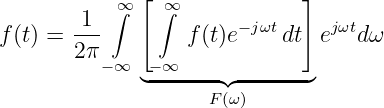∞∫ ⌊ ∫∞ ⌋ f(t) = -1- ⌈ f(t)e−jωtdt⌉ ejωtdω 2π −∞ − ∞ ◟-------◝◜------◞ F(ω)
(19.8.7)

Bedingung:

Dabei muss das uneigentliche Integral der Zeitfunktion

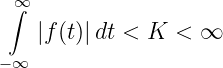
∞ ∫ |f(t)|dt < K < ∞ − ∞

absolut konvergent sein.

Transformation:

Damit erhalten wir die Gleichungen der Fourier-Transformation.

Mit der eigentlichen Fourier-Transformation

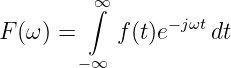∞ ∫ − jωt F (ω) = f (t)e dt −∞
(19.8.8)

erhalten wir zu einer Zeitfunktion f(t), deren Fourierintegral konvergiert,

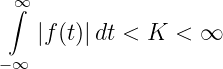∞ ∫ |f(t)|dt < K < ∞ −∞
(19.8.9)

das Spektrum F(jω).

Mit der sogenannten Rücktransformation

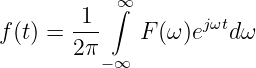∞∫ f(t) = -1- F(ω )ejωtdω 2π −∞
(19.8.10)

oder Inversen der Fourier-Transformation erhalten wir aus dem Spektrum F(jω) die zugehörige Zeitfunktion f(t) zurück

Problem:

In der Praxis gibt es schon bei einfachen Funktionen wie der Sprungfunktion, d.h. einer eingeschalteten Gleichspannung, Probleme mit der Konvergenzbedingung der Fouriertransformation aus Gln. 19.8.9.

Ansatz:

Die bisherige Zeitfunktion f(t) wird modifiziert gemäß

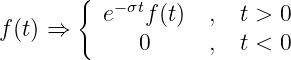{ −σt f(t) ⇒ e f(t) , t > 0 0 , t < 0
(19.8.11)

Es ergeben sich damit folgende Aussagen:

  1. Das Integral über das Produkt aus Sprungfunktion und Exponentialfunktion konvergiert für t > 0.
  2. Der problematische Bereich der Exponentialfunktion für t < 0 ist für technische Vorgänge uninteressant, da von der Vorgeschichte nur die Anfangswerte für t = 0 wichtig sind.
  3. Die Lösung wird also nur noch für den Zeitbereich t > 0 betrachtet.
Ergebnis:

Es ergibt sich eine neue Hintransformation

∞∫ [ ] F (ω ) = e−σtf(t) e− jωtdt 0∞ ∫ −(σ+jω)t = f (t)e dt (19.8.12) 0
und eine neue Rücktransformation für t > 0, wenn wir beide Seiten mit exp(σt) multiplizieren und diese von ω unabhängige Konstante unter das Integral ziehen
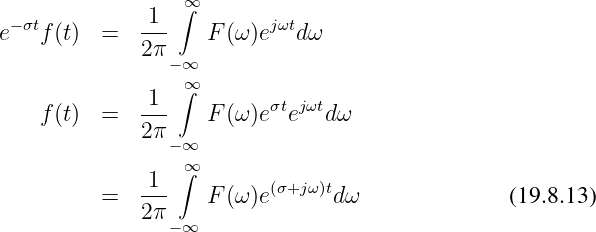
∞ −σt 1--∫ jωt e f(t) = 2π F (ω)e dω − ∞ ∫∞ f(t) = 1-- F (ω)eσtejωtdω 2π− ∞ ∫∞ 1-- (σ+jω)t = 2π F (ω)e dω (19.8.13) − ∞
Substitution:

Schreiben wir jetzt für die komplexe Frequenz

s = σ + jω
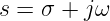(19.8.14)

so erhalten wir die Gleichungen der Laplace-Transformation.

[next] [prev] [prev-tail] [front] [up]