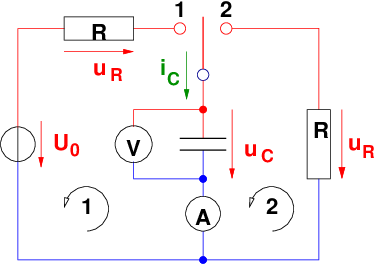
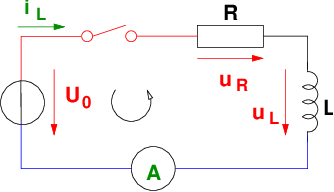
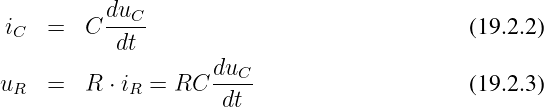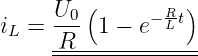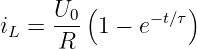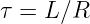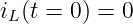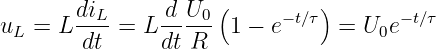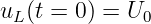Trennen der Variablen

19.2 Trennen der Variablen

Beispiel:

Für t = 0 wird der Schalter zum Kontakt 1 in Abb. 19.2.1 geschlossen.

Abbildung 19.2.1: Schaltung zur Kondensatoraufladung

Zeit:

Die Zustandsgröße u_C(t) wird von der Anfangsspannung³ u_C(t = 0) = 0V mit der Zeit ansteigen bis zum stationären Endwert u_C(t = ∞) = U₀, wenn der Strom durch den Widerstand Null geworden ist.

→ Ausgleichsvorgang, aber wie genau?

Masche:

Aufgrund der Maschenregel gilt

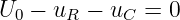U0 − uR − uC = 0

(19.2.1)

Hierin ist U₀ die zeitunabhängige Gleichspannung der Quelle und der Spannungsabfall am Widerstand u_R und am Kondensator u_C sind zeitabhängige Spannungen. Kleinbuchstaben kennzeichnen zeitabhängige Größen, d.h. u = u(t).

Bauelemente:

Mit den 2 bekannten Bauelementegleichungen

duC iC = C ---- (19.2.2) dt uR = R ⋅ iR = RC duC- (19.2.3) dt

wobei sich aus einer Knotengleichung i_R = i_C ergibt.

Masche:

In die Maschengleichung eingesetzt erhalten wir damit

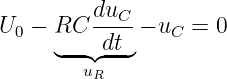duC- U0 − RC dt − uC = 0 ◟-u◝◜--◞ R

(19.2.4)

DGL:

Das ergibt eine Differentialgleichung zur Bestimmung der Kondensatorspannung

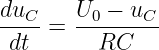duC-= U0-−-uC- dt RC

(19.2.5)

Lösung:

Gesucht ist u_C, das diese DGL erfüllt. Die Lösung erhält man mit der Substitution

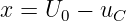x = U − u 0 C

(19.2.6)

und deren Ableitung

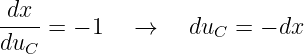dx ---- = − 1 → duC = − dx duC

(19.2.7)

über

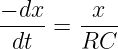−-dx-= --x- dt RC

(19.2.8)

und Trennen der Veränderlichen aus

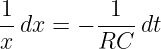1- -1-- x dx = − RC dt

(19.2.9)

Mit einer unbestimmten Integration folgt

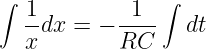∫ 1- -1--∫ x dx = − RC dt

(19.2.10)

Das Ergebnis der Integration ist

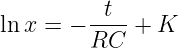t lnx = − ----+ K RC

(19.2.11)

Ersetzen der Konstanten durch K = ln k liefert weiter

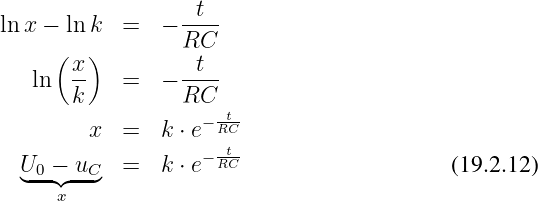
t ln x − lnk = − RC-- ( x) t ln -- = − ---- k RC x = k ⋅ e− tRC − tRC- U◟0-−◝◜uC◞ = k ⋅ e (19.2.12) x

Aus der Anfangsbedingung von u_C(t = 0) folgt

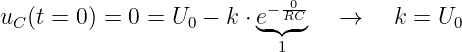u (t = 0) = 0 = U − k ⋅ e−R0C → k = U C 0 ◟ ◝◜-◞ 0 1

(19.2.13)

Spannung:

Damit erhalten wir die gesuchte Lösung zu

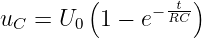( −RtC-) uC = U0 1 − e

(19.2.14)

mit der Zeitkonstanten

τ = RC

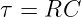(19.2.15)

Strom:

Mit Gln. 19.2.2 erhalten wir den Strom zu

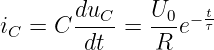duC U0 t iC = C ---- = ---e− τ dt R

(19.2.16)

Zeitkonstante:

Die Kondensatorspannung nach Gln. 19.2.14 würde aus jedem Zeitpunkt t = t_x mit konstant gehaltener Steigung

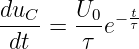duC-= U0-e− tτ dt τ

(19.2.17)

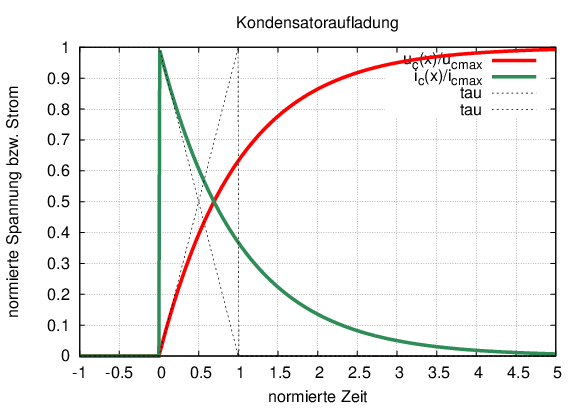
den Endwert U₀ nach Ablauf der Zeit t = τ erreichen. Für t_x = 0 ist dieses in Abb. 19.2.2 mit eingezeichnet.

Kennlinie:

Die Kondensatorspannung in Abb. 19.2.2 steigt nach einer Exponentialfunktion an und wird erst nach langer Zeit gleich der Spannung der Quelle. Der für den Anfangszeitpunkt maximale Strom nimmt mit der Zeit exponentiell gegen Null ab.

→ Normierte Funktionen: u_C(x)∕u_cmax = 1 − exp(−x) und i_C(x)∕i_cmax = exp(−x) mit x = t∕τ.

Abbildung 19.2.2: Spannung und Strom bei der Kondensatoraufladung

Entladung:

Nachdem der Kondensator aufgeladen ist, wird der Schalter in Abb. 19.2.1 in Stellung 2 gebracht. Aufgrund der Maschenregel gilt jetzt

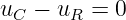uC − uR = 0

(19.2.18)

und mit dem Kondensatorstrom, der entgegengesetzt zum Strom durch den Widerstand (u_R = Ri_R = −Ri_C) ist, erhalten wir

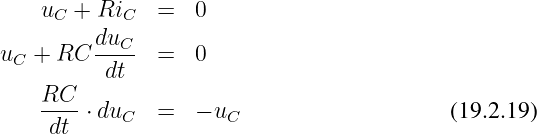
uC + RiC = 0 duC- uC + RC dt = 0 RC ----⋅ duC = − uC (19.2.19) dt

DGL:

Entsprechend der Kondensatoraufladung ergibt sich die Ausgangsdifferentialgleichung durch Trennen der Variablen direkt zu

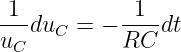1 1 ---duC = − ----dt uC RC

(19.2.20)

Lösung:

Entsprechend der Kondensatoraufladung ergibt sich als Lösung der unbestimmten Integration

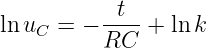t ln uC = − ----+ lnk RC

(19.2.21)

Spannung:

Mit der Anfangsbedingung u_C(t = 0) = U₀ wird die Kondensatorspannung zu

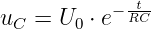-t- uC = U0 ⋅ e−RC

(19.2.22)

Strom:

Mit Gln. 19.2.2 erhalten wir den Strom zu

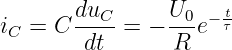duC U0 − t iC = C -dt- = − -R-e τ

(19.2.23)

→ Auch hier springt der Kondensatorstrom im Schaltzeitpunkt von dem Wert i_C(t₋₀) = 0A auf den Wert i_C(t₊₀) = −U₀∕R.

Kennlinie:

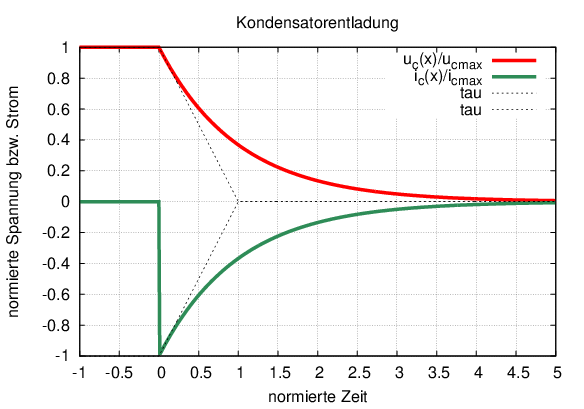
Die Kondensatorspannung in Abb. 19.2.3 fällt von einem Anfangswert U₀ exponentiell auf Null ab. Bei Ladung und Entladung bleibt die Spannung dauernd im positiven Bereich, aber die Stromrichtung ändert sich.

→ Normierte Funktionen: u_C(x)∕u_cmax = exp(−x) und i_C(x)∕i_cmax = −exp(−x) mit x = t∕τ.

Abbildung 19.2.3: Spannung und Strom bei der Kondensatorentladung

Beispiel 19.2.1 (Spule)

Eine Spannungsquelle wird über einen Schalter an eine reale Spule angeschlossen. Auf den Innenwiderstand der Spannungsquelle kann ja verzichtet werden, da in den Gleichungen immer nur die Summe des Innenwiderstandes und des Kupferwiderstandes vorkommt.

Abbildung 19.2.4: Schaltung zur Messung des Stromanstiegs in einer Spule

Kann man auch eine ideale Spule an eine ideale Spannungsquelle anschließen?
Was passiert, wenn man den geschlossenen Schalter bei einer realen Spule wieder öffnet?
Es ist der zeitliche Verlauf des Spulenstroms mit Hilfe des Verfahrens Trennen der Variablen zu berechnen!

LÖSUNG:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

U0-( − RLt) iL = R---1-−-e-----

Ergebnis:

Für den Stromanstieg erhalten wir eine formal ähnliche Beziehung wie für den Spannungsanstieg beim Kondensator

U0 ( ) iL = --- 1 − e−t∕τ R

(19.2.24)

mit der Zeitkonstanten

τ = L ∕R

(19.2.25)

Spannung:

Der Anfangswert des Stromes ist
$iL(t = 0) = 0$ (19.2.26)
Die Spulenspannung ist
$diL- d-U0-( − t∕τ) −t∕τ uL = L dt = L dt R 1 − e = U0e$ (19.2.27)

Der Anfangswert der Spulenspannung ist

uL(t = 0) = U0

(19.2.28)

→ Die Spulenspannung springt im Schaltzeitpunkt von dem Wert u_L(t₋₀) = 0V auf den Wert u_L(t₊₀) = U₀.

³Dieser Anfangszustand hängst natürlich immer von der tatsächlichen Schaltung ab! In dieser Aufgabe sei der Kondensator vollständig entladen gewesen.

[next] [prev] [prev-tail] [front] [up]