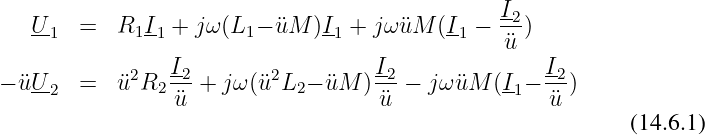Alle Vierpole, deren Klemmenverhalten durch die Transformatorgleichungen 14.2.5 beschrieben wird, verhalten sich nach außen (d.h. an den Klemmen 1, 1’, 2 und 2’ in Abb. 14.6.1 ) wie ein Transformator und können somit als Transformator-Ersatzschaltung verwendet werden.
In Gln. 14.2.5 subtrahiert man in der ersten Gleichung vom zweiten Summanden den Wert jωüMI1 und addiert ihn zum dritten hinzu. In der zweiten Gleichung verfährt man analog, nachdem diese zuvor mit ü multipliziert wurde mit dem Term jωMI2.
Man erhält dann für Masche 1 und 22
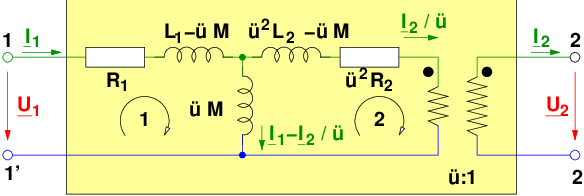
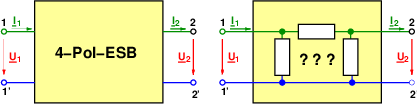
Die Gleichungen 14.6.1 beschreiben die Transformatorersatzschaltung entsprechend Abb. 14.6.2.
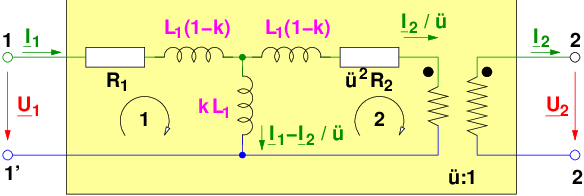
Ist Abb. 14.6.3 das auch ein richtiges ESB des Transformators?
Wie können Sie überprüfen, ob die Transformatorgleichungen 14.2.5 diese Schaltung beschreiben?
So geht es:
- Was bedeutet die Variable k?
- Auftstellen der Maschengleichungen!
- Umformen der Maschengleichungen!
Das Übersetzungsverhältnis ist gegeben durch Gln. 14.4.6 zu
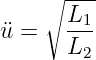 | (14.6.2) |
Zur besseren Übersicht wird der Kopplungsfaktor eingeführt
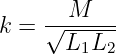 | (14.6.3) |
Da nur in Idealfall totaler Kopplung (d.h. streuungsfrei) M = 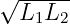 wird, gilt beim realen Transformator 0 < k < 1.
wird, gilt beim realen Transformator 0 < k < 1.
Erweitert man Gln. 14.6.3 mit 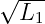 ∕
∕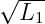 so erhält man mit
Gln. 14.6.2
so erhält man mit
Gln. 14.6.2
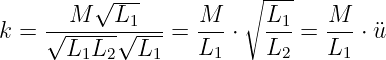 | (14.6.4) |
die Beziehung für die Hauptinduktivität
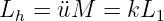 | (14.6.5) |
Stellen wir nun die Maschengleichungen für das ESB in Abb. 14.6.3 auf. Für die linke Masche erhalten wir:
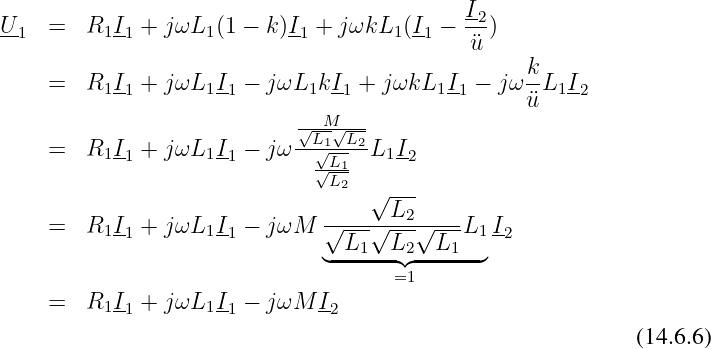
Und für die rechte Masche entsprechend:
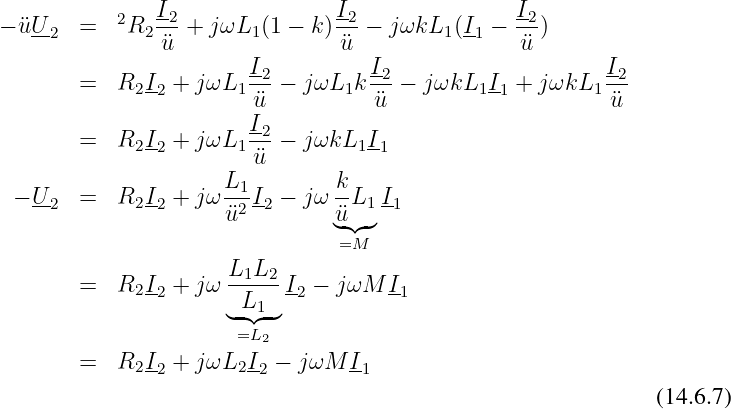
Zur Beschreibung der Streuung beim realen Transformator wird zusätzlich der Streufaktor definiert
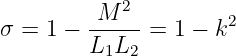 | (14.6.8) |
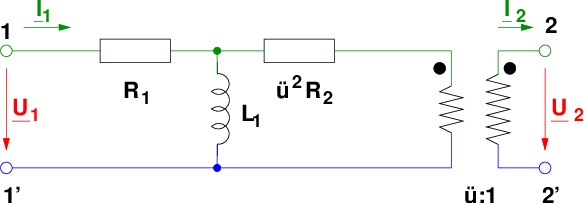
Im Grenzfall idealer Kopplung (k = 1) erhalten wir das Ersatzschaltbild eines streuungsfreien Transformators mit Verlusten (siehe Abb. 14.6.4 .