Der verlustlose und streuungsfreie Transformator

14.4 Der verlustlose und streuungsfreie Transformator

Streuungsfrei:

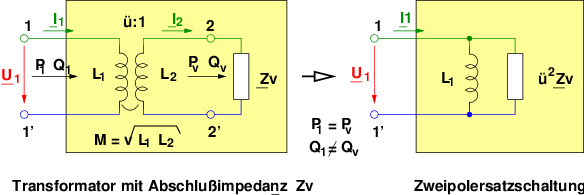
Bei streuungsfrei gekoppelten Wicklungen ist der gesamte Fluss ϕ₁ der Wicklung 1 mit der ganzen Wicklung 2 verkettet (siehe Abb. 14.2.2) und es gilt dann

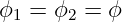ϕ1 = ϕ2 = ϕ

(14.4.1)

Mit N₁ϕ₁ und N₂ϕ₂ aus Gln. 14.2.3 ergibt sich

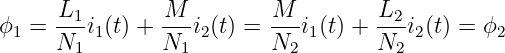L M M L ϕ1 = -1-i1(t) + ---i2(t) = ---i1(t) + --2i2(t) = ϕ2 N1 N1 N2 N2

(14.4.2)

Vergleich:

Schreiben wir dafür einmal mathematisch einfacher

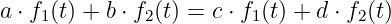
a ⋅ f1(t) + b ⋅ f2(t) = c ⋅ f1(t) + d ⋅ f2(t)

können wir relativ einfach eine Aussage zu den Koeffizienten der Zeitfunktionen machen, wenn wir z.B. f₁(t) oder f₂(t) zu Nullsetzen. Dann müssen die Koeffizienten auf beiden Gleichungsseiten der selben Zeitfunktion identisch sein zu jedem Zeitpunkt

a = c b = d (14.4.3)

Ergebnis:

Für die Koeffizienten der beiden Zeitfunktionen i₁(t) und i₂(t) bedeutet das dann

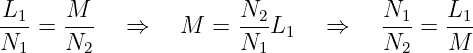L1- M-- N2- N1- L1- N = N ⇒ M = N L1 ⇒ N = M 1 2 1 2

(14.4.4)

und

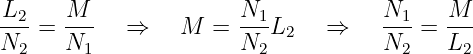L M N N M -2-= --- ⇒ M = -1-L2 ⇒ --1 = --- N2 N1 N2 N2 L2

(14.4.5)

Ergebnis:

Gleichsetzen von M liefert für den streuungsfreien Transformator mit dem Windungszahlverhältnis ü

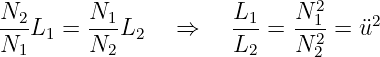2 N2- N1- L1- N-1 2 N1 L1 = N2 L2 ⇒ L2 = N 22 = ¨u

(14.4.6)

und analog Gleichsetzten von N₁∕N₂

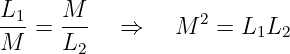L1 M 2 ---= --- ⇒ M = L1L2 M L2

(14.4.7)

Strom:

Setzt man diese beiden Ergebnisse in Gln. 14.3.5 ein, so ergibt sich

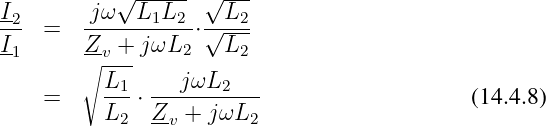
I- jω√L--L-- √L--- -2- = -------1-2-⋅√---2 I1 Z∘v-+-jωL2 L2 L1 jωL2 = ---⋅----------- (14.4.8) L2 Zv + jωL2

Das Stromverhältnis beim verlust- und streuungsfreien Transformator wird dann

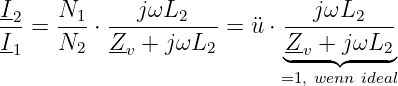I2= N1- ⋅---jωL2----= u¨⋅ --j-ωL2---- I1 N2 Zv + jωL2 Zv + jωL2 ◟---◝◜---◞ =1, wenn ideal

(14.4.9)

Bemerkung:

Wenn der Term beim idealen Tranformator zu 1 werden soll ist das bei vorgegebener Frequenz ω und Lastimpedanz Z_v nur möglich für L₂ →∞. Das werden wir aber erst später verwenden.

Spannung:

Setzt man Gln. 14.4.7 in Gln. 14.3.8 ein, so ergibt sich für Z_v≠0

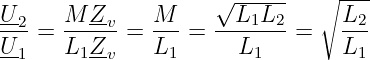√ ----- ∘ --- U-2= M-Zv--= -M- = --L1L2- = L2- U-1 L1Zv L1 L1 L1

(14.4.10)

Das Verhältnis der Sekundär- zur Primärspannung beim verlust- und streuungsfreien Transformator ist damit

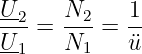U2 N2 1 ---= ---= -- U1 N1 ¨u

(14.4.11)

Eingang:

Setzt man den Strom I₂ aus Gln. 14.3.4 in Gln. 14.3.1 der Spannung U₁ ein

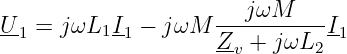U = jωL I − jωM ---jωM-----I -1 1-1 Zv + jωL2 -1

(14.4.12)

so erhält man den Eingangswiderstand

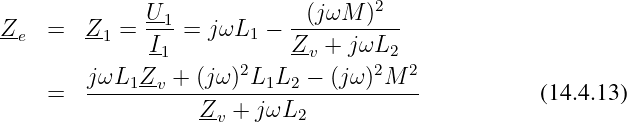
U- (jωM )2 Ze = Z1 = --1 = jωL1 − ----------- I1 Zv + j ωL2 jωL1Zv--+-(jω)2L1L2-−--(jω)2M-2- = Z + jωL (14.4.13) -v 2

Aus Gln. 14.4.7 setzen wir M² = L₁L₂ ein und erhalten

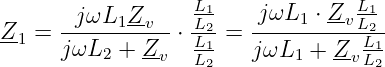jωL Z L1 jωL ⋅ Z L1 Z1 = -----1-v---⋅LL2-= -----1---vL2L- jωL2 + Zv L12 jωL1 + Zv L12

(14.4.14)

Ergebnis:

Mit L₁∕L₂ = ü² (Gln. 14.4.6) wird die Eingangsadmittanz Y ₁ des verlust- und streuungsfreien Transformators

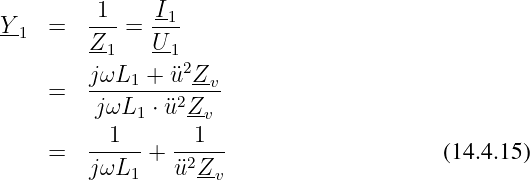
-1- I1- Y1 = Z = U -1 --12 = jωL1-+--¨u-Zv- jωL1 ⋅ ¨u2Zv 1 1 = ----- + -2--- (14.4.15) jωL1 ¨u Zv

An den Primärklemmen sieht man eine Admittanz, die aus der Parallelschaltung zweier Teiladmittanzen besteht.

Last:

Die Eingangsadmittanz Y ₁ enthält nicht einfach den Summanden 1∕Z_v, sondern die Lastimpedanz Z_v wird mit ü transformiert zu 1∕ü²Z_v

Abbildung 14.4.1: Impedanzwandlung im verlust- und streuungsfreien Transformator

Praxis:

Diesen Anpassungsübertrager, siehe Abb. 14.4.1 kann man zur Leistungsanpassung wie im Beispiel 14.5.1 einsetzen.

[next] [prev] [prev-tail] [front] [up]