[next] [prev] [prev-tail] [tail] [up]

14.5 Der ideale Transformator

Ideal:

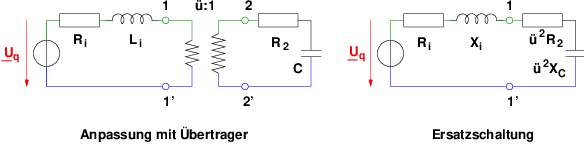
Ein Transformator, bei dem die Induktivitäten L1 = L2 = ∞ werden und damit auch die Gegeninduktivität M = ∞ wird, nennt man einen Übertrager.

→ Es kann in Abb. 14.4.1 dann der induktive Widerstand jωL1 weggelassen werden.

Spannung:

Für die Spannungsübersetzung des Übertragers gilt weiterhin

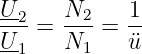U2-= N2-= 1- U1 N1 ¨u
(14.5.1)

Strom:

Die Stromübersetzung des Übertragers erhalten wir bei endlichen Zv zu

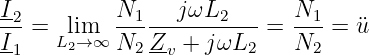I N jωL N -2-= lim --1-------2---= --1= ¨u I1 L2→ ∞ N2 Zv + j ωL2 N2
(14.5.2)

Eingang:

Die Eingangsimpedanz reduziert sich auf

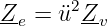Ze = ¨u2Zv
(14.5.3)

Impedanz:

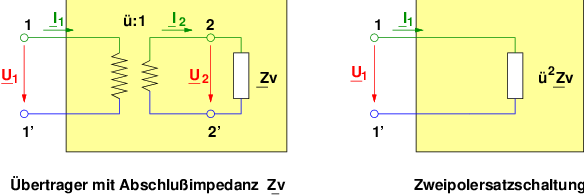
Der Übertrager transformiert die Ausgangsimpedanz mit ü2 auf die Primärseite (siehe Abb. 14.5.1 mit Schaltsymbol) .

PIC

Abbildung 14.5.1: Impedanzwandlung mit Übertrager

→ Der Übertrager ist ein Vierpol, der selbst weder Blind- noch Wirkleistung aufnimmt.

Beispiel 14.5.1
(Anpassung)

Eine Spannungsquelle hat eine innere Impedanz Zi = Ri+jωLi. Ein Verbraucher mit dem ohm’schen Widerstand R2 = 400Ri soll eine möglichst große Leistung aufnehmen.

PIC

  1. Welchen Wert muss das Übersetzungsverhältnis ü = N1∕N2 des idealen Übertragers haben?
  2. Wie groß muss der Kondensator als Funktion von Li gewählt werden?
  3. Wie groß ist der Kondensator bei f = 50 Hz für Li = 1 mH?

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

  1. Übersetzungsverhältnis
    ∘ ---- R 1 ¨u = --i = --- R2 20-

  2. Kondensatorwert
    ¨u2 C = --2-- ω--Li- 1 = 202-⋅ (2-⋅ π-⋅ 50Hz-)2 ⋅-1mH = 25,3-µF

[next] [prev] [prev-tail] [front] [up]