[next] [prev] [prev-tail] [tail] [up]

14.2 Transformatorgleichung

Ziel:

Das Ersatzschaltbild des realen Transformators ist identisch mit dem ESB der Asynchronmaschine. Das beim Transformator hergeleitete ESB kann dann später bei der ASM verwendet werden.

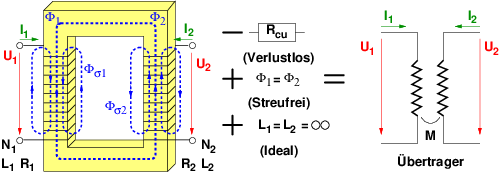
Abb. 14.2.1 stellt den Weg von realen Transformator mit Verlusten und Streuung hin zum Übertrager dar, einem idealen Transformator. Im Einzelnen bedeutet das:

PIC

Abbildung 14.2.1: Transformator: Aufbau und Übersicht
Verluste:

Beim verlustlosen Transformator werden die Kupferverluste in den Wicklungswiderständen zu R1 = R2 = 0.

Streuung:

Bei einem streufreien Transformator mit ϕ1 = ϕ2 gehen die magnetischen Flüsse vollständig durch die beiden Wicklungen.

Ideal:

Den idealen Transformator erhalten wir mit idealen Induktivitäten L1 = L2 = ∞.

Übertrager:

Der ideale Transformator transformiert Spannungen und Ströme gemäß

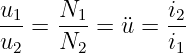u1 N1 i2 ---= --- = ¨u = -- u2 N2 i1

Kopplung:

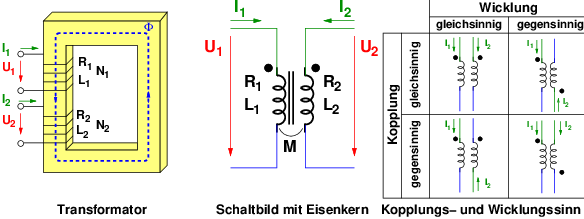
Wenn bei beiden Spulen in Abb. 14.2.2 der Strom, der in die Klemme mit dem Punkt eintritt, positiv ist, so haben deren Beiträge zum Hauptfluss die gleiche Richtung. Der Transformator in Abb. 14.2.3 ist also gleichsinnig gewickelt und gegensinnig gekoppelt. Die Stromrichtungen entsprechen dort dem Verbraucherzählpfeilsystem.

PIC

Abbildung 14.2.2: Transformator mit Schaltbild, Wicklungs- und Kopplungssinn
Spulen:

Werden anstelle einzelner Leiterschleifen Spulen mit den Windungen N1 und N2 verwendet, so wird aus Gln.  14.1.1

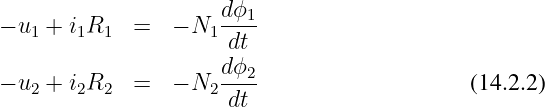
dϕ1 − u1 + i1R1 = − N1 ---- dt − u2 + i2R2 = − N2 dϕ2- (14.2.2) dt
Teilflüsse:

Für die magnetischen Flüsse gilt

N1ϕ1 = L1i1 + M i2 N2ϕ2 = L2i2 + M i1 (14.2.3)
Transformatorgleichungen:

Wir erhalten dann identisch zu Gln. 14.1.9 wieder

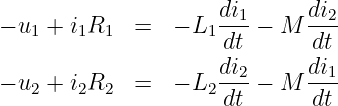
di1 di2 − u1 + i1R1 = − L1 dt − M dt di di − u2 + i2R2 = − L2--2 − M --1 dt dt
Verbraucher:

Wird an der Sekundärklemme ein Verbraucher angenommen, so wird dort zweckmäßiger Weise auch das Verbraucherzählpfeilsystem (VZS) verwendet, bei dem der Strom i2 eine umgekehrte Richtung erhält. Die Transformatorgleichungen werden dann zu

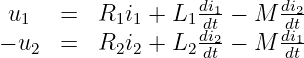u1 = R1i1 + L1 ddi1t-− M ddi2t- − u2 = R2i2 + L2 ddi2t-− M ddi1t-

Komplex:

Im eingeschwungenen Zustand erhalten wir für die komplexen Effektivwerte (Ansatz: I = I exp jωt)

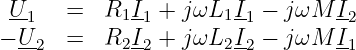U-1 = R1I1-+ jωL1I1-− jωM I2 − U-2 = R2I2-+ jωL2I2-− jωM I1

Frage:

Ist der ideale Übertrager in diesem Gleichungssystem enthalten, oder wie kann dieses Gleichungssystem zur einfachen Gleichung des idealen Übertragers überführt werden?

Kopplung:

Im VZS ist bei gleichsinner Wicklung (Punkte oben in Abb. 14.2.3 ) eine gegensinnige Kopplung vorhanden, d.h. die magnetischen Teilflüsse als Folge von I1 und I2 wirken entgegengesetzt, wie in Gln. 14.2.5 zu sehen ist.

PIC


Abbildung 14.2.3: Transformator mit unsymmetrischen Stromzählpfeilen im VZS

Bei gleichsinniger Kopplung bleiben die Gleichungen 14.2.5 bestehen, aber M wirkt verstärkend:

→ Die Ausdrücke mit M werden positiv.

Ziel:

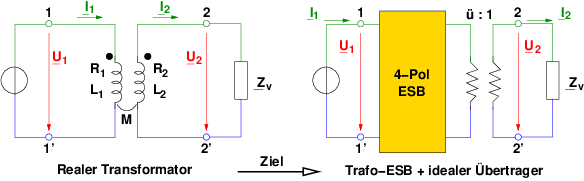
Gesucht wird eine Ersatzschaltung des realen Transformators mit:

Fertig:

Wann stimmt das Trafo-ESB mit dem Original überein?

→ Triviale Lösung: Wenn sich aus den beiden Maschengleichungen im Trafo-ESB die Transformatorgleichungen herleiten lassen!

Damit erhalten wir dann auch:

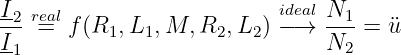I2 real idealN1 --- = f(R1, L1,M, R2, L2) −→ --- = u¨ I1 N2

und

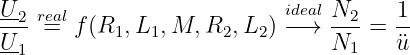U-2real ideal N2- 1- U- = f(R1, L1,M, R2, L2) −→ N1 = ¨u 1

[next] [prev] [prev-tail] [front] [up]