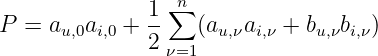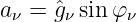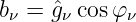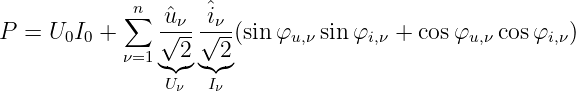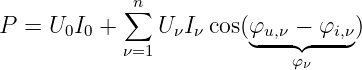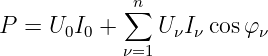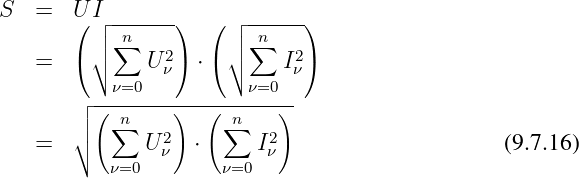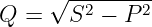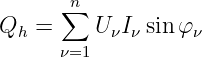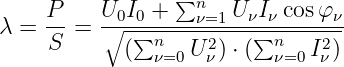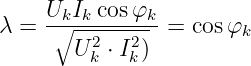-
Wirkleistung:
-
Die Wirkleistung P einer zeitlich veränderlichen periodischen
Augenblicksleistung p(t) ist
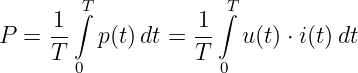 | (9.7.7) |
Die nicht sinusförmigen Spannung u(t) kann mit einer Fourierreihe
nach Gln. 9.3.10 approximiert werden zu
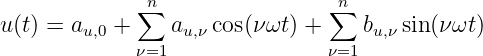 | (9.7.8) |
und ebenso der Strom
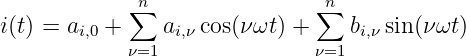 | (9.7.9) |
Eingesetzt in die Gleichung der Wirkleistung ergibt sich
-
Vereinfachung:
-
Mit den Orthogonalitätsrelationen der trigonometrischen
Funktionen (Gln. 9.4.7) ergibt sich wieder vereinfachend
-
Ergebnis:
-
Die Wirkleistung kann direkt aus den Fourierkoeffizienten der
Spannungs- und Stromreihe berechnet werden als Summe der
Gleichleistung, Grundwellenleistung, und Oberwellenleistung
entsprechender Ordnung
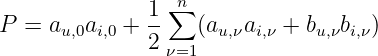 | (9.7.12) |
-
Oder:
-
Anstelle der Fourierkoeffizienten können mit Gln. 9.3.4
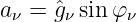
und Gln. 9.3.5
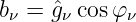
auch die Scheitelwerte und Nullphasenwinkel der Spannungs- und
Stromfunktion verwendet werden
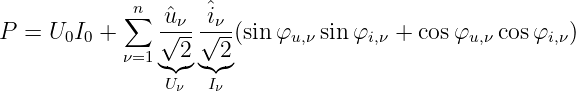 | (9.7.13) |
Mit den Effektivwerten und der trigonometrischen Umrechnung
(Papula, 2006, Seite 94) ergibt sich
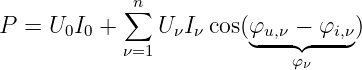 | (9.7.14) |
-
Ergebnis:
-
Die Wirkleistung bei nicht sinusförmigen periodischen Spannungen
und Strömen ist gleich der Summe der Gleichleistung und der
Wechselstromleistung der Grund- und Oberwellen
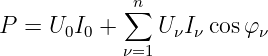 | (9.7.15) |
-
Scheinleistung:
-
Das Produkt der Effektivwerte nach Gln. 9.7.5 von Spannung und
Strom liefert wie bekannt die Scheinleistung
die Aufgrund der Mischterme nicht einfach aus der Addition der
Scheinleistungen der einzelnen Harmonischen berechnet werden
kann.
-
Blindleistung:
-
Auch die Blindleistung
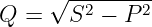 | (9.7.17) |
enthält zusätzliche Mischterme, so dass sich die Blindleistung aus der
Addition der Blindleistungen der einzelnen Harmonischen
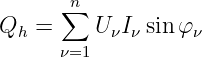 | (9.7.18) |
und entsprechend den Mischtermen einer zusätzlichen
Verzerrungsblindleistung Qd zusammensetzt.
-
Leistungsfaktor:
-
Wir erweitern jetzt noch den aus der Wechselstromtechnik bekannten
Leistungsfaktor für Ströme und Spannungen in Fourierreihen und
erhalten mit
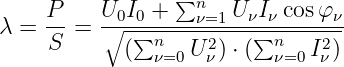 | (9.7.19) |
den allgemeinen Fall, bei dem eine reine Wechselspannung mit der
ersten Harmonischen (k = 1, f = 50Hz) nur ein Sonderfall
ist
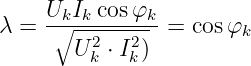 | (9.7.20) |
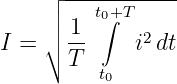
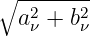 der ν-ten
Teilschwingung entsprechend Gln. 9.3.6
der ν-ten
Teilschwingung entsprechend Gln. 9.3.6
![┌ -----------------------------------
││ t0+∫T [ n ]2
I = │∘ -1 ¯i + ∑ ˆi sin (ν ωt + φ ) dt
T ν=1 ν ν
t0](gde_2295x.png)
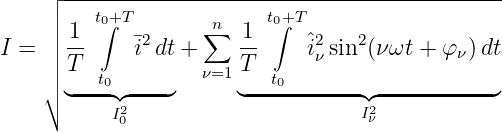
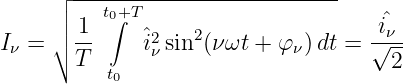
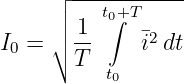
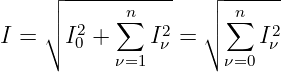
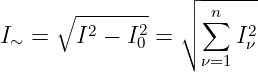
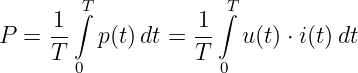
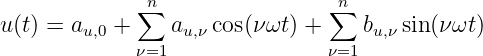
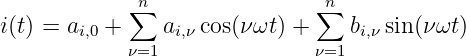
![∫T [ n∑ ∑n ]
P = 1- au,0 + au,ν cos(νωt) + bu,ν sin (ν ωt) ⋅
T 0 ν=1 ν=1
[ n n ]
a + ∑ a cos(νωt) + ∑ b sin(ν ωt) dt
i,0 ν=1 i,ν ν=1 i,ν
(9.7.10)](gde_2304x.png)
![∫T[ n
P = 1- a a + ∑ a a cos2(νωt )
T u,0 i,0 ν=1 u,ν i,ν
0 n ]
∑ 2
+ bu,νbi,ν sin (ν ωt) dt
[ νn=1 n ]
= 1- a a T + ∑ a a T-+ ∑ b b T-
T u,0 i,0 ν=1 u,ν i,ν 2 ν=1 u,ν i,ν2
(9.7.11)](gde_2305x.png)