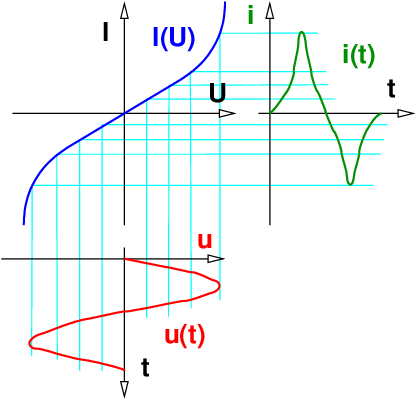
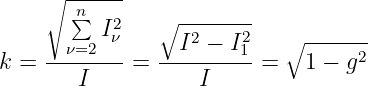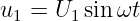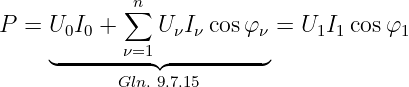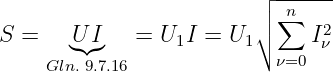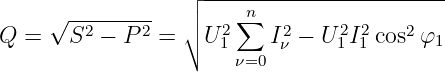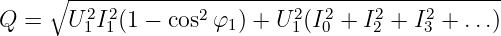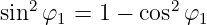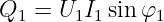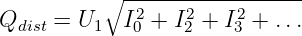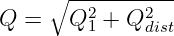Verzerrungen

9.8 Verzerrungen

Praxis NT:

Der Klirrfaktor⁶ erfasst den unerwünschten Einfluss einer nichtlinearen Schaltung auf den Strom bei einer sinusförmigen Wechseleingangsspannung:

Verstärker
Analog-Digital-Umsetzer
Lautsprecher / Mikrofon

→ Anwendung in der Nachrichtentechnik

Praxis AT:

Die Verzerrungsblindleistung⁷ erfasst den unerwünschten Anteil der Blindleistung, die in einem Wechselnetz durch einen nichtlinearen Verbraucher bei einer sinusförmigen Wechseleingangsspannung entsteht:

Gleichrichter in Netzteilen
Wechselrichter
Magnetische Sättigung in Spulen bei Motoren

→ Anwendung in der Automatisierungstechnik

9.8.1 Lineare Verzerrungen

Linear:

In einer linearen Schaltung mit linearen Bauelementen Widerstand R = const, Kondensator C = const und Spule L = const, die Ein- und Ausgangsgrößen unterschiedlicher Kurvenformen aufweisen, spricht man von linearen Verzerrungen. Dabei gilt dass

die Ausgangsgröße nur harmonische Anteile enthält, die schon in der Eingangsgröße enthalten sind,
die Kurvenform der Ausgangsgröße sich nicht ändert, wenn man die Eingangsgröße bei gleich bleibender Kurvenform vergrößert oder verkleinert und
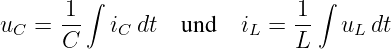
die Amplituden der harmonischen Oberwellen aufgrund der Integration an Kondensator und Spule $1 ∫ 1 ∫ uC = -- iC dt und iL = -- uL dt C L$
oder der Differentiation an Kondensator und Spule
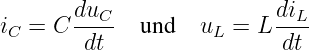
$du di iC = C --C- und uL = L --L- dt dt$
nichtlinear verändert werden.

Widerstand:

Ein Widerstand verändert die Kurvenform nicht.

Spule:

Fließt ein Strom in Form einer Fourierreihe durch die Spule, so wird die Amplitude der ν-te Teilschwingung der Spannung an der Spule mit Differentiation zu

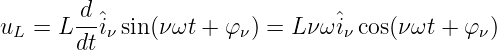d uL = L --ˆiν sin(νωt + φν) = L νωˆiν cos(νωt + φν) dt

(9.8.1)

→ Multiplikation der Teilschwingungsamplitude û_L mit νω wodurch höherfrequente Anteile verstärkt werden.

Kondensator:

Fließt ein Strom in Form einer Fourierreihe durch den Kondensator, so wird die Amplitude der ν-te Teilschwingung der Spannung am Kondensator mit Integration zu

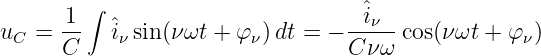∫ ˆ uC = -1 ˆiν sin(νωt + φ ν) dt = −-iν--cos(νωt + φν) C Cν ω

(9.8.2)

→ Division der Teilschwingungsamplitude û_C durch νω wodurch höherfrequente Anteile gedämpft werden.

9.8.2 Nichtlineare Verzerrungen

Verzerrung:

In einer nichtlinearen Schaltung treten trotz sinusförmiger Spannung u(t) nicht sinusförmige Ströme i(t) auf. In Abb. 9.8.1 ist beispielhaft die Kennlinie eines nichtlinearen Widerstandes dargestellt. Weitere nichtlineare Bauelemente sind Gleichrichter, stromabhängige Induktivitäten oder Dioden und Transistoren.

Abbildung 9.8.1: Stromverzerrung an einem nichtlinearen Bauelement bei Sinusspannung

Definition:

Der Schwingungsgehalt (s) einer Mischgröße wird nach DIN 40110 für einen Strom (s_i) definiert als Quotient der Effektivwerte von Wechselanteil und Gesamtgröße⁸

I∼ s = si = --- I

(9.8.3)

mit dem Effektivwert des Wechselstromanteils entsprechend Gln. 9.7.6

┌ ------ ∘ -2----2 ││ ∑n 2 I∼ = I − I0 = ∘ Iν ν=1

1. FRAGE:

Was war noch einmal eine Mischgröße?

2. FRAGE:

Wie groß ist der Schwingungsgehalt einer Wechselgröße?

Speziell:

Für reine Wechselgrößen ist der Gleichanteil I₀ = 0 und somit wird I_∼ = I. Damit hat der Schwingungsgehalt keine Aussage mehr und man definiert stattdessen den Grundschwingungsgehalt als Quotienten der Effektivwerte von Grundschwingung und der gesamten Wechselgröße

g = I1-= I1 I∼ I

(9.8.4)

Definition:

Als Oberschwingungsgehalt oder Klirrfaktor einer Wechselgröße bezeichnet man den Quotienten aus dem Effektivwert aller Oberschwingungen (für ν ≥ 2) und der gesamten Wechselgröße