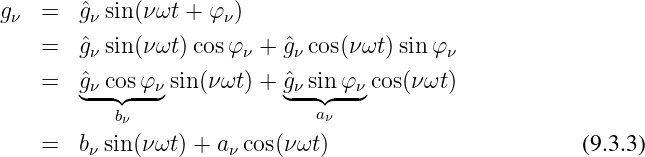9.3 Fourierreihen

Spektralform:

Jede beliebige periodische Funktion f(t) kann durch eine endliche Fourierreihe²

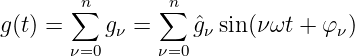(9.3.1)

mit dem Gleichanteil g₀ = ĝ₀ sin φ₀ und den Amplituden ĝ_ν und Nullphasenwinkeln φ_ν der harmonischen Oberwellen beliebig genau dargestellt werden.

→ Diese Darstellung wird als Spektralform der Fouriereihe bezeichnet.

→ Die Gliederzahl n bestimmt die Güte der Näherung, sie ist um so besser, je größer n ist.

Einschränkung:

Die Funktion f(t) muss außerdem die Dirichletschen Bedingen erfüllen:

1. Die Funktion ist endlich³ und
2. das Intervall [0, 2π] lässt sich in endlich viele Teilintervalle zerlegen, in denen f(t) stetig und monoton ist.

Koeffizienten:

Die Koeffizienten ĝ_ν der Fourierreihe müssen so bestimmt werden, dass das Fehlerintegral

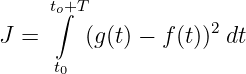(9.3.2)

minimal wird.

→Mathematik: Differenzieren nach den Koeffizienten und Nullsetzen der 1. Ableitung!

Alternativ:

Mit dem Additionstheorem (Papula, 2006, Seite 94)⁴

ergeben sich Koeffizienten der Fourierreihe für reine Kosinusterme

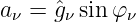(9.3.4)

und Koeffizienten für reine Sinusterme

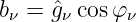(9.3.5)

Zurück:

Umgekehrt lassen sich die Amplitude

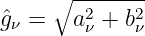(9.3.6)

und der Phasenwinkel

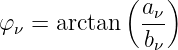(9.3.7)

aus den Koeffizienten der Kosinus- und Sinusterme berechnen.

Normalform:

Die Fourierreihe wird dann zu

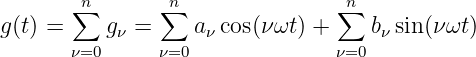(9.3.8)

Mit dem Gleichanteil für ν = 0

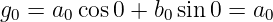(9.3.9)

ergibt sich die Normalform der Fourierreihe zu

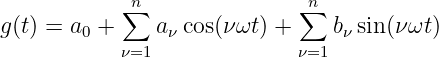(9.3.10)

Näherung:

Zur Approximation der Originalfunktion f(t) durch die Näherungsfunktion g(t) müssen beide Funktionen dieselbe Periodendauer T aufweisen.

→ Es dürfen nur sinusförmige Funktionen verwendet werden, deren Frequenz ein ganzzahliges Vielfaches der Grundfrequenz ist.