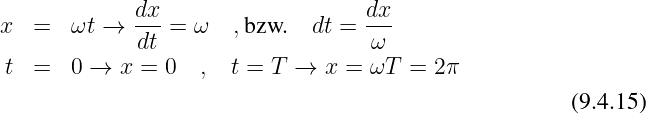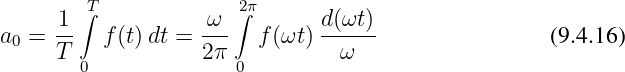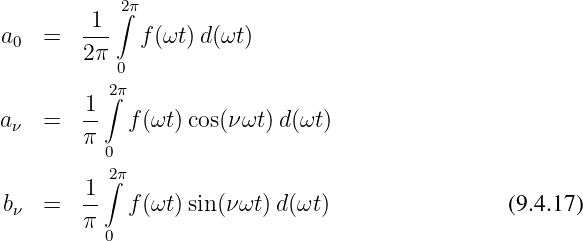Fourieranalyse

9.4 Fourieranalyse

Definition:

Die Zerlegung einer periodischen Funktion in einzelne sinusförmige Teilschwingungen wird als Fourieranalyse bezeichnet.

→ Das Ergebnis der Fourieranalyse sind die Koeffizienten der Fourierreihe.

Mathematik:

Da die Fourierreihe nach Gln. 9.3.10 eine Linearkombination der Koeffizienten ist, kann Gln. 9.3.2 mit der Kettenregel nach den Koeffizienten differenziert werden.

→ Differenzieren nach den Konstanten a_ν, wobei ν = 0 für den Koeffizienten a₀ steht, ergibt

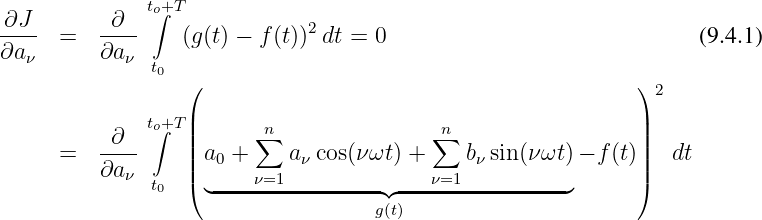
to∫+T -∂J- = -∂-- (g(t) − f(t))2dt = 0 (9.4.1) ∂a ν ∂aν t0 ( ) 2 to∫+T|| ∑n ∑n || = -∂-- || a0 + aν cos(ν ωt) + bν sin(νωt) − f (t)|| dt ∂aν |( ν=1 ν=1 |) t0 ◟----------------◝◜---------------◞ g(t)

→ Verfährt man ebenso für die b_ν so erhält man 2n + 1 Gleichungen für die 2n + 1 Fourierkoeffizienten.

Kette:

Mit der Kettenregel der Differentialrechnung (y = F(u(x)) ergibt y′ = F′(u) ⋅ u′(x)) ergibt sich für den Koeffizienten a₀

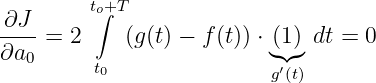to+∫T ∂J--= 2 (g(t) − f(t)) ⋅ (1) dt = 0 ∂a0 ◟◝◜◞ t0 g′(t)

(9.4.2)

und für die anderen Koeffizienten a_ν

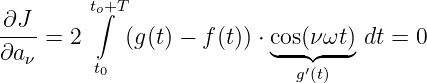∂J to∫+T ----= 2 (g(t) − f (t)) ⋅ cos(νωt) dt = 0 ∂a ν t0 ◟ g◝′◜(t) ◞

(9.4.3)

Summe:

Mit der Summenregel der Differentialrechnung ergibt sich nach dem Trennen der Integrale für den Koeffizienten a₀

to∫+T to+∫T ∑n f (t) dt = [a0 + aμ cos(μωt) t0 t0 μ=1 ∑n + bμ sin(μωt )]dt (9.4.4) μ=1

und für die anderen Koeffizienten a_ν

t∫o+T to+∫T ∑n f(t)cos(νωt) dt = [a0 + aμ cos(μωt) t0 t0 μ=1 ∑n + bμ sin(μωt )]cos(ν ωt)dt μ=1 (9.4.5)

Rechts:

Für die Integrale auf der rechten Seite gilt entsprechend den Orthogonalitätsrelationen der trigonometrischen Funktionen

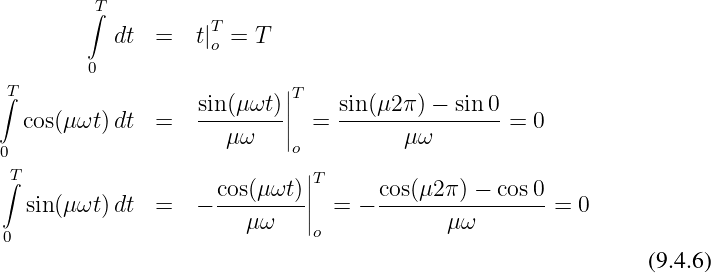
T∫ dt = t|T = T o 0 | ∫T sin(μωt)||T sin(μ2 π) − sin 0 cos(μ ωt)dt = --------|| = ----------------= 0 0 μω o μω ∫T ||T sin(μ ωt)dt = − cos(μωt)-|| = − cos(μ2-π)-−-cos0 = 0 μω |o μω 0 (9.4.6)

und

∫T { cos(μωt) cos(ν ωt)dt = T ∕2 für μ = ν 0 für μ ⁄= ν 0 ∫T { T ∕2 für μ = ν sin(μωt )sin (ν ωt)dt = 0 0 für μ ⁄= ν (9.4.7)

und

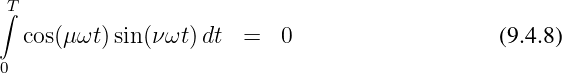
∫T cos(μωt)sin(νωt )dt = 0 (9.4.8) 0

→ Die Integrale mit den Sinustermen werden für die analoge Berechnung der b_ν benötigt.

Gleichungen:

Es ergibt sich das vereinfachte Gleichungssystem

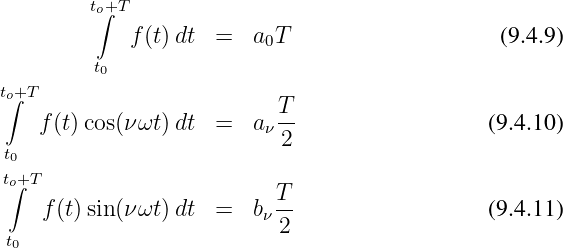
to+∫T f(t)dt = a T (9.4.9) 0 t0 to∫+T T f(t)cos(ν ωt)dt = aν-- (9.4.10) t0 2 to+T ∫ T- f (t) sin(ν ωt)dt = bν2 (9.4.11) t0

a₀:

Somit erhalten wir den Gleichanteil a₀ der Funktion f(t) zu

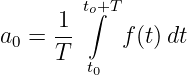to∫+T a = 1- f(t)dt 0 T t0

(9.4.12)

a_ν:

Ebenso werden die Fourierkoeffizienten a_ν der Funktion f(t) zu

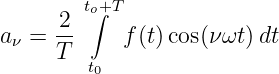to+∫T a = -2 f(t)cos(νωt )dt ν T t0

(9.4.13)

b_ν:

Und die Fourierkoeffizienten b_ν der Funktion f(t) sind damit

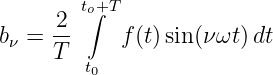to+∫T -2 bν = T f(t)sin(νωt) dt t0

(9.4.14)

Sonderfall:

Bei periodischen Funktionen mit besonderen Symmetrieeigenschaften werden einige der Koeffizienten der Fourierreihe zu Null:

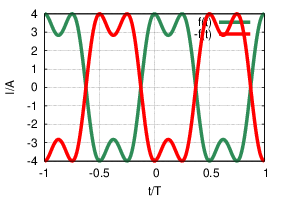
Gerade␣Funktion mit f(−t) = f(t) (siehe Abb. 9.4.1)
→Spiegelsymmetrisch zur y-Achse (Achsensymmetrie)
Ungerade␣Funktion mit f(−t) = −f(t) (siehe Abb. 9.4.1)
→Zentralsymmetrisch zum Ursprung (Punktsymmetrie)
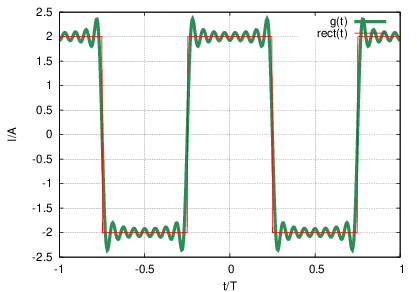
Wechselfunktion mit f(t) = 0 (siehe Abb. 9.4.2)
→Gleichanteil ist Null
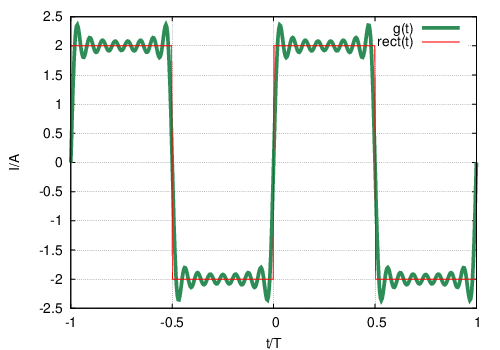
Alternierende␣Funktion f(t + T∕2) = −f(t) (siehe Abb. 9.4.2)
→ Form der positiven und negativen Halbschwingung gleich. (Tabelle: x = Koeffizienten von gradzahligen Vielfachen der Grundfrequenz sind Null.)


Funktion	Graph	Bedingung	Koeffizienten


			a₀	a_ν	b_ν


Gerade (wie cos)		f(−t) = f(t)			0

Ungerade (wie sin)		f(−t) = −f(t)		0

Abbildung 9.4.1: Sonderfälle der Fourieranalyse: Gerade und Ungerade Funktion


Funktion	Graph	Bedingung	Koeffizienten


			a₀	a_ν	b_ν


Wechsel		f(t) = 0	0

Alter- nierend		f(t + T∕2) = −f(t) (rot: -f(t))	0	x	x

Abbildung 9.4.2: Sonderfälle der Fourieranalyse: Wechsel- und alternierende Funktion

Beispiel 9.4.1 (Fourierkoeffizienten)

Welche Koeffizienten sind Null für die symmetrische Rechteckschwingung in Abb. 9.4.3 mit dem Tastverhältnis 1∕2?

Abbildung 9.4.3: Fourieranalyse einer rechteckförmigen Stromfunktion

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Es handelt sich um eine

Wechselfunktion
Gerade Funktion
Alternierende Funktion

Abbildung 9.4.4: Näherungsfunktion einer rechteckförmigen Stromfunktion

Für die Darstellung in Abb. 9.4.4 wurden ungerade Koeffizienten der Kosinusfunktionen bis n = 15 verwendet. Die Berechnung der Koeffizienten sei zur Übung empfohlen.

Beispiel 9.4.2 (Fourierkoeffizienten)

Es sind die Fourierkoeffizienten der Rechteckfunktion in Abb. 9.4.5 für eine zeitliche Verschiebung um Δt = T∕4 zu berechnen!

Abbildung 9.4.5: Fourieranalyse einer verschobenen rechteckförmigen Stromfunktion

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

ˆ b2ν−1 = 4i ⋅---1--- , ν = 1,2,3,... π---2ν-−-1-

Substitution:: Bei der Berechnung der Fourierkoeffizienten nach Gln. 9.4.12-9.4.14 kann statt nach dt mit folgender Substitution auch direkt nach dx = d(ωt) integriert werden
$x = ωt → dx- = ω ,bzw. dt = dx- dt ω t = 0 → x = 0 , t = T → x = ωT = 2π (9.4.15)$
z.B. für
$∫T 2∫π a0 = 1- f (t) dt = ω-- f(ωt ) d(ωt) (9.4.16) T 2π ω 0 0$
mit dem Ergebnis
$2∫π a = -1- f(ωt) d(ωt) 0 2 π 0 1∫2π a ν = -- f(ωt)cos(ν ωt)d(ωt) π 0 ∫2π b = -1 f(ωt)sin(νωt )d(ωt) (9.4.17) ν π 0$

[next] [prev] [prev-tail] [front] [up]