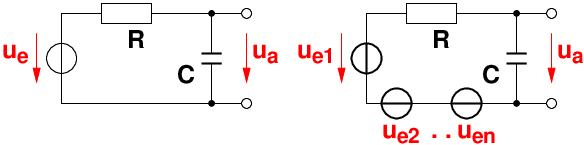[next] [prev] [prev-tail] [tail] [up]

9.1 Sinusförmige Zeitfunktionen

Verfahren:

Für die Normalform der Fouriereihe nach Gln. 9.3.10

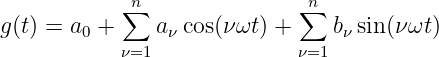
∑n ∑n g(t) = a0 + aν cos(νωt) + bν sin(νωt ) ν=1 ν=1

erhalten wir den Gleichanteil mit Gln. 9.4.12

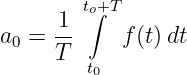
to∫+T a = 1- f(t)dt 0 T t0

und die Fourierkoeffizienten mit Gln. 9.4.13 zu

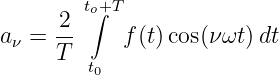
to+∫T a = -2 f(t)cos(νωt )dt ν T t0

und mit Gln. 9.4.14 zu

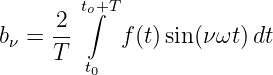
2 to+∫T bν = -- f(t)sin(νωt) dt T t0

Frage:

Warum kann man die periodische Zeitfunktion f(t) durch die Summenfunktion g(t) ersetzen und warum sollte man das machen?

Vorteil:

Die Zerlegung von nicht sinusförmigen Wechselgrößen in sinusförmige Teilschwingungen ermöglicht es, bekannte Verfahren der bisherigen Netzwerkanalyse weiter zu verwenden1.

PIC

Abbildung 9.1.1: Reihenschaltung sinusförmiger Quellen unterschiedlicher Frequenzen
Linear:

In linearen Schaltungen kann dann die nicht sinusförmige, periodische Wechselgröße ue am Eingang einer Schaltung entsprechend Abb. 9.1.1 als Überlagerung der Sinusquellen uei,i = 1,n dargestellt werden.

→ Netzwerkanalyse mit dem Verfahren der Superposition: Die Ausgangsspannung ergibt sich dann als Überlagerung der Sinusspannungen uai,i = 1,n.

Beispiel 1:

Addition von zwei Kosinusspannungen

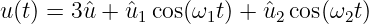u(t) = 3 ˆu + ˆu1cos(ω1t) + ˆu2cos(ω2t)
(9.1.1)

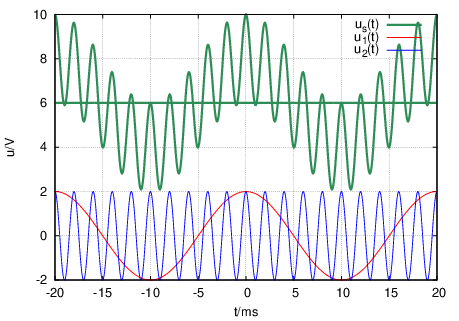
mit û = û1 = û2 und ω2 = 10ω1. Die Summenspannung enthält eine niederfrequente Grundschwingung, die mit der höherfrequenten Schwingung moduliert ist. Zur Verdeutlichung enthält das Summensignal den zusätzlichen Gleichanteil.

PIC

Abbildung 9.1.2: Addition sinusförmiger Spannungen unterschiedlicher Frequenzen mit ω2 ≫ ω1
Beispiel 2:

Addition von zwei Kosinusspannungen

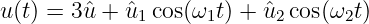u(t) = 3 ˆu + ˆu1cos(ω1t) + ˆu2cos(ω2t)
(9.1.2)

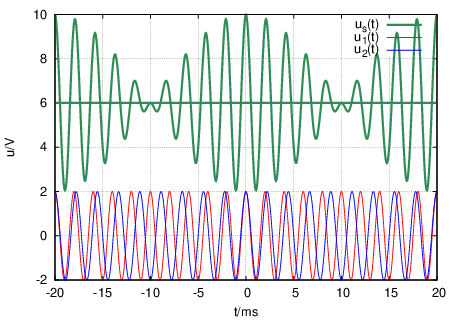
mit û = û1 = û2 und ω2 = 0.9ω1. Die Summenspannung ist eine Schwebung, bei der die Amplitude zwischen (û1 + û2) und (im allgemeinen Fall) (û1 −û2) schwingt. Zur Verdeutlichung enthält das Summensignal wieder den zusätzlichen Gleichanteil.

PIC

Abbildung 9.1.3: Addition sinusförmiger Spannungen unterschiedlicher Frequenzen mit ω2 ≈ ω1
Mathematik:

Mit dem Additionstheorem (Papula, 2006, Seite 96)

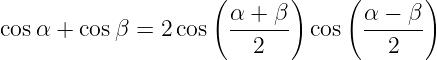(α + β) (α − β) cosα + cosβ = 2cos ------ cos ------ 2 2
(9.1.3)

erhalten wir für die Addition der beiden Kosinusspannungen

u(t) = uˆ1 cos(ω1t) + ˆu2cos(ω2t) + 0 = uˆ1 cos(ω1t) + ˆu2cos(ω2t) + [ˆu◟1-−-ˆu1◝]◜cos(ω2t)◞ 0 = uˆ1 [cos(ω1t) + cos(ω2t)] + [ˆu2 − ˆu1]cos(ω2t) ( ω + ω ) (ω − ω ) = 2 ˆu1cos -1-----2t cos --1----2t 2 2 + [ˆu2 − ˆu1]cos(ω2t) (9.1.4)
Spezialfall:

Der spezielle Fall, das die Frequenzen in einem ganzzahligen Vielfachen stehen

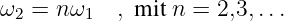ω2 = nω1 , mit n = 2,3,...
(9.1.5)

führt zur Überlagerung harmonischer Schwingungen, mit Grund- und Oberschwingungen, die von zentraler Bedeutung sind.

1Für eine Sinusspannung ist die Lösung zu Abb. 9.1.1 in GdE 1 behandelt worden! In Aufgabe 9.10.5 wird dieser Tiefpass für eine Dreieckseingangsspannung berechnet.

[next] [prev] [prev-tail] [front] [up]