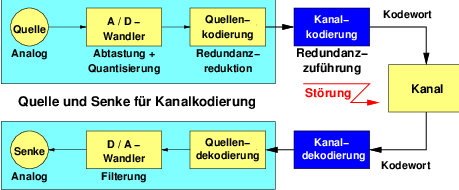
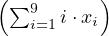Kanalkodierung

7.2 Kanalkodierung

Kodierung:

Die Kanalkodierung ist eine Kodierung zur Erkennung und / oder Korrektur von Übertragungsfehlern durch einen gestörten Kanal.

Abbildung 7.2.1: Kommunikationsstrecke mit Kanalkodierung

→ Im englischen heisst es besser Error Control Coding, was die Beherrschung der Fehler ausdrückt — ein Vermeiden von Übertragungsfehlern ist nicht möglich.

→ Erhöhung der Redundanz, d.h. Übertragung zusätzlicher Daten, die keine Nutzdaten enthalten.

Strategien:

Es gibt 2 sich ergänzende Strategien:

Bei der Forward Error Correction (FEC) erfolgt eine Fehlerkorrektur im Empfänger.
→ Echtzeit, z.B. UDP für Voice over IP
Beim Automatic Repeat Request (ARQ) erfolgt auf eine Fehlererkennung im Empfänger eine Wiederholungsanforderung an den Sender.
→ Datenübertragung, z.B. TCP beim FTP

Qualität:

Das Qualitätsmaß einer digitalen Übertragung ist die (gemessene) Bitfehlerrate (BER, Bit Error Rate) oder die (theoretische) Bitfehlerwahrscheinlichkeit.

→ Der Kodierungsgewinn durch die Kanalkodierung ermöglicht theoretisch eine beliebig kleine Bitfehlerrate.

Kosten:

Kompromiss zwischen: Komplexität (Kosten) — Datendurchsatz — Fehlererkennungs- und -korrekturvermögen.

Klassen:

Bei binären Kodes ist das Rechnen in so genannten Restklassenkörpern erforderlich

Ein Körper ist eine Menge G, deren Elemente addiert, subtrahiert, multipliziert und dividiert werden können, so dass das Resultat immer wieder ein Element der Menge ist.
Die Addition und die Multiplikation müssen das Kommutativ-, das Assoziativ- und das Distributivgesetz erfüllen.
Ein Restklassenkörper modulo p (mod_p) besteht aus der Menge der natütlichen Zahlen G = {0, 1, 2,...,p − 1}⁸.

Beispiel:

Für p = 2 erhalten wir G = {0, 1} mit den Operationen XOR für die Addition und AND für die Multiplikation:⁹


	XOR: ⊕		AND: ⊗

	0	1	0	1


0	0	1	0	0

1	1	0	0	1

Parity:

Bei der Paritätsprüfung (Parity Check) werden Paritätsbits zusätzlich eingefügt, die die Anzahl der Einsen (oder Nullen) ergänzen, zur Erkennung von 1-Bit-Fehlern

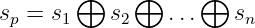⊕ ⊕ ⊕ sp = s1 s2 ... sn

(7.2.1)

Kontrolle beim Empfänger mit

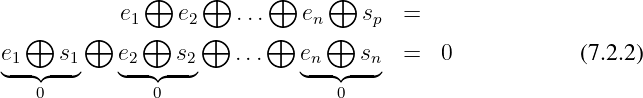
e ⊕ e ⊕ ...⊕ e ⊕ s = ⊕ ⊕ 1⊕ 2⊕ ⊕ n⊕ p e1 s1 e2 s2 ... en sn = 0 (7.2.2) ◟--◝◜-◞ ◟--◝◜--◞ ◟---◝◜--◞ 0 0 0

Eigenschaften:

Hier wird Even Parity mit einer gerade Anzahl 1 erzeugt
Alternativ Odd Parity mit einer ungerade Anzahl 1
Es kann eine ungerade Anzahl von Übertragungsfehler erkannt aber nicht korrigiert werden.

Frage:

Wie kann das Verfahren erweitert werden, um 1 Bit Übertragunsfehler korrigieren zu können? Geht das überhaupt?

Block:

Zur Erkennung und Korrektur von 1-Bit-Fehlern wird ein Datenblock aus n Zeilen mit je m Datenbits je Zeile mit einem Prüfbit mit einer zusätzlichen Prüfzeile für die m Spalten gesichert, wie es in Abb. 7.2.2 dargestellt ist .

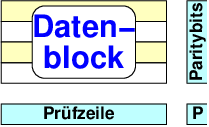
1-Bit-Fehler im Block lokalisierbar
Prüfbit P ist Parity für Datenblock
Prüfbitfehler sind feststellbar

Abbildung 7.2.2: Prinzipieller Aufbau eines Parity-Blockkodes

Eigenschaften:

Über die n-m-Blockgröße der Daten kann das Verfahren an die Bitfehlerwahrscheinlichkeit des Kanals angepasst werden.
Aufgrund des zusätzlichen Prüfbits lassen sich beliebiege 2-Bitfehler noch erkennen, wobei sonst je ein Fehler in der Prüfspalte und der Prüfzeile zu einer Korrektur eines richtigen Datenbits führen würde.

Sicherheit:

Ein Maß für die Störsicherheit eines Kodes ist die Hammingdistanz des Kodes.

Mit der (Hamming-) Distanz (oder dem Abstand) d = d(x,y) wird die Anzahl unterschiedlicher Zeichen der Kodewörter x und y bezeichnet.

Minimum:

Die Hammingdistanz h des Kodes ist das Minimum der Abstände d_min zwischen zwei beliebigen Kodewörtern eines Kodes.

Bei h = d_min können (d_min − 1)-Zeichenfehler erkannt werden und vom Sender neu angefordert werden (ARQ).
Bei h = d_min können (d_min − 1)∕2- Zeichenfehler vom Empfänger selbständig korrigiert werden (FEC).
Es gilt immer h ≥ 1, da sonst 2 Kodewörter gleich sind.
Bei h = 1 können i.a. 1-Bit-Zeichenfehler nicht erkannt werden, da schon ein Übertragungsfehler zu einem gültigen anderen Kodewort führen kann.¹⁰

Beispiel 7.2.1 (ISBN-13)

Berechnen Sie für den ISBN (International Standard Book Number) Prüfziffernkode¹¹ die Prüfziffer für den ISBN-13 → Kanalkodierung¹²
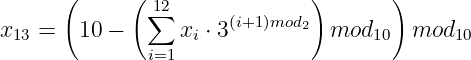
$( ( ) ) 1∑2 (i+1)mod2 x13 = 10 − xi ⋅ 3 mod10 mod10 i=1$ (7.2.3)

für die 13-stellige ISBN-Nummer¹³ ₁ −₂ −₃ −₄ −₅
→ Der Kode erkennt einen Fehler an einer beliebigen Stelle (Hammingdistanz h = 2) und zudem noch Zahlendreher an zwei benachbarten Stellen .
Berechnen Sie dann für den 13-stelligen Code die Prüfziffer nach demgleichen Verfahren!

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Zahlenwerte sind:

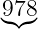
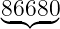
Prüfziffer für ISBN 978-3-86680-192-?
$x13 = 9-$
Prüfziffer für ISBN 978-3-86680-192-9
$x13 = 0-$

Praxis:

Bei den Cyclic-Redundancy-Check-Kodes (CRC) werden die (n+1) Bits a_i der Nachricht als Koeffizienten a_ixⁱ eines Polynoms n-ten Grades aufgefasst. Die Modulo-2-Division durch ein Generatorpolynom vom Grad r ergibt die Prüfbits.

CRC-Algorithmus:

Die (n+1) Bits des Datenwortes W(x) sind die Koeffizienten des Polynoms PW(x) des Grades n.
Durch Multiplikation PW′(x) = PW(x) ⋅ x^r wird W(x) um r Nullen ergänzt.
Wird PW′(x) durch das Generatorpolynom PG(X) vom Grad r mod-2-dividiert ergibt sich das Restpolynoms PR(x).
Als Kodewort wird S(x) = W′(x) − R(x) über den Übertragungskanal zum Empfänger geschickt.
Der Empfänger mod-2-dividiert diese Daten durch das Generatorpolynom und erhält den Restfehler PS′(x) = 0 bei fehlerfreier Übertragung.

Beispiel 7.2.2 (CRC)

Generatorpolynom PG(x) = 1⋅x⁴+1⋅x³+0⋅x²+0⋅x¹+1⋅x⁰
Generatorwort G(x) = 11001
(n + 1) = 8, Datenwort W(x) = 10100011
n = 7, Datenpolynom PW(x) = x⁷ + x⁵ + x + 1
Neues Datenwort mit (r=4) Nullen W′(x) = 101000110000

Berechnen Sie die folgenden beiden Polynomdivisionen:

Polynomdivision¹⁴ im Sender liefert das Sendewort
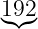
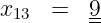
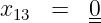
$R (x) = [W ′(x)∕G (x)]mod2 = [101000110000 ∕11001 ]mod2 (7.2.4)$
Polynomdivision im Empfänger liefert den Übertragunsfehler
$′ ′ S (x) = [(W (x) − R (x))∕G (x )]mod2 = [101000111010 ∕11001 ]mod2 (7.2.5)$

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Zahlenwerte sind:

Polynomdivision:

1 0 1 0 0 0 1 1 0 0 0 0 / 1 1 0 0 1 = 1 1 0 0 1 0 1 0
1 0 1 0 = R e s t
Polynomdivision:

1 0 1 0 0 0 1 1 1 0 1 0 / 1 1 0 0 1 = 1 1 0 0 1 0 1 0
0 0 = R e s t

Kodeklassen:

Bei den Tetraden-Kodes können die Pseudo-Tetraden als Fehler erkannt werden
→ Binäry Kodes Decimal (BCD-Kode) mit 4 binären Zeichen für jede der 10 Dezimalziffern.
Bei den m-aus-n-Kodes handelt es sich um Blockkodes mit der Länge n, bei denen in jedem Kodewort genau m-Einsen enthalten sind
→ 2-aus-5-Kode: 0 → 00011, 1 → 00101, …¹⁵
→ 1-aus-10-Kode: 0 → 0000000001, 1 → 0000000010, …¹⁶
Bei den Ziffernkodes handelt es sich um fehlertolerante Kodes, bei denen 1-Bit-Fehler zu benachbarten Zahlen (des Quellalphabets) führen
→ Vierstelliger Gray-Kode für die Ziffern 0… 9, z.B. wird aus der 6 (1111) die 5 (1110), die 7 (1101) oder ein Fehler (0111 und 1011).

Von Linearen Kodes spricht man, wenn das Alphabet des Kodes so gewählt wird, dass es durch Einführen geeigneter Operationen zu einem linearen Raum (Vektorraum, Galois-Körper → Methoden der linearen Algebra) wird.

Die Zyklischen Kodes bilden eine Untermenge der Linearen Kodes mit der zusätzlichen Eigenschaft, dass jede zyklische Verschiebung eines Kodewortes wieder ein gültiges Kodewort ergibt

→ Cyclic Reduncy Check Kodes (CRC, auch Frame Check Sequence, FCS), die mit einem (genormten) Generatorpolynom aus einem primitiven Polynom P(x) erzeugt werden: G(x) = (x + 1) ⋅ P(x). Zwei genormte Generatorpolynome sind z.B.¹⁷


Kode	Generatorpolynom G(X)	Anwendung


CRC-4	x⁴ + x¹ + x⁰ = x⁴ + x + 1	ISDN

CRC-8	(x + 1)(x⁷ + x⁶ + x⁵ + x⁴ + x³ + x² + 1)	ATM
	= x⁸ + x² + x + 1

⁸Vektorraum, Galois-Körper mit Methoden der linearen Algebra

⁹Da 1⊕ 1 = 0 ist folgt −1 = 1. Es gibt also keine Vorzeichenfehler!

¹⁰Ausnahme: Redundanz in den Kodeworten, z.B. ungültige Kodeworte beim BCD-Kode.

¹¹Beim EAN-13 (European Article Number) Produktkode wird dieselbe Kanalkodierung verwendet!

¹²Prüfziffer für ISBN-10 ist x₁₀ = (∑ )
9i=1 i⋅xi mod₁₁ mit X = 10 für Rest 10.

¹³(1) Präfix bei ISBN-13, (2) Gruppe, z.B.: 3 deutschsprachig, (3) Verlag, (4) Titel, (5) Prüfziffer

¹⁴Mit Hilfe der Modulo-2-Subtraktion. Die Polynomdivision wird in der Praxis durch ein IIR-Filter als rückgekoppeltes Schiebregister realisiert.

¹⁵Es gibt „5-über-2“ = 5! / (5-2)! 2! = 10 mögliche Kodewörter.

¹⁶Es gibt „10-über-1“ = 10! / (10-1)! 1! = 10 mögliche Kodewörter.

¹⁷Bei CRC-4 sind 4 aufeinanderfolgende Bündelfehler detektierbar, bei CRC-8 entsprechend 8 Bündelfehler (Fehler in aufeinander folgenden Bits).

[next] [prev] [prev-tail] [front] [up]