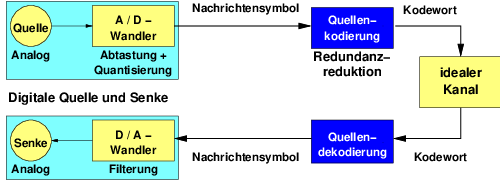
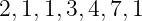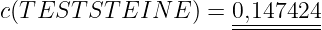Quellenkodierung

7.1 Quellenkodierung

Ziel:

Das Ziel einer Quellenkodierung wie in Abb. 7.1.1 ist die zu übertragenden Nachrichtensymbole möglichst optimal in eine Folge von Zeichen zu kodieren.¹

Abbildung 7.1.1: Kommunikationsstrecke mit Quellenkodierung

→ Verlustfreie Datenkompression mit Reduzierung der Redundanz erfolgt ohne Informationsverlust.

→ Verlustbehaftete Datenkompression mit Reduzierung der Irrelevanz (nicht benötigter Teil der Information) ergibt Informationsverlust.

Definition:

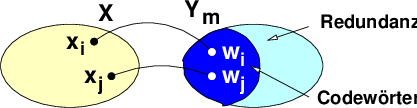
Als Kodierung (siehe auch Abb. 7.1.2) bezeichnet man eine injektive Abbildung, die jedem Zeichen x einer Quelle X ein Kodewort c zuordnet²

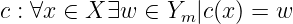c : ∀x ∈ X ∃w ∈ Y |c(x) = w m

(7.1.1)

→ Injektiv: Aus c(x₁) = c(x₂) folgt x₁ = x₂.

Kodewort:

Y = {y₁,…y_r} ist dabei ein weiteres Alphabet und w ∈ Y Y … = Y ⁱ ein Wort des Alphabets mit der Menge aller Worte

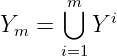m⋃ Ym = Yi i=1

(7.1.2)

Abbildung 7.1.2: Kodierung als injektive Abbildung von X in Y _m

Wortlänge:

Die mittlere Wortlänge einer Kodierung kann aus der einzelnen Länge der Kodewörter l(w_i) = l_i bestimmt werden zu

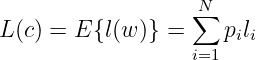N L (c) = E {l(w)} = ∑ pili i=1

(7.1.3)

Das Shannon’sche Kodierungstheorem besagt, dass die mittlere Wortlänge einer Kodierung größer oder bestenfalls gleich der maximalen Entropie der Quelle ist

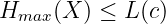H (X ) ≤ L (c) max

(7.1.4)

Effizienz:

Mit der Effizienz eines Kodes c für die Quelle X

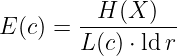H (X ) E (c) = ---------- L(c) ⋅ ld r

(7.1.5)

wird die Redundanz R = L(c) ld(r) − H(X) der Kodierung c erfaßt³, wobei L(c) ld(r) die maximale Entropie des Kodes mit r Buchstaben ist.

Idealer Kode:

Da bei decodierbaren Kodes die gesammte Quelleninformation erhalten bleibt, gibt es einen optimalen oder idealen Kode mit der Effizienz E(c) = 1.

→ Es gibt keinen anderen Kode mit demselben Kodealphabet, der für dieselbe Quelle eine kleinere mittlere Kodelänge aufweist.

Beispiel: 7 Bit ASCII-Kode
N = 2⁷ = 128 Zeichen → L(c) = 7
Kodierung mit r = 2 Zeichen 0, 1 → ld r = ld 2 = 1.
Quellenentropie
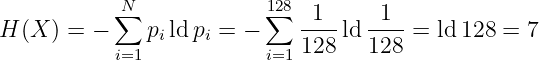
$N∑ 1∑28 H (X ) = − pild pi = − -1--ld -1--= ld 128 = 7 i=1 i=1128 128$
Effizienz des Kodes
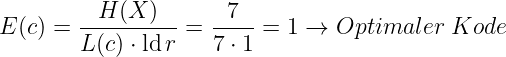
$-H--(X-)--- --7- E (c) = L(c) ⋅ ld r = 7 ⋅ 1 = 1 → Optimaler Kode$
Voraussetzung: Gleiche Wahrscheinlichkeit p_i = 1∕128

Morsezeichen:

Der bekannteste Kode ist das Morsealphabet, das international genormte Telegraphenalphabet⁴. Benannt nach dem Erfinder Samuel Morse (1791 – 1872), der 1838 das Morsealphabet entwickelte für den von ihm 1 Jahr zuvor konstruierten elektromagnetischen Schreibtelegraphen.

Die Länge der Kodes aus Punkten („di“), Strichen („dat“ = 3 „dit“) korreliert mit der Häufigkeit der Buchstaben in der englischen Schriftsprache (siehe auch Tab. 7.1). Als zusätzliche Trennzeichen ist noch die Pause notwendig: einfach zwischen Zeichen (Länge = „dit“), 3-fach zwischen Kodeworten und 6-fach zwischen Worten des Eingangsalphabets.


E	-				16,93	12,60	T	—				5,79	9,37

I	-	-			8,02	6,71	M	—	—			2,55	2,53
A	-	—			5,58	8,34	N	—	-			10.53	6,80

S	-	-	-		6,42	6,11	O	—	—	—		2,24	7,70
U	-	-	—		3,83	2,85	G	—	—	-		3,02	1,92
R	-	—	-		6,89	5,68	K	—	-	—		1,32	0,87
W	-	—	—		1,78	2,34	D	—	-	-		4,98	4,14

H	-	-	-	-	4,98	6,11	CH	—	—	—	—
V	-	-	-	—	0,84	1,06	Ö	—	—	—	-	0,30
F	-	-	—	-	1,49	2,03	Q	—	—	-	—	0,02	0,02
Ü	-	-	—	—	0,65		Z	—	—	-	-	1,21	0,06
L	-	—	-	-	3,60	4,24	Y	—	-	—	—	0,05	2,04
Ä	-	—	-	—	0,54		C	—	-	—	-	3,16	2,73
P	-	—	—	-	0,67	1,66	X	—	-	-	—	0,05	0,20
J	-	—	—	—	0,24	0,23	B	—	-	-	-	1,96	1,54

Tabelle 7.1: Kodierung der Buchstaben im Morsealphabet

Kodebaum:

Kodebäume,wie in Abb. 7.1.3, sind Hilfsmittel zur optischen Verdeutlichung von Kodeeigenschaften

X	p(x_i)	c(x_i)

x₁	0,18	11
x₂	0,15	101
x₃	0,09	100
x₄	0,25	01
x₅	0,33	00

Abbildung 7.1.3: Kodebaum zur Kodierung der Smbole {x₁, …, x₅}

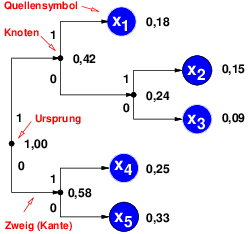
Fano-Bedigung: Kein Kodewort darf das Präfix (Vorsilbe) eines längeren Kodewortes sein.
→ Ein Kodewort kann dekodiert werden, sobald das letzte Zeichen empfangen wurde.⁵

Dekodierbarkeit:

Ein Kode ist dekodierbar, wenn aus einer beliebigen Folge von Kodewörtern die ursprünglichen Zeichen der Quelle wiedergewonnen werden können. Maßnahmen dazu sind:

Bei einem Präfixkode ist kein Kodewort Anfang eines anderen Kodewortes.
Bei einem Blockkode hat jedes Kodewort die gleiche Wortlänge.
Bei einem Kommakode wird ein Kommazeichen zur Trennung der Kodewörter verwendet um eine eindeutig Dekodierbarkeit zu erreichen.⁶

Huffman:

Der Huffman-Kode mit variabler Wortlänge liefert bei kleinster mittlere Wortlänge einen optimalen Präfixkode. Er ist ohne Kommazeichen eindeutig dekodierbar.

→ Einsatz in der Bildkodierung (JPEG, MPEG) und Kodierung von digitalen Audio-Signalen.

Gruppen:

Für die Berechnung der Entropie ist die Kenntnis der Wahrscheinlichkeitsverteilung der Symbole notwendig. Man unterscheidet daher bei der Quellenkodierung 3 Gruppen entsprechend den Wahrscheinlichkeiten (Ernst, 2000, Seite 59):

statistische Wahrscheinlichkeiten
Die Symbole werden entsprechend ihrer bekannten (statischen) Wahrscheinlichkeiten unterschiedlich langen Kodewörtern zugeordnet.
→ Huffman-Kodierung, Morse-Kodierung
adaptive Wahrscheinlichkeiten
Die unbekannte Wahrscheinlichkeit der Symbole wird durch eine Häufigkeitsanalyse vor der Kodierung messtechnisch bestimmt.
→ Modifizierte Huffman-Kodierung, Lauflängenkodierung
dynamische Wahrscheinlichkeiten
Die unbekannte Wahrscheinlichkeit der Symbole wird erst während der Kodierung (dynamisch) erstellt.
- Die Lempel- Ziv-Kodierung (LZW, von Lempel, Ziv und Welch) verwendet ein dynamisches Wörterbuch auf Zeichenfolgen an.
- Bei der Arithmetischen Kodierung⁷ wird einem Quellwort eine Gleitpunktzahl zugeordnet.

Beispiel 7.1.1 (Kodierung 1)

Gegeben ist ein Alphabet Q = {a,b,c}. Das Wort „baacbacba“ soll mit dem LZW-Algorithmus kodiert werden, wobei das dynamische Wörterbuch mit a = 1, b = 2 und c = 3 inialisiert ist.

Das rekursive Kodierungsverfahren dazu ist:

Start: Setze i = 0 und w₀ = x₀
Loop: Setze i = i + 1 und w₁ = w₀ + x_i
Ist w₁ im Wörterbuch enthalten?
Ja:

w₀ = w₁
Nein:

Schreibe w₁ in das Wörterbuch

Ausgabe: Index(w₀),

w₀ = x_i
Gehe zu Loop, falls Eingabe nicht zu Ende
Ausgabe: Index(w₀)

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ausgabe:

2, 1,1,3,4,7,1

Beispiel 7.1.2 (Kodierung 2)

Es ist das Wort TESTSTEINE mit Arithmetischer Kodierung zu Kodieren. Die dynamischen Häufigkeiten der Buchstaben für dieses Wort sind:

x_i	T	E	S	I	N

p_abs(x_i)	3	3	2	1	1
p_rel(x_i)	0,3	0,3	0,2	0,1	0,1
Intervall Lo(x_i)	0,0	0,3	0,6	0,8	0,9
Intervall Hi(x_i)	0,3	0,6	0,8	0,9	1,0

Das rekursive Kodierungsverfahren dazu ist:

Start: Setze i = 0, Lo⁽⁰⁾ = 0.0 und Hi⁽⁰⁾ = 1.0
Loop: Setze i = i + 1 und nehme Symbol x_i
- Berechne Interval In⁽ⁱ⁾ = Hi⁽ⁱ⁻¹⁾ − Lo⁽ⁱ⁻¹⁾
- Setze Lo⁽ⁱ⁾ = Lo⁽ⁱ⁻¹⁾ + Lo(x_i) ⋅ In⁽ⁱ⁾
- Setze Hi⁽ⁱ⁾ = Lo⁽ⁱ⁻¹⁾ + Hi(x_i) ⋅ In⁽ⁱ⁾
Gehe zu Loop, falls Symbolwort nicht zu Ende
Kodewort sind alle Zahlen im letzten Intervall

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Zahlenwerte sind:

c(T EST ST EIN E) = 0,147424- ---------

¹Ein Maß für die Optimierung (Güte) ist die im Mittel zu erwartende Länge der Zeichenfolge.

²Mengenlehre: Für jedes x aus X gibt es ein w aus Y _m mit der Eigenschaft c(x) = w.

³Man sieht hier direkt, dass E(c) = 1 ist, wenn die Redundanz R = 0 ist: Einsetzen von L(c)ld(r) = R + H(X) in die Formel der Effizienz.

⁴Quelle: https://www.sttmedia.de/buchstabenhaeufigkeit-deutsch. Kodierung der Buchstaben nach der relativer Häufigkeit in Texten: links für deutsch und rechts für englisch.

⁵Jeder präfixfreie Kode ist eindeutig decodierbar, aber nicht alle eindeutig decodierbaren Kodes sind präfixfrei!

⁶Beispiel Morsekode: Einfache Pause zwischen den Kodebuchstaben und zweifache Pause zwischen den Kodewörtern

⁷Das Verfahren der Arithmetischen Kodierung wird aktuell selten eingesetzt, da es patentrechtlich geschützt ist für die Firmen IBM, AT&T und Mitsubishi

[next] [prev] [prev-tail] [front] [up]