[next] [prev] [prev-tail] [tail] [up]

17.5 Inversion von Ortskurven

Definition:

Die Inversion einer komplexen Größe erfordert die Bildung des Kehrwertes

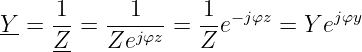1- --1--- 1- −jφz jφy Y- = Z- = Zej φz = Z e = Y e
(17.5.1)

→ Bei bekannter Ortskurve Z ergibt sich die Ortskurve des Kehrwertes Y = 1∕Z durch Inversion der bekannten Ortskurve.

Regeln:

Hilfreiche Konstruktionsregeln sind:

  1. Die Inversion einer Geraden durch den Nullpunkt ergibt wieder eine Gerade durch den Nullpunkt.
  2. Die Inversion eines Kreises nicht durch den Nullpunkt ergibt wieder einen Kreis nicht durch den Nullpunkt.
  3. Die Inversion einer Geraden nicht durch den Nullpunkt ergibt einen Kreis durch den Nullpunkt — und umgekehrt.

In Abb. 17.4.1 aus dem letzten Abschnitt sind zwei inverse Ortskurven entsprechend Regel 3 dargestellt.

Praxis:

Grafische Konstruktion einfacher Ortskurven aufgrund der Berechnung von max. 3 Punkten!

Mathematik:

Die allgemeine Form der parametrisierten Ortskurve hat die Form einer Geradengleichung

G- = A-+ p ⋅ B
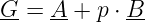(17.5.2)

Der Kehrwert, also die entsprechende Admittanz, bedeutet die Inversion der sogenannten Nennergeraden (G steht im Nenner), die zu einem Kreis durch den Nullpunkt führt

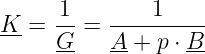1- ----1----- K--= G-= A-+ p ⋅ B
(17.5.3)

Parameter:

Die konjugiert komplexen Zeiger A∗ und B∗ ermöglichen das Zeichnen des Kreises. Die an der reellen Achse gespiegelte Nennergerade

G-∗ = A∗ + p ⋅ B-∗
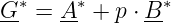(17.5.4)

ermöglicht die Parametrisierung des Kreises.

Graph:

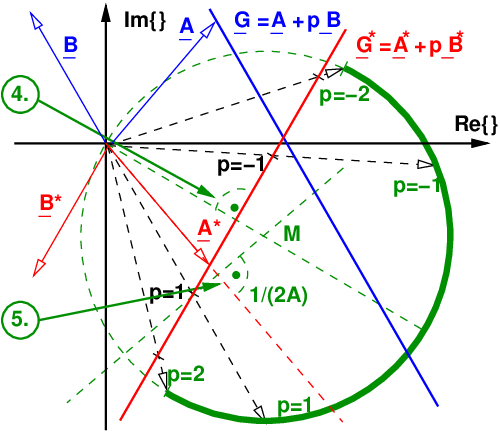
In Abb. 17.5.1 ist die Konstruktion und die Ermittlung der Parameterwerte der Ortskurve eines Kreises durch den Nullpunkt dargestellt.  

PIC

Abbildung 17.5.1: Konstruktion und Ermittlung der Parameterwerte eines Kreises als Ortskurve
Anleitung:

Es empfiehlt sich folgendes schematisierte Vorgehen:

  1. Das Zeichnen der Nennergeraden
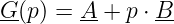
    G-(p) = A-+ p ⋅ B

    wird meistens nicht explizit ausgeführt, da die gespiegelte Nennergerade direkt berechnet werden kann.

  2. Wahl der Achsen für die (an der rellen Achse) gespiegelte Nennergerade
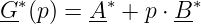
    G∗(p) = A ∗ + p ⋅ B ∗ -- -- --

    für G∗(p min) und G∗(p max) mit gleichem Maßstab für die x- und y-Achse.

  3. Zeichnen der gespiegelten Nennergerade, deren lineare Parameterwerte die Parameter des späteren Kreises sind.
  4. Zeichnen der Senkrechten auf der gespiegelten Nennergeraden G∗, die durch den Nullpunkt läuft.
  5. Berechnen des Abstandes
    -1- AK = |A|

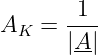
    und Festlegen des Maßstabs für den Kreis, z.B. auf einem analogen Raster zum Maßstab der gespiegelten Nennergeraden.

    Zeichnen der Senkrechten auf A∗ im Abstand A K∕2.

  6. Die Schnittpunkte der beiden Senkrechten ergeben den Mittelpunkt M des Kreises. Zeichnen des Kreises und Markieren des Kreissegmentes entsprechend der gespiegelten Nennergeraden.
  7. Beziffern des Kreises mit den Parameterwerten p entsprechend der gespiegelten Nennergeraden G∗ indem vom Nullpunkt des Koordinatensystems aus Geraden durch die bekannten Parameterwerte der gespiegelten Nennergeraden gezeichnet werden.

Beispiel 17.5.1
(RLC)

Zu einer Reihenschaltung aus R = 25 Ω, L = 80 µH wird ein Kondensator mit CP = 0,5 µF parallelgeschaltet. Die Frequenz ist f = 5 kHz.

  1. Konstruieren Sie die Ortskurve der Admittanz Y = f(L) im Bereich von 0 ⋅ L ≤ L ≤ 50 ⋅ L.
  2. Lesen Sie aus der Ortskurve die beiden Resonanzpunkte der Schaltung ab!
  3. Erklären Sie, warum es zwei Resonanzpunkte gibt!
  4. Berechnen Sie die beiden Resonanz-Induktivitäten der Schaltung und überprüfen Sie die Ergebnisse anhand der Ortskurve!

LÖSUNG:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

  1. Endergebnis der Ortskurve

    PIC

  2. Aus der Ortskurve können die beiden Induktivitäten der Schaltung für Resonanz abgelesen werden, wenn der Parameter hinreichend fein eingezeichnet wird:
    L1 = 5 ⋅ 80µH = 0,4mH L2 = 20 ⋅ 80µH = 1,6mH
  3. Nullsetzen des Imaginärteils ergibt die Zahlenwerten
    L1 = 0,3860-⋅ 10−-3H ----------−-3-- L2 = 1,6404-⋅ 10--H-

[next] [prev] [prev-tail] [front] [up]