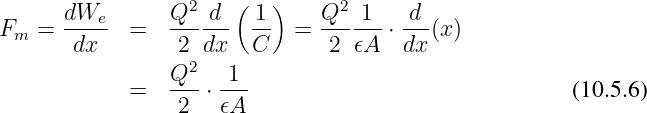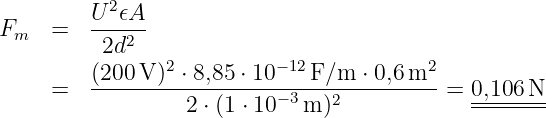Kräfte im elektrischen Feld

10.5 Kräfte im elektrischen Feld

Kondensator:

Aufgrund des Coulombschen Gesetzes ziehen sich die unterschiedlich geladenen Platten eines Kondensators an.

→ Es ist dabei zu beachten, dass es sich hierbei um Ladungen auf einer Fläche und nicht um Punktladungen handelt!

Abbildung 10.5.1: Herleitung der Kraft auf die Platten beim Kondensator

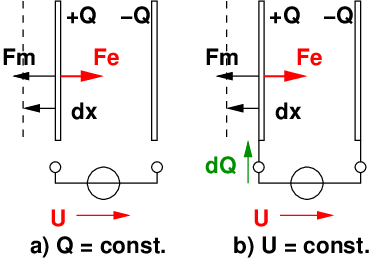
Zur Herleitungen der Kraft könnten wir die Fälle mit konstanter Ladung Q oder konstanter Spannung U unterscheiden, wie in Abb. 10.5.1 dargestellt .

Kräfte:

Wird eine Ladung Q gegen die elektrische Feldkraft F_e verschoben, so muss dafür die mechanische Kraft F_m aufgewendet werden

F⃗m = F⃗e

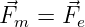(10.5.1)

Energie:

Die Berechnung dieser Kräfte ist aus dem Energieerhaltungssatz möglich. Bei einer kleinen Verschiebung³³ einer Platte um den Weg dx mit der Kraft F_m wird die mechanische Energie

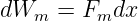dWm = Fmdx

(10.5.2)

als Änderung der elektrischen Energie dem Kondensator zugeführt

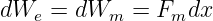dWe = dWm = Fmdx

(10.5.3)

Kraft:

Auflösen nach der mechanischen Kraft zum Verschieben einer Platte liefert die allgemeine Beziehung

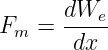dWe-- Fm = dx

(10.5.4)

Q = const.

Diese Herleitung ist nur richtig, wenn sich die Energie der Spannungsquelle nicht ändert. Dann können wir für die Änderung der elektrischen Energie auf dem Kondensator schreiben

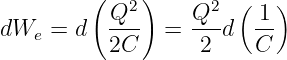( ) ( ) Q2- Q2- 1- dWe = d 2C = 2 d C

(10.5.5)

und für die mechanische Kraft auf die Platten

dW Q2 d ( 1) Q2 1 d Fm = ----e = ------ -- = ------⋅ ---(x ) dx 2 dx C 2 ϵA dx Q2- -1- = 2 ⋅ϵA (10.5.6)

U = const.

Die Änderung der elektrischen Energie auf dem Kondensator ist proportinal zur Änderung der Kapazität

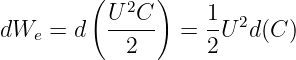( 2 ) dWe = d U-C-- = 1U 2d(C ) 2 2

(10.5.7)

Dabei nimmt die Energie der Spannungsquelle bei konstanter Spannung³⁴ zu

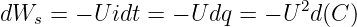2 dWs = − U idt = − U dq = − U d(C )

(10.5.8)

Ergebnis:

Die mechanische Kraft auf die Platten wird jetzt zu

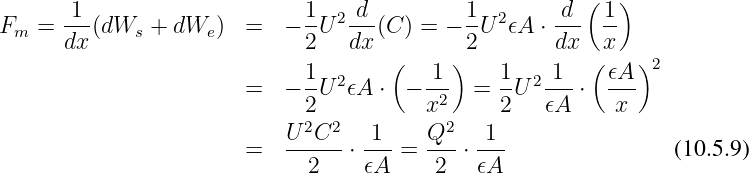
( ) F = 1-(dW + dW ) = − 1U 2-d-(C ) = − 1U 2ϵA ⋅ d-- 1- m dx s e 2 dx 2 dx x 1 ( 1 ) 1 1 ( ϵA )2 = − -U 2ϵA ⋅ − --2 = --U 2---⋅ --- 2 x 2 ϵA x U-2C2- -1- Q2- -1- = 2 ⋅ϵA = 2 ⋅ϵA (10.5.9)

Die Kraft auf die Platten ist unabhängig von dem Anschluss an der Spannungsquelle, da Sie von den Ladungen auf den Platten ausgeht. Mit Q = DA erhalten wir die Kraft zu

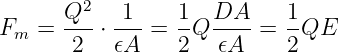2 F = Q-- ⋅-1- = 1-Q DA--= 1QE m 2 ϵA 2 ϵA 2

(10.5.10)

Punkt:

Bei der Definition der Feldstärke einer Punktladung mit Gln. 10.2.1 hatten wir die fast identische Beziehung

Fe = QE

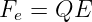
Der Unterschied zum Feld einer Punktladung kommt vom Feld einer Linien- bzw. Flächenladung auf dem Kondensator.

Platte:

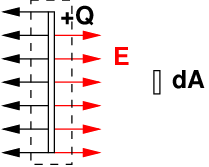
Nehmen wir das elektrische Feld einer Platte und betrachten wir deren Wirkung auf ein sehr kleines Flächenelement der anderen Platte entsprechend Abb. 10.5.2.

Abbildung 10.5.2: Elektrisches Feld einer Kondensator-Platte durch Superposition

Kraft:

Das elektrische Feld dieser Ladung haben wir bereits im Kondensator als homogenes Feld durch durch Superposition kennengelernt. Jetzt kann Gln. 10.2.1 angewendet werden auf die Ladung ΔQ auf der Platte ΔA

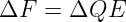ΔF = ΔQE

(10.5.11)

Ergebnis:

Umgeben wir die Platte mit der Fläche A mit einem Quader so fließen die Feldlinien im wesentlichen nur durch die Vorder- und die Rückseite des Quaders jeweils durch eine Fläche der Größe A, insgesamt also 2A. Damit erhalten wir

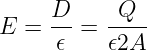D Q E = -- = ---- ϵ ϵ2A

(10.5.12)

Einsetzen ergibt die Kraft der Flächenladung auf ein kleines Flächenelement (der anderen Platte) zu

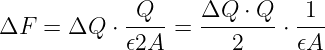ΔF = ΔQ ⋅-Q--= ΔQ--⋅ Q-⋅-1- ϵ2A 2 ϵA

(10.5.13)

Addieren wir über die Fläche der zweiten Platte auf, so erhalten wir die Kraft zwischen den zwei Platten eines Kondensators ebenfalls zu

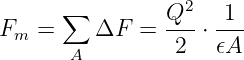∑ Q2 1 Fm = ΔF = ---⋅--- A 2 ϵA

(10.5.14)

Beispiel 10.5.1 (Kondensator)

Wie groß ist die Kraft, mit der sich die beiden Elektroden eines Plattenkondensators mit der Fläche A = 0,6 m², dem Abstand d = 1 mm und Luft als Dielektrikum (ϵ_r = 1) anziehen, wenn der Kondensator auf die Spannung U = 200 V aufgeladen ist?

Hinweis:

Überlegen Sie, welche Größen der elektrischen Energie sich als Funktion des Weges ändern und welche konstant bleiben.

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Kraft

U 2ϵA Fm = ---2-- 2d 2 −12 2 = (200-V)--⋅ 8,85 ⋅ 10-F∕m--⋅ 0,6m--= 0,106 N 2 ⋅ (1 ⋅ 10−3m )2 --------

³³Prinzip der virtuellen Verschiebung: Eigentlich bleibt alles wie es ist und man fragt sich nur, wie würde es sich ändern, wenn …

³⁴negativ, da aufgenommene Energie

[next] [prev] [prev-tail] [front] [up]