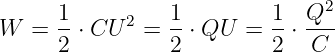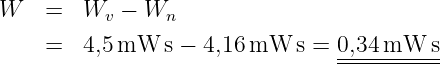10.4 Energie im elektrischen Feld

Strom:

Mit Gln. 10.3.9 haben wir die gespeicherte Energie berechnet, die dem Kondensator beim Ladevorgang zugeführt wird

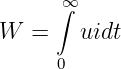(10.4.1)

Ladung:

Die Stromänderung ist gleich dem Ladungszuwachs

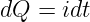(10.4.2)

so dass wir beim (Platten-) Kondensator mit der Spannung

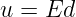(10.4.3)

und der Ladung

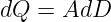(10.4.4)

die elektrische Energie ohne genaue Kenntnis des Strom- und Spannungsverlaufs aus den Feldgrößen berechnen können

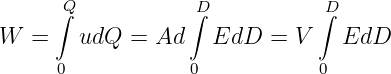(10.4.5)

mit dem vom Feld durchsetzen Volumen V des Kondensators.

Dichte:

Die in einem Kondensator gespeicherte Energie ist nicht auf den Elektroden gespeichert, sondern im elektrischen Feld, also im Dielektrikum. Mit der Energiedichte wird dazu eine Größe in jedem Raumpunkt definiert

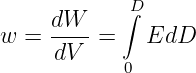(10.4.6)

→ Für konstantes ϵ erhalten wir mit D = ϵE für die Energiedichte

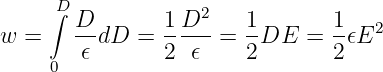(10.4.7)

→ Diese für den Plattenkondensator hergeleitete Beziehung gilt ganz allgemein auch in inhomogenen Feldern, da man einen beliebigen Kondensator aus der Zusammenschaltung von entsprechenden Elementar-Plattenkondensatoren realisieren kann.

Beispiel 10.4.1
(Energieverlust)

Wie groß ist der Energieverlust, wenn die Kondensatoren C₁ = 10 µF mit der Ladung Q₁ = 0,1 mC und C₂ = 20 µF mit der Ladung Q₂ = 0,4 mC parallel geschaltet werden?
Hinweis:
Überlegen Sie, warum Sie welche Form der Gln. 10.3.9

verwenden müssen?

Was besagt der Energieerhaltungssatz?

Was bedeutet Energieverlust in einem abgeschlossenem System?

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Energieverlust