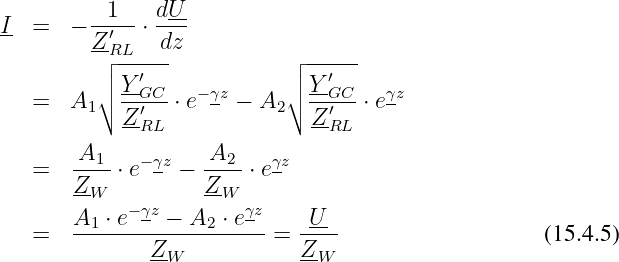Lösung der Telegraphengleichung

Ansatz:

Durch Einsetzen des Exponentialansatz

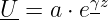U- = a ⋅ eγz

(15.4.1)

in die DGL 15.3.11 erhalten wir die Fortpflanzungskonstante zu

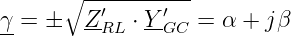∘--′-----′-- γ-= ± Z-RL ⋅ Y-GC = α + jβ

(15.4.2)

Lösung:

Da sich zwei Lösungen ergeben ist die Lösung allgemein für die Spannung

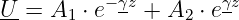−γz γz U-= A1 ⋅ e- + A2 ⋅ e

(15.4.3)

mit den Konstanten A₁ und A₂ bzw.

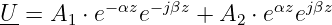−αz −jβz αz jβz U- = A1 ⋅ e e + A2 ⋅ e e

(15.4.4)

mit der Dämpfungskonstanten bzw. dem Dämpfungsbelag α und der Phasenkonstanten (bzw. dem Phasenbelag) β.

Strom:

Die allgemeine Lösung für den Strom erhalten wir aus der Spannungsgleichung 15.3.7 durch Einsetzen der 1. Ableitung der Spannung zu

1 dU- I- = − -′---⋅--- Z┌RL---dz ┌ ----- ││ Y′ ││ Y′ = A1∘ -G′C--⋅ e−γz − A2∘ -G′C--⋅ eγz ZRL ZRL A1 − γz A2 γz = ----⋅ e - − ----⋅ e ZW −γz ZW γz A1-⋅ e---−-A2-⋅ e-- -U-- = ZW = ZW (15.4.5)

mit dem Wellenwiderstand

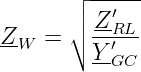┌│ --′-- Z- = │∘ -ZRL- W Y-′GC

(15.4.6)

Zeit:

Aus den komplexen Zeigern erhalten wir die Zeitabhängigkeit, wenn wir den komplexen Drehfaktor e^jωt wieder einführen. Für die Spannung ergibt sich

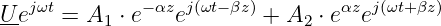jωt −αz j(ωt−βz) αz j(ωt+βz) U-e = A1 ⋅ e e + A2 ⋅ e e

(15.4.7)

Der erste Ausdruck rechts stellt eine Welle dar, die sich in positiver z-Richtung ausbreitet. Der Faktor

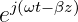j(ωt−βz) e

(15.4.8)

ist konstant für

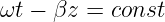ωt − βz = const

(15.4.9)

das eine Ausbreitungsgeschwindigkeit gleicher Punkte bedeutet mit

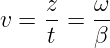z ω v = --= -- t β

(15.4.10)

in zunehmender x-Richtung entlang der Leitung, wobei die Amplitude exponentiell abnimmt.

Echo:

Der zweite Ausdruck stellt entsprechend eine vom Ende der Leitung zum Anfang zurück laufende Welle — der sogenannten Echowelle — dar.

Wellen:

Aus der Spannung U_h₀ am Leitungsanfang ergibt sich entsprechend Gln 15.4.3 die Spannung der Hauptwelle zu

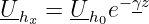U-hx = U-h0e− γz

(15.4.11)

und mit Gln 15.4.5 der Strom der Hauptwelle zu

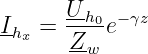I- = Uh0e− γz hx Zw

(15.4.12)

und mit der Spannung U_r₀ ergibt entsprechend die Spannung der Echowelle zu

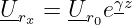U-rx = Ur0eγz

(15.4.13)

und der Strom der Echowelle⁴ zu

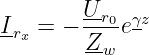U-r γz Irx = − ---0e- Zw

(15.4.14)

⁴Der Echostrom ist negativ, da er entgegen dem Hauptstrom fließt.