Telegraphengleichung

15.3 Telegraphengleichung

Modell:

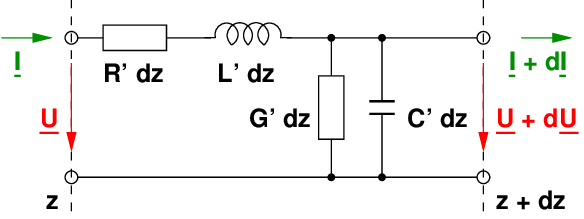
Die Energien des elektrischen und magnetischen Feldes werden durch verteilte Kondensatoren und Spulen und die Verluste in den Leitungen durch verteilte Widerstände und Leitwerte modelliert.

Frequenz:

Hinsichtlich der Frequenz sind die „Leitungskonstanten“ jedoch nicht konstant:

Der Kapazitätsbelag nimmt nur wenig mit steigenden Frequenzen ab
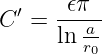
$′ ϵπ C = ln--a- r0$ (15.3.1)
Bei hohen Frequenzen verschwindet der Summand 1∕4 beim Induktivitätsbelag
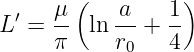
$( ) ′ μ- a- 1- L = π ln r + 4 0$ (15.3.2)
Aufgrund des Skineffektes wächst der Widerstandsbelag mit steigender Frequenz.
Der Ableitungsbelag steigt bei höheren Frequenzen proportional zur Frequenz an aufgrund der dielektrischen Verluste.

ESB:

Bei homogenen Leitungen kann für ein kurzes Leitungsstück mit diskreten Bauelementen das vereinfachte Ersatzschaltbild in Abb. 15.3.1 verwendet werden.

Abbildung 15.3.1: ESB zur Telegraphengleichung

Messung:

Aus einer Kurzschlussmessung mit dem Widerstand Z_K ergeben sich der Widerstands- und Induktivitätsbelag zu

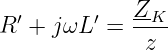Z- R ′ + jωL ′ =--K- z

(15.3.3)

Aus einer Leerlaufmessung mit dem Widerstand Z_L ergeben sich der Ableitungs- und Kapazitätsbelag zu

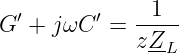G′ + jωC ′ = -1--- zZL

(15.3.4)

Spannung:

Mit dem komplexen Längswiderstand

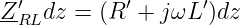Z-′ dz = (R ′ + jωL ′)dz RL

(15.3.5)

erhalten wir die Maschengleichung

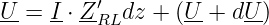′ U- = I-⋅ Z-RLdz + (U-+ dU)

(15.3.6)

bzw. durch Umstellen

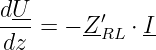dU- = − Z-′RL ⋅ I dz

(15.3.7)

Strom:

Mit dem komplexen Querleitwert

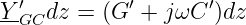Y′GC dz = (G ′ + jωC ′)dz

(15.3.8)

erhalten wir die Knotengleichung

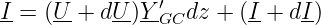I-= (U-+ dU)Y-′GC dz + (I + dI)

(15.3.9)

bzw. durch Umstellen

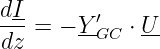dI-= − Y-′ ⋅ U dz GC

(15.3.10)

unter der Voraussetzung dU ≪ U.

DGL:

Wenn man die Spannungsgleichung 15.3.7 nach dz differenziert kann man die Stromgleichung 15.3.10 einsetzen und erhält aus dem System gekoppelter DGLs erster Ordnung die lineare DGL zweiter Ordnung

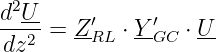d2U- ′ ′ ---2 = Z-RL ⋅ Y-GC ⋅ U dz

(15.3.11)

[next] [prev] [prev-tail] [front] [up]