Für eine kontinuierliche Leitung mit
- Widerstandsbelag mit [R′] = Ω∕m,
- Induktivitätsbelag mit [L′] = H∕m,
- Kapazitätsbelag mit [C′] = F∕m und
- Ableitungsbelag mit [G′] = S∕m
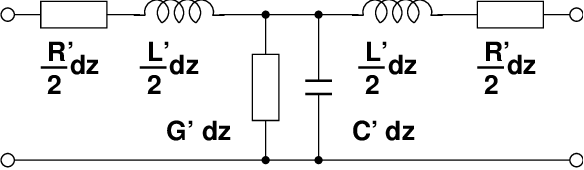
stellen wir ein Modell mit diskreten Bauelementen für kurze Leitungen der Länge dz, wie in Abb. 15.2.1 dargestellt, auf.
Bei homogenen Leitungen sind die geometrischen Abmessungen und die Materialeigenschaften über die gesamte Länge konstant.
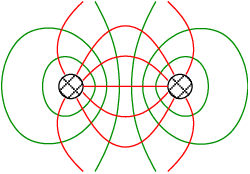
Für eine Parallelleitung erhalten wir wie in Abb. 15.2.2 dargestellt elektromagnetische Feldlinien, die senkrecht zur Ausbreitungsrichtung der elektromagnetischen Transversalwelle (TEM) sind.
→ Diese homogenen Leitungen werden auch Lecher-Leitung3 genannt.
Auf am Ende leerlaufenden oder kurzgeschlossenen Lecherleitungen bilden sich stehende Wellen mit der Freuqenz der Anregung aus:
- Zur Anpassung oder zur Bestimmung einer unbekannten Wellenlänge (bzw. der Frequenz) befindet sich auf der Leitung u.U ein Kurzschlussschieber.
- Die verteilte Kapazität und Induktivität der Leitung bildet einen Schwingkreis, der als Bandpass oder Bandsperre verwendet werden kann.
- Eine offene Leitung mit Vielfachen von λ∕4 der Wellenlänge ergibt einen Reihenschwingkreis.
- Eine kurzgeschlossen Leitung mit Vielfachen von λ∕4 der Wellenlänge hat einen unendlichen Eingangswiderstand.
→ Anwendungen in der HF-Technik bei koaxialen oder Streifenleitern.
Aus der Anwendung der Kirchhoffschen Maschen- und Knotengleichungen ergibt sich eine Differentialgleichung mit konstanten Koeffizienten zweiter Ordnung, die (aufgrund der impliziten Zeitabhängigkeit der komplexen Größen) auch als Wellengleichung bezeichnet wird.
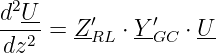 | (15.2.1) |
Die Lösung dieses Systems ergibt sich bei einer harmonischen Anregung zu
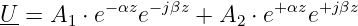 | (15.2.2) |
mit den Eigenschaften