[next] [prev] [prev-tail] [tail] [up]

15.1 Maxwellsche Gleichungen

System:

Die Beziehungen zur Beschreibung der Wechselwirkungen zwischen zeitlich veränderlichen elektrischen und magnetischen Feldern werden als

System der Maxwellschen Gleichungen2

bezeichnet.

1. M-Gln.:

Das verallgemeinerte Durchflutungsgesetz besagt, dass die Wirbel des magnetischen Feldes an jeder Stelle gleich der wahren Stromdichte an dieser Stelle sind

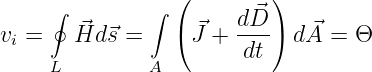∮ ∫ ( ) v = ⃗Hd ⃗s = ( ⃗J + dD⃗-) d⃗A = Θ i dt L A
(15.1.1)

2. M-Gln.:

Das Induktionsgesetz besagt, dass die induzierte Quellenspannung entlang eines beliebigen geschlossenen Weges gleich der Flussänderung ist

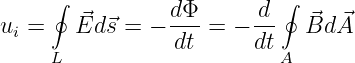∮ ∮ ui = ⃗Ed ⃗s = − dΦ-= − d- ⃗Bd ⃗A dt dt L A
(15.1.2)

3. M-Gln.:

Das magnetische Feld ist ein Wirbelfeld bei dem die geschlossenen B-Feldlinien die sie erregende elektrische Durchflutung umgeben. Es gibt keine magnetischen Quellen

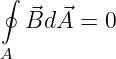∮ B⃗d A⃗ = 0 A
(15.1.3)

4. M-Gln.:

Das wirbelfreie elektrische Strömungsfeld enthält D-Feldlinien, die auf positiven Ladungen beginnen und auf negativen enden. Die Quellen und Senken dieses Quellenfeldes sind also die positiven und negativen Ladungen

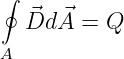∮ ⃗Dd ⃗A = Q A
(15.1.4)

→ Zu beachten ist, das dass induzierte elektrische Feld entsprechend der 2. Maxwellschen Gleichung wie das magnetische Feld ein Wirbelfeld ist mit geschlossenen elektrischen Feldlinien.

5.-7. M-Gln.:

Der Zusammenhang zwischen den Feldvektoren wird mit den Materialgleichungen beschrieben. Es ergibt sich das elektrische Strömungsfeld

⃗J = γE⃗
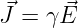(15.1.5)

und das dielektrische Verschiebungsfeld

E⃗ = 1-⃗D ϵ
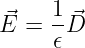(15.1.6)

und das magnetische Feld

B⃗ = μH⃗
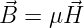(15.1.7)

Knotenregel:

Aus der 1. Maxwellschen Gleichung 15.1.1 ergibt sich als Spezialfall der Integration über eine geschlossene Hüllfläche der austretende Strom

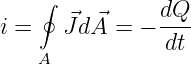∮ dQ i = J⃗d⃗A = − -dt A
(15.1.8)

als Ladungsabnahme in dem eingeschlossenen Gebiet.

Gleichstrom:

In Gleichstromnetzen ist in einem idealen Knoten keine Ladung gespeichert. Somit wird

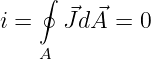∮ i = J⃗d⃗A = 0 A
(15.1.9)

Konzentrieren wir den Strom auf N Leiter, die in den Knoten hineingehen, so erhalten wir die Kirchhoffsche Knotenregel entsprechend zu

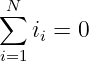N ∑ i = 0 i=1 i
(15.1.10)

Wechselstrom:

Bei Wechselstromnetzen ist eine zeitliche Zu- oder Abnahme der Ladungen möglich. Die Kirchhoffsche Knotenregel gilt analog nur bei Netzwerken mit konzentrierten Bauelementen und widerstandslosen Leitungen zu den Knotenpunkten. Dann gilt aber entsprechend

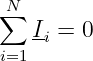∑N Ii = 0 i=1
(15.1.11)

Maschenregel:

Mit der 2. Maxwellschen Gleichung 15.1.2 ergibt die Integration der elektrischen Feldstärke entlang eines geschlossenen Weges die Induktionsspannung

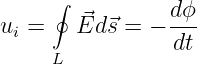∮ ui = ⃗Ed ⃗s = − dϕ- dt L
(15.1.12)

die bei einem Rechte-Hand-Koordinatensystem der Zählpfeile gleich der zeitlichen Abnahme des magnetischen Flusses ist.

Gleichstrom:

Da in Gleichstromnetzen alle magnetischen Flüsse zeitlich konstant sind wird

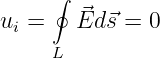∮ u = ⃗Ed ⃗s = 0 i L
(15.1.13)

Verteilen wir die Spannung auf N Bauteile entlang des Weges, so erhalten wir die Kirchhoffsche Maschenregel zu

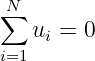N ∑ u = 0 i=1 i
(15.1.14)

Wechselstrom:

Da bei Wechselstromnetzen zeitveränderliche Ströme zu einem zeitveränderlichen Fluss führen ist i.a. ui≠0. Nur bei Netzwerken mit konzentrierten Bauelementen und widerstandslosen Leitungen ohne magnetische Wirkung des Stromes gilt entsprechend

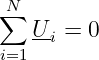N∑ U-i = 0 i=1
(15.1.15)

2Zu Ehren von James Clark Maxwell, 1738 – 1879, britischer Physiker

[next] [prev] [prev-tail] [front] [up]