14.1 Gegeninduktivität

 

---

Zwei räumlich benachbarte stromdurchflossene Leiterschleifen beeinflussen sich gegenseitig über die mit ihnen verknüpften magnetischen Felder.

Abbildung 14.1.1: Zwei magnetisch gekoppelte Leiterschleifen

---

Induktion:

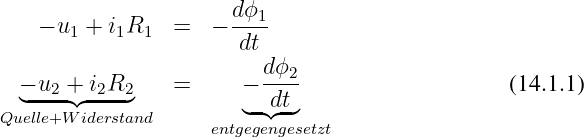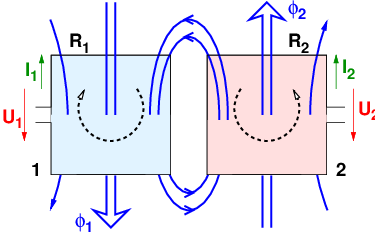
In den beiden Leiterschleifen in Abb. 14.1.1 werden Spannungen entsprechend dem Induktionsgesetz induziert. Unter Berücksichtigung der Leitungswiderstände erhalten wir

Induktivität:

Mit der Selbstinduktivität L einer Leiterschleife ist der Zusammenhang zwischen Spannung und Strom gegeben zu

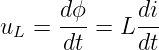
Daraus erhalten wir direkt den linearen Zusammenhang

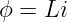(14.1.2)

Teilflüsse:

Die Flüsse ϕ₁ und ϕ₂ werden von beiden Strömen verursacht. Der Beitrag des Stromes i₁ zum Fluss in Schleife 1 ist

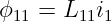(14.1.3)

und der Beitrag des Stromes i₂ zum Fluss in derselben Schleife ist

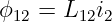(14.1.4)

Summe:

Der Gesamtfluss in Schleife 1 ist dann

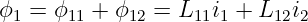(14.1.5)

Entsprechend ergibt sich der Gesamtfluss in Schleife 2 zu

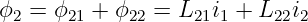(14.1.6)

Selbst:

Die Proportionalitätskonstanten L₁₁ und L₂₂ sind die Selbstinduktivitäten der Schleifen 1 und 2, für die vereinfachend geschrieben wird

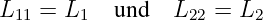(14.1.7)

Gegen:

Die Größen L₁₂ und L₂₁ werden als Gegeninduktivitäten zwischen den Schleifen 1 und 2 bezeichnet. Da der Einfluss von Schleife 1 auf 2 gleich dem von Schleife 2 auf 1 ist gilt

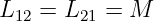(14.1.8)

Setzt man die Ergebnisse in das Gleichungspaar 14.1.1 ein, so erhält man folgende 2 Maschengleichungen als Ergebnis
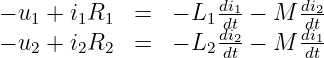