Magnetische Flussdichte und Feldstärke

12.2 Magnetische Flussdichte und Feldstärke

Flussdichte:

Die magnetische Flussdichte B ist definiert durch die Kraft F , die auf eine bewegte Ladung Q im Magnetfeld ausgeübt wird.

→ Sind Q, v und F_m bekannt, so kann mit Gln. 12.1.5 die magnetische Flussdichte B bestimmt werden. In Analogie dazu wurde entsprechend die elektrische Feldstärke über die Kraft F_e = QE auf ruhende Ladungen definiert.

Einheit:

Die Einheit der Flussdichte ist das Tesla¹⁰

[B ] = T = V-s m2

(12.2.1)

Eigenschaften:

Die Feldlinien von B verlaufen tangential im Uhrzeigersinn um bewegte positive Ladungen. Sie sind in sich geschlossen, d.h. B ist quellenfrei. Es gibt keine magnetische Ladung¹¹.

→ Mathematisch beschreibt der Gaußsche Satz die Quellenfreiheit des Magnetfeldes¹²

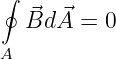∮ B⃗d A⃗ = 0 A

(12.2.2)

Raum:

Die magnetische Flussdichte nach Gln. 12.1.3 schließt über die magnetische Permeabilität

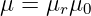μ = μr μ0

(12.2.3)

mit der magnetischen Feldkonstanten

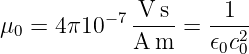μ0 = 4π10− 7-V-s = -1-- A m ϵ0c20

(12.2.4)

die magnetischen Eigenschaften des Raumes (Vakuum μ_r = 1) mit ein. c₀ = 3 ⋅ 10⁸m∕s ist dabei die Lichtgeschwindigkeit im Vakuum.

Feldstärke:

Durch Division der Flussdichte durch die Materiegröße erhalten wir die Definition der magnetischen Feldstärke¹³.

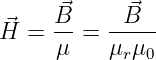⃗ ⃗B- --⃗B-- H = μ = μr μ0

(12.2.5)

mit der Einheit

[B ] V s∕m2 A [H ] = ----= ---------- = -- [μ0] V s∕ (A m ) m

(12.2.6)

Beispiele:

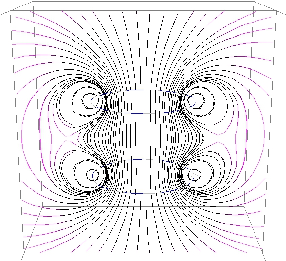
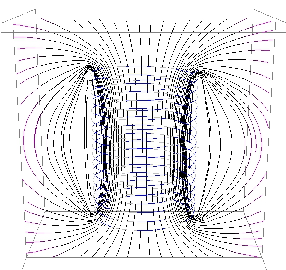
Die magnetischen Feldbilder einer Doppelschleife und einer Spule, wie in Abb. 12.2.1 zu sehen, können mit einem Java-Applet¹⁴ erzeugt werden.

Abbildung 12.2.1: Magnetische Feldbilder einer Doppelschleife (links) und einer Spule (rechts)

¹⁰Zu Ehren von Nicola Tesla, 1856 – 1953, kroatischer Physiker, dessen Teslatransformator hochfrequente Wechselströme hoher Spannung für die Medizintechnik erzeugt.

¹¹Bemerkung: Sowohl B als auch D sind stetig in verschiedenen Materialien, d.h. es existieren keine Sprünge an Grenzen verschiedener Materialien.

¹²Quellen des elektrischen Feldes Ψ = ∮ _ADdA = Q. Gibt es beim Dauermagneten separierbare Pole? Was passiert beim Brechen eines Dauermagneten?

¹³Bemerkung: Sowohl H als auch E sind materialabhängig, d.h. es existieren Sprünge an Grenzen verschiedener Materialien.

¹⁴http://www.falstad.com

[next] [prev] [prev-tail] [front] [up]