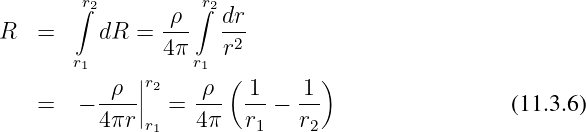Bestimmung von Leitwerten

11.3 Bestimmung von Leitwerten

Leitwert:

Kommen wir zurück zur Berechnung eines Leitwertes aus der Feldverteilung.

Homogen:

Bei homogenen Feldern können wir aus der Stromdichte direkt den Strom

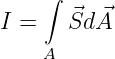∫ I = S⃗d A⃗ A

(11.3.1)

und aus dem elektrischen Feld

⃗ ⃗S- E = κ

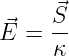(11.3.2)

durch Integration die Spannung

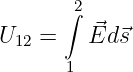∫2 ⃗ U12 = Ed ⃗s 1

(11.3.3)

bestimmen. Daraus ergibt sich die Formel zur Berechnung eines Leitwertes aus symmetrischen Feldgrößen zu¹

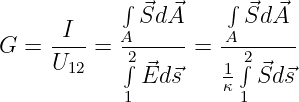∫S⃗d A⃗ ∫ ⃗SdA⃗ -I-- A------ -A------ G = U = 2∫ = 2∫ 12 ⃗Ed ⃗s 1κ ⃗Sd⃗s 1 1

(11.3.4)

Inhomogen:

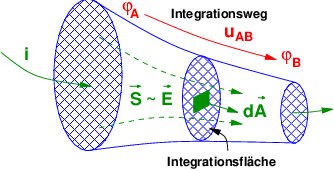
Die Integrationen sind an die Feldverhältnisse anzupassen wie in Abb. 11.3.1 zu sehen ist . Die Leitwertberechnung ist daher nur für symmetrische Felder geschlossen durchführbar.

Abbildung 11.3.1: Integrationsweg und -fläche in inhomogenen Feldern

→ Bei inhomogenen Feldern kann eine Zerlegung des Feldraumes in differentielle Raumelemente erfolgen, in denen näherungsweise homogene Feldverhältnisse bestehen.

→ Anschließend erfolgt eine Reihen-Parallelschaltung aller Teilleitwerte.

→ numerische Berechnung mit der Finite-Elemente-Methode

Radial:

Als Sonderfall inhomogener Felder können radialsymmetrische Felder einfach behandelt werden — wenn das dazu passende Koordinatensystem verwendet wird, wie in Abb. 11.3.1 zu sehen ist .

Abbildung 11.3.2: Integrationsweg und -fläche bei radialsymmetrischen Feldern

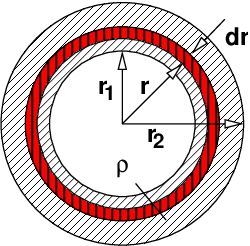
→ Der Raum zwischen den Kugeln besteht aus einzelnen Hohlkugeln mit der Oberfläche A = 4πr² und der Dicke dr.

Widerstand:

Aus dem Widerstand einer einzelnen Hohlkugel

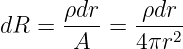ρdr ρdr dR = ----= ---2- A 4πr

(11.3.5)

ergibt sich der Gesamtwiderstand zwischen den beiden Kugeln durch Integration zu

r r ∫ 2 ρ ∫2dr R = dR = --- --2 r1 4π r1 r ρ ||r2 ρ ( 1 1 ) = − ---|| = --- --− -- (11.3.6) 4πr r1 4π r1 r2

→ Der Leitwert ist der Kehrwert des Ergebnisses.

→ Analoge Berechnungen können bei Metallzylindern mit der Oberfläche A = 2πrl angestellt werden und führen zum Ergebnis.

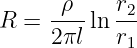-ρ-- r2 R = 2πl ln r 1

(11.3.7)

Beispiel 11.3.1 (Leiter)

In Leitern (Metallen) ist die Geschwindigkeit der Ladungsträger linear proportional zur elektrischen Feldstärke aufgrund der Reibung (Stoßvorgänge mit Gitterbausteinen). Bezeichnen wir die Proportionalität mit μ so erhalten wir eine mittlere Geschwindigkeit der Elektronen von v_n = −μ_nE.

Wie groß ist die Geschwindigkeit der Elektronen in einer Kupferleitung mit einer Konzentration der Elektronen von n = 8,6 ⋅ 1022∕cm³, einem spezifischen Leitwert κ = 56,180 S m∕mm² bei einer typischen Stromdichte S = 10 A∕mm² für Haushaltsleitungen?

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Elektronengeschwindigkeit

2 − 3 vn = μnE = 40,8cm ∕V s ⋅ 1,78 ⋅ 10 V∕cm = 0,0726cm-∕s-

¹Vergleiche Gln. 10.3.10 beim Kondensator für C = Q∕u

[next] [prev] [prev-tail] [front] [up]