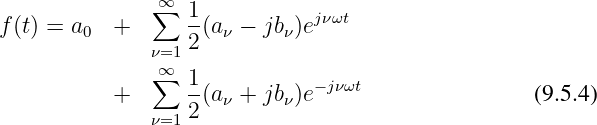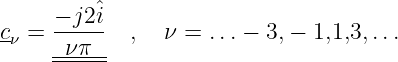Die komplexe Fourierreihe ist die mathematische Grundlage der Einführung der Fourier- und Laplace-Transformationen!
Mit Hilfe der Euler-Gleichungen (Papula, 2006, Seite 221)
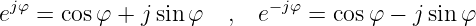 | (9.5.1) |
ergibt sich für die Kosinus- und die Sinusfunktion durch Addition bzw. Subtraktion
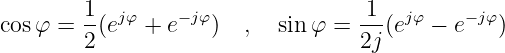 | (9.5.2) |
Setzt man diese Ergebnisse in die Fourierreihe nach Gln. 9.3.10 ein und lässt die Anzahl n →∞ gehen, so ergibt sich
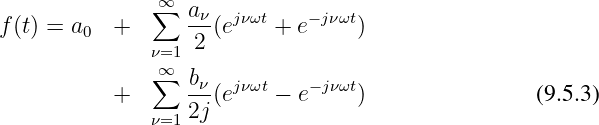
und entsprechendes Zusammenfassen wird daraus5
Die komplexen Koeffizienten lassen sich mit den Fourierkoeffizienten nach Gln. 9.4.13 und 9.4.14 darstellen als
![c = 1( a − j b )
-ν 2 ◟◝ν◜◞ ◟◝ν◜◞
9.4.13 9.4.14
1 to∫+T
= -- f(t)[cos(νωt) − j sin(νωt )]dt
T t0 ◟---------◝◜---------◞
t +T mit Gln.9.5.1
1 o∫ −jνωt
= -- f(t)e dt (9.5.5)
T t0](gde_2282x.png)
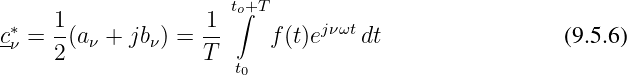
Für den Index ν = 0 ergibt sich für beide komplexen Koeffizienten
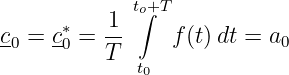 | (9.5.7) |
was entsprechend Gln. 9.4.12 dem Gleichanteil entspricht.
Aus den Definitionsgleichungen der komplexen Koeffizienten ist zu
sehen, dass cν∗ = 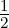 (aν + jbν) zu cν =
(aν + jbν) zu cν = 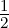 (aν − jbν) wird, wenn die
Laufvariable ν durch −ν ersetzt wird.
(aν − jbν) wird, wenn die
Laufvariable ν durch −ν ersetzt wird.
Damit lassen sich die drei Terme der Gln. 9.5.4 zur komplexen Fourierreihe zusammenfassen
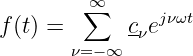 | (9.5.8) |
mit den komplexen Koeffizienten
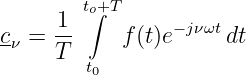 | (9.5.9) |