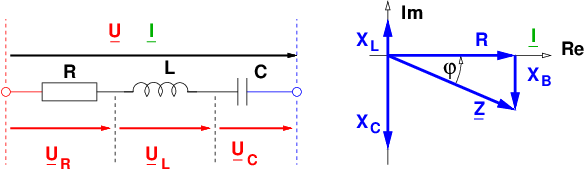
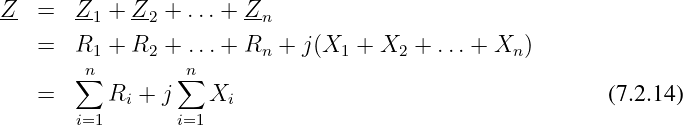Impedanz

Impedanz:

Der allgemeine komplexe Widerstand (Impedanz) enthält reale (Resistanz) und imaginäre (Reaktanz) Anteile von Wirkwiderstand, Spule und Kondensator.

Abbildung 7.2.1: Widerstand, Spule und Kondensator in Reihe: Schaltbild und Zeigerdiagramm für Widerstände

Zeiger:

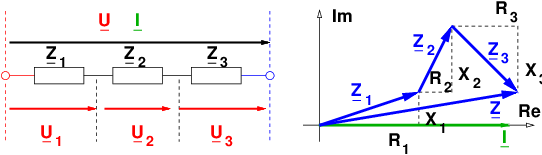
Wir erhalten damit für eine Reihenschaltung der 3 idealen Zweipole nach Abb. 7.2.1

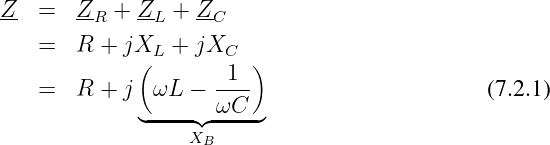
Z- = ZR + ZL + ZC = R + jXL( + jXC ) = R + j ωL − -1-- (7.2.1) ----- ωC--- ◟ ◝X◜ ◞ B

Betrag:

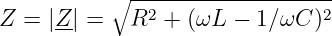∘ -------------------- Z = |Z| = R2 + (ωL − 1∕ωC )2

(7.2.2)

Phasenwinkel:

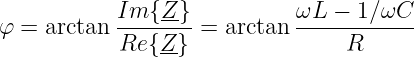φ = arctan Im-{Z-}-= arctan ωL-−--1∕ωC-- Re {Z} R

(7.2.3)

Reeller Widerstand:

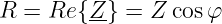R = Re {Z } = Z cos φ --

(7.2.4)

Imaginärer Blindwiderstand:

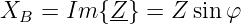XB = Im {Z-} = Z sinφ

(7.2.5)

Bemerkung:

Da die beiden Blindwiderstände X_L und X_C verschiedene Vorzeichen haben, unterscheidet man:

X_B < 0:

Kapazitive Impedanz → negativer Phasenwinkel

X_B = 0:

Resonanz: Nur Wirkwiderstand → Phasenwinkel ist Null

→ Anwendung: Schwingkreise, Bandfilter und -sperren

X_B > 0:

Induktive Impedanz → positiver Phasenwinkel

Schaltbild:

Durch die RLC-Reihenschaltung fließt derselbe Strom:

→ Als Bezugszeiger wird der Strom I gewählt.

Teilspannungen:

Nach dem Maschensatz und dem Ohmschen Gesetz gilt

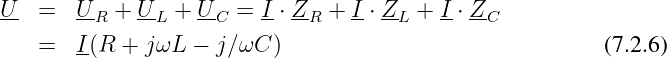
U- = UR + UL + U-C = I-⋅ ZR + I-⋅ ZL + I-⋅ ZC = I(R + jωL − j∕ωC ) (7.2.6)

Impedanz:

Division durch den Strom I ergibt identisch

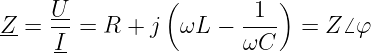( ) Z = U-= R + j ωL − -1-- = Z⁄-φ -- I- ωC

(7.2.7)

Leistungen:

Beachten: Rechenregeln für komplexe Zahlen! Bezugszeiger Strom, konjugiert komplexer Strom I^∗.

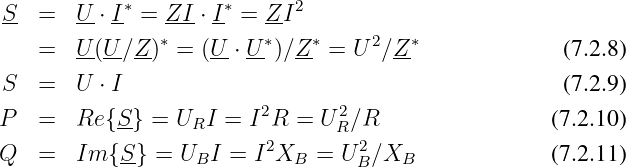
S- = U-⋅ I∗ = ZI-⋅ I∗ = ZI2 ∗ ∗ ∗ 2 ∗ = U(U-∕Z-) = (U- ⋅ U )∕Z-- = U ∕Z- (7.2.8) S = U ⋅ I (7.2.9) 2 2 P = Re{S-} = URI = I R = U R∕R (7.2.10) Q = Im {S} = UBI = I2XB = UB2∕XB (7.2.11)

Spannungen:

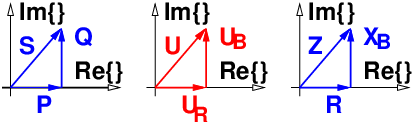
Es ergeben sich ähnliche Dreiecke für die Spannungen wegen

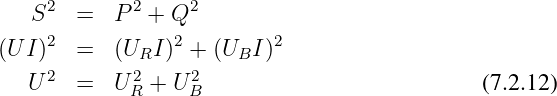
S2 = P 2 + Q2 2 2 2 (UI ) = (URI ) + (UBI ) U2 = UR2+ U 2B (7.2.12)

Widerstände:

Es ergeben sich ähnliche Dreiecke für die Widerstände wegen

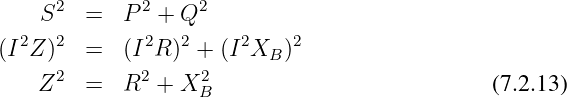
S2 = P 2 + Q2 2 2 2 2 2 2 (I Z) = (I R) + (I XB ) Z2 = R2 + X2B (7.2.13)

Abbildung 7.2.2: Ähnliche Dreiecke für Leistungen, Spannungen und Impedanzen

→ Die gezeichneten Zeigerdiagramme in Abb. 7.2.2 unterscheiden sich nur durch den Maßstabsfaktor!

Impedanzen:: Gegeben seien n Impedanzen Z_i = R_i + jX_i , i = 1,n in Reihenschaltung nach Abb. 7.2.3 .

Abbildung 7.2.3: Addition von beliebigen Impedanzen bei einer Reihenschaltung: (a) Schaltbild, (b) Zeigerdiagramm für Widerstände
Addition:: Mit den Rechenregeln der komplexen Zahlen folgt direkt
$Z- = Z1 + Z2 + ...+ Zn = R1 + R2 + ...+ Rn + j(X1 + X2 + ...+ Xn ) ∑n ∑n = Ri + j Xi (7.2.14) i=1 i=1$
mit X_i = X_{L_i} = ωL_i oder X_i = X_{C_i} = −1∕ωC_i