KenngröSSen von Schwingkreisen

8.5 Kenngrößen von Schwingkreisen

Vergleich:

Ein Vergleich der Berechnungen beim Reihen- mit dem Parallelschwingkreis zeigt ein duales Verhalten:

Der Gleichungsaufbau ist vollkommen identisch.
Um die entsprechenden Gleichungen zu überführen können wechselseitig ersetzt werden:
- Spannung U und Strom I,
- Impedanz Z und Admittanz Y ,
- Widerstand R und Leitwert G,
- Blindwiderstand X und Blindleitwert Y sowie
- Kapazität C und Induktivität L.
Es gibt nur eine identische Resonanzkreisfrequenz ω_r.
Im Resonanzfall tritt nur der Wirkwiderstand R_r = 1∕G_r nach außen in Erscheinung.
Für den Kennwiderstand und den Kennleitwert gilt X_{K_r} = 1∕B_{K_r}.

→ Einführung gemeinsamer Kenngrößen!

Frequenz:

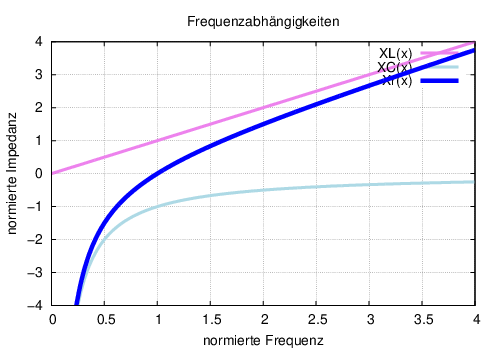
Zur besseren Darstellung der Frequenzabhängigkeit der Blindwiderstände wird die normierte Frequenz definiert zu

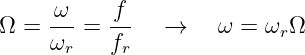ω-- -f Ω = ωr = fr → ω = ωrΩ

(8.5.1)

Damit werden z.B. die Blindwiderstände des Reihenschwingkreises zu

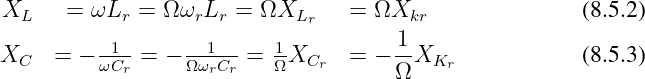
XL = ωLr = Ω ωrLr = ΩXLr = ΩXkr (8.5.2) 1 XC = − ω1Cr-= − Ωω1rCr = 1ΩXCr = − --XKr (8.5.3) Ω

X_B:

Die Abhängigkeit der Summe der Blindwiderstände wird damit

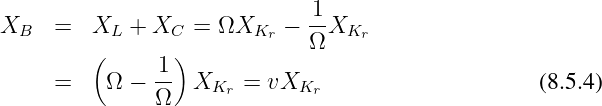
1 XB = XL + XC = ΩXKr − --XKr ( ) Ω = Ω − -1 X = vX (8.5.4) Ω Kr Kr

v:

Als relative Verstimmung wird jetzt definiert

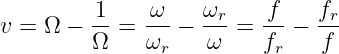1 ω ωr f fr v = Ω − --= ---− ---= -- − -- Ω ωr ω fr f

(8.5.5)

Impedanzen:

Die normierte Darstellung der Frequenzabhängigkeiten in Abb. 8.5.1 zeigt den prinzipiellen Verlauf losgelöst von tatsächlichen Schaltungswerten. ¹⁰

Abbildung 8.5.1: Normierte Frequenzabhängigkeiten der Blindwiderstände bei einem Reihenschwingkreis

B_B:

Analog ergibt sich für den Parallelschwingkreis die Abhängigkeit der Summe der Blindleitwerte zu

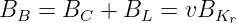B = B + B = vB B C L Kr

(8.5.6)

Normiert:

Wird die Impedanz Z der Reihenschaltung auf den Wert bei der Resonanzfrequenz normiert, so ergibt sich mit der relativen Verstimmung v

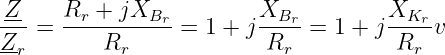-Z- = Rr-+--jXBr-= 1 + jXBr- = 1 + jXKr--v Zr Rr Rr Rr

(8.5.7)

Wird die Admittanz Y der Parallelschaltung auf den Wert bei der Resonanzfrequenz normiert, so ergibt sich analog

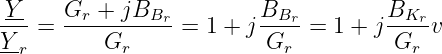Y- Gr + jBBr BBr BKr --- = ----------- = 1 + j---- = 1 + j---- v Y-r Gr Gr Gr

(8.5.8)

Güte:

Aus beiden Gleichungen kann nun die Kreisgüte, der Gütefaktor oder die Resonanzschärfe definiert werden. Beim Reihenschwingkreis erhalten wir

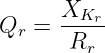Qr = XKr-- Rr

(8.5.9)

→ Die Güte ist ein Maß für die Schwingungsintensität bei Resonanz, also die Resonanzverstärkung der Spannung an den Blindkomponenten.

Beim Parallelschwingkreis erhalten wir entsprechend

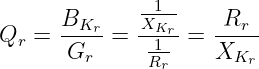BK XK1- Rr Qr = ---r = --1r = ----- Gr Rr XKr

(8.5.10)

→ Die Güte ist ein Maß für die Resonanzverstärkung des Stromes. Ein Reihen- und Parallelschwingkreis aus denselben Bauelementen hat entweder Spannungs- oder Stromresonanz, nie beides gleichzeitig¹¹.

Dämpfung:

Der Kehrwert der Kreisgüte ist die Dämpfung

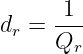1-- dr = Qr

(8.5.11)

FRAGE:

Eine gegebene RLC-Reihenschaltung mit der Impedanz Z_RLC wird an die Spanungsquelle U angeschlossen. Wie groß ist die Spannung U_RLC an der Impedanz bei der Resonanzfrequenz?

ANTWORT:

Bedeutung:

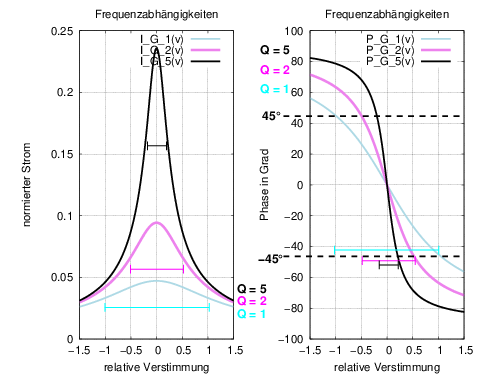
Der Amplituden- bzw. Phasengang in Abb. 8.5.2 verläuft um so steiler, je kleiner die Dämpfung d_r bzw. je größer die Güte Q_r des Kreises ist.

Abbildung 8.5.2: Definition der Bandbreite bei einem Reihenschwingkreis

Bandbreite:

Zur Objektivierung der subjektiven Beurteilung der Resonanzkurven wird die Kenngröße Bandbreite definiert

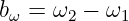bω = ω2 − ω1

(8.5.12)

bei dem der Betrag des Blindwiderstand gleich dem ohmschen Widerstand ist¹²

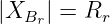|XBr | = Rr

(8.5.13)

Mit der Kreisgüte Q_r und der relativen Verstimmung v ist das bei einem Reihenschwingkreis gleichbedeutend mit

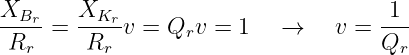XBr- XKr-- -1- R = R v = Qrv = 1 → v = Q r r r

(8.5.14)

Dieser Zusammenhang ist z.B. in Abb. 8.5.2 besonders gut sichtbar.

Strom:

Zur Bestimmung der Bandbreite aus dem Verlauf des Betrages der Schwingungsgröße gehen aus vom Strom

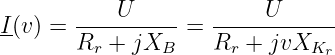U U I(v) = ----------= ------------ Rr + jXB Rr + jvXKr

(8.5.15)

Betrag:

Mit dem Betrag des Stromes bei Resonanz

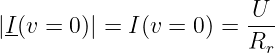|I(v = 0)| = I(v = 0) = U-- Rr

(8.5.16)

und dem Strom bei den Grenzkreisfrequenzen der Bandbreite

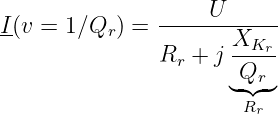I(v = 1∕Q ) = -----U------ -- r XKr-- Rr + j Qr ◟ ◝◜-◞ Rr

(8.5.17)

und dessen Betrag

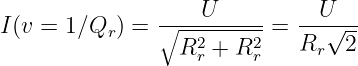U U I(v = 1 ∕Qr) = ∘----------= --√--- R2r + R2r Rr 2

(8.5.18)

erhalten wir das Verhältnis der Strombeträge beim RLC-Reihenschwingkreis zu

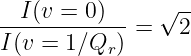I(v = 0 ) √-- ------------ = 2 I (v = 1∕Qr)

(8.5.19)

Güte:

Zur Bestimmung der Bandbreite aus der Güte bzw. der Dämpfung bei der Resonanz gehen wir von der Impedanz aus, die ihr Betragsminimum für v = 0 hat

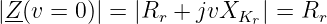|Z-(v = 0)| = |Rr + jvXKr | = Rr

(8.5.20)

Bei den beiden Grenzkreisfrequenzen ω_1,2 ist der Realteil der Impedanz gleich dem Betrag des Imaginärteils

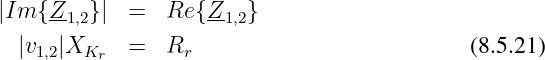
|Im {Z }| = Re {Z } -1,2 -1,2 |v1,2|XKr = Rr (8.5.21)

Mit der Güte Q_r und den Grenzkreisfrequenzen folgt dann direkt

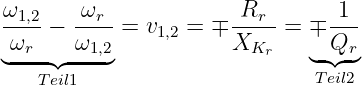ω ω R 1 -1,2-− --r- = v1,2 = ∓ --r-= ∓ --- ◟ωr--◝◜ω1,2◞ XKr ◟ ◝Q◜r◞ Teil1 T eil2

(8.5.22)

Multiplizieren mit ω_1,2ω_r ergibt die quadratische Gleichung

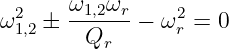ω2 ± ω1,2ωr − ω2 = 0 1,2 Qr r

(8.5.23)

Mathematik:

Die allgemeine Lösung einer quadratischen Gleichung der Form

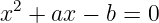2 x + ax − b = 0

(8.5.24)

ist

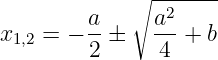∘ ------- a- a2- x1,2 = − 2 ± 4 + b

(8.5.25)

Da als Lösung nur positive Grenzfrequenzen möglich sind, entfällt die negative Wurzel. Mit den positiven Werten für die Grenzkreisfrequenzen erhalten wir die Nullstellen zu

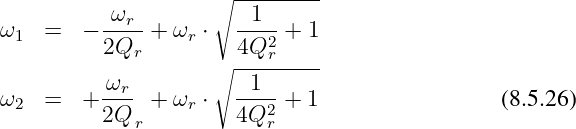
∘ --------- ω1 = − -ωr-+ ωr ⋅ -1--+ 1 2Qr 4Q2r ω ∘ -1------- ω2 = + --r + ωr ⋅ ----+ 1 (8.5.26) 2Q r 4Q2r

Elektrotechnik:

Die Bandbreite entspricht der Differenz

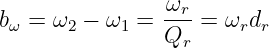ωr- bω = ω2 − ω1 = Qr = ωrdr

(8.5.27)

FRAGE:

Liegt die Resonanzfrequenz genau in der Mitte zwischen der unteren und der oberen Grenzfrequenz?

ANTWORT:

Dazu berechnen wir für den RLC-Reihenschwingkreis:


Induktivität:	L	= 67,547 H
Kapazität:	C	= 0,15 µF
Resonanzfrequenz:	f_r	=
Kennwiderstand:	X_{K_r}	=
Widerstand:	R	= 3,2 kΩ
Güte:	Q_r	=
Untere Frequenz:	f₁	=
Obere Frequenz:	f₂	=
Arithmetisches Mittel:	f′_r	=
Geometrisches Mittel:	f′_r	=

Praxis:

Aus der relativen Verstimmung v₁ = −1∕Q_r und v₂ = 1∕Q_r erhalten wir durch Gleichsetzen

− v1 = v2 ωr- ω1- ω2- ωr- ω − ω = ω − ω | ⋅ ω1 ω2ωr 2 1 2 r r 2 22 ωrω2 − ω 1ω2 = ω1 ω2 − ωrω1 ω2r(ω2 + ω1) = ω1 ω2(ω2 + ω1) 2 ω r = ω√1-ω2-- ωr = ω1 ω2 ∘ ----- fr = f1f2 (8.5.28)

FRAGE:

Können aus der Messung der Spannungsüberhöhung bei Resonanz direkt Kenngrößen von Schwingkreisen berechnet werden?

ANTWORT:

Messung:

Die Impedanz eines Reihenschwingkreises bezogen auf die Resonanzfrequenz ist

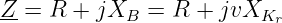Z-= R + jX = R + jvX B Kr

(8.5.29)

mit der relativen Verstimmung v und dem Kennwiderstand X_{K_r}. Die Spannung am Kondensator ist

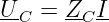U-C = ZC I-

(8.5.30)

mit dem Strom durch die Reihenschaltung

U- I-= -- Z-

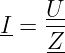(8.5.31)

und der kapazitiven Impedanz

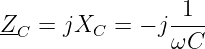ZC = jXC = − j-1-- ωC

(8.5.32)

Mit der normierten Frequenz Ω und dem Kennwiderstand X_{K_r} folgt

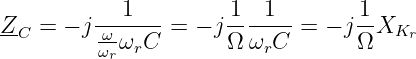1 1 1 1 ZC = − j-ω----- = − j-------= − j--XKr ωrωrC Ω ωrC Ω

(8.5.33)

Spannung:

Damit wird die Spannungsüberhöhung, das Verhältnis der Kondensatorspannung zur Quellenspannung

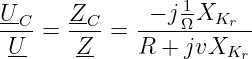U-C- ZC-- -− j-1ΩXKr-- U- = Z- = R + jvX Kr

(8.5.34)

Mit der Resonanzbedingung ω = ω_r wird die normierte Frequenz Ω = 1 und die relative Verstimmung v = 0. Dann gilt für das Spannungsverhältnis

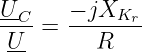UC--= −-jXKr- U- R

(8.5.35)

und für den Betrag der Spannungsüberhöhung gilt mit der Güte Q

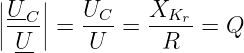||UC || UC XK ||---|| = --- = ---r-= Q U- U R

(8.5.36)

→ Analoges gilt für die Spannungsüberhöhung an der Spule, da sich die Summe der Spannungen an der Spule und dem Kondensator bei Resonanz ja zu Null addieren müssen.

¹⁰Resonanz: normierte Frequenz Ω = ω∕ω_r = 1, bzw. relative Verstimmung v = Ω − 1∕Ω = 0 und normierte Impedanz X∕X_kr = ±1.

¹¹Beim Reihenschwingkreis muss der Reihenwiderstand gegen Null gehen für eine möglichst große Güte und beim Parallelschwingkreis gegen unendlich.

¹²Oder der Phasenwinkel φ = 45^∘ beträgt

[next] [prev] [prev-tail] [front] [up]