8.3 Reihenschwingkreis

Reihe:

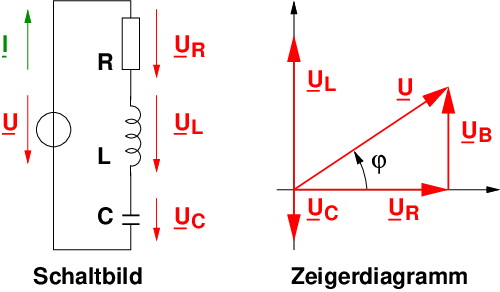
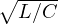Bei einem Reihenschwingkreis bezeichnet die Spannungsresonanz bei der Schaltung in Abb. 8.3.1 nur einen von drei möglichen Zuständen:

1. Strom I ist voreilend gegenüber der Spannung U
2. Strom I ist in Phase mit der Spannung U
3. Strom I ist nacheilend gegenüber der Spannung U

---

Abbildung 8.3.1: Reihen- oder Spannungsresonanz

---

Berechnung:

Für das Zeigerdiagramm lässt sich die Maschengleichung aufstellen

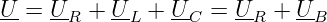(8.3.1)

Für die Teilspannungen gilt mit dem Ohmschen Gesetz

Spannung:

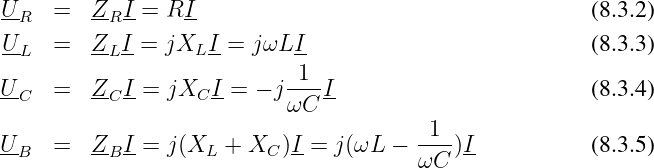
Damit gilt für die Gesamtspannung

(8.3.6)

Strom:

Für den Strom durch die Bauelemente ergibt sich durch Umstellen

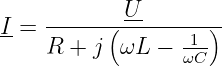(8.3.7)

Resonanz:

Es kann eine Resonanzfrequenz⁶ f_r gefunden werden mit

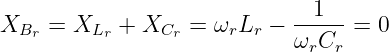(8.3.8)

Damit wird der Betrag der Impedanz Z = Z_min = R reell und minimal, d.h. der Strom I ist in Phase zur Spannung U und hat sein Maximum, wie bei der Resonanzfrequenz f_r.

ω_r:

Bei festen Bauelementewerten R_r, L_r und C_r ergibt sich dann die Resonanzkreisfrequenz oder Kennkreisfrequenz

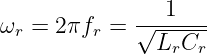(8.3.9)

X_Kr:

Mit der Resonanzkreisfrequenz kann der Kennwiderstand des Resonanzkreises definiert werden zu

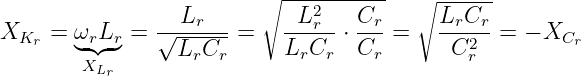(8.3.10)

Impedanzen:

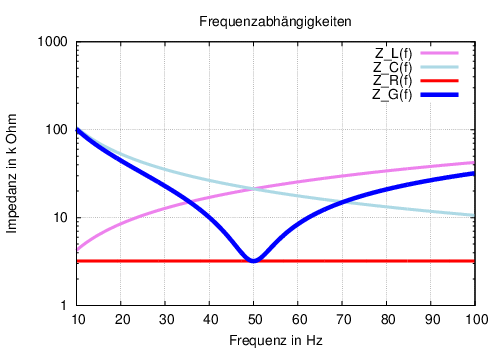
Der Verlauf des Betrages der Impedanzen als Funktion der Frequenz in Abb. 8.3.2 zeigt bei der Resonanzfrequenz ein Minimum der Gesamtimpedanz auf. ⁷

---

Abbildung 8.3.2: Frequenzabhängigkeiten des Betrags der Impedanzen bei einem Reihenschwingkreis

---