Erzwungene Schwingungen

8.2 Erzwungene Schwingungen

Ursache:

Eine erzwungene Schwingung tritt als Folge einer Spannung u = û sin(ωt) (z.B. an einem RLC-Parallelschwingkreis) oder eines Stromes i = î sin(ωt) (z.B. an einem RLC-Reihenschwingkreis) einer äußeren Quelle auf.

Wirkung:

Nach einem Einschwingvorgang stellt sich ein stationärer Zustand ein.
Die Schwingung hat die Frequenz ω der eingeprägten Spannung oder des Stromes.
Die Verluste der in den Wirkwiderständen R umgesetzte Energie P_V = i²R müssen von der Quelle zugeführt werden. Sie gehen als Wärme verloren.
Für Frequenzen ungleich der Resonanzfrequenz ω_r pendelt zusätzliche Energie zwischen dem Schwingkreis und der Quelle hin und her.
Im Resonanzfall für ω = ω_r kann eine Spannungsüberhöhung U_L∕U = U_C∕U auftreten.

Resonanz:

Spannungsüberhöhung³ bei einem Reihenschwingkreis mit Z = R_r + j(X_L + X_C) für R_r < (X_{L_r} = −X_{C_r}).

Abbildung 8.2.1: Gemessene Resonanzkurven der Spannungen und des Stroms

Maxima:

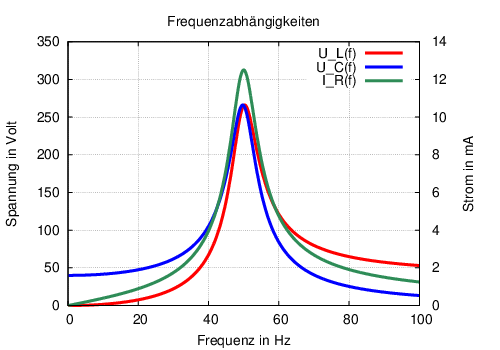
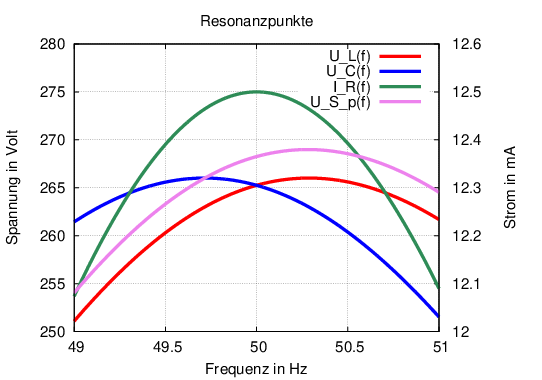
Das Maximum des Stromes liegt bei der Resonanzfrequenz, das der Kondensatorspannung tiefer und das der Spulenspannung höher, wie in Abb. 8.2.2 für den Reihenschwingkreis aus Abb. 8.2.1 .

Abbildung 8.2.2: Verschiebung der Resonanzmaxima bei einem Reihenschwingkreis

Komplex:

Die Impedanz des RCL-Reihenschwingkreises (reale Spule plus Kondensator) ist

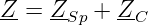Z = Z + Z -- -Sp -C

(8.2.1)

mit der Impedanz der Spule⁴

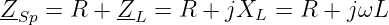ZSp = R + ZL = R + jXL = R + jωL

(8.2.2)

und der Impedanz des Kondensators

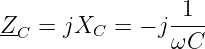Z- = jXC = − j-1-- C ωC

(8.2.3)

Strom:

Damit ergibt sich der komplexe Strom durch die Reihenschaltung zu

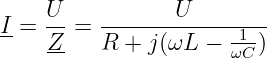U U I = -- = -------------1-- Z- R + j(ωL − ωC)

(8.2.4)

mit der Quellenspannung als Bezugspunkt, d.h. U = U.

Spannungen:

Die Spannung am Kondensator wird damit zu

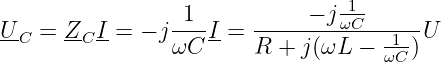-1- U-C = ZC I = − j-1-I-= -----−-jωC------U ωC R + j(ωL − ω1C-)

(8.2.5)

Die Spannung an der realen Spule wird damit zu

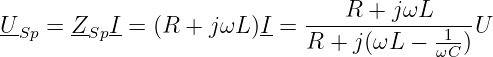R + jωL U-Sp = ZSpI-= (R + jωL )I-= -------------1--U R + j(ωL − ωC)

(8.2.6)

mit der (nicht messbaren) Teilspannung am Kupfer-Widerstand

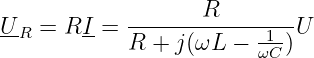-------R-------- U-R = RI--= R + j(ωL − -1-)U ωC

(8.2.7)

und der (nicht messbaren) Teilspannung an der Induktivität

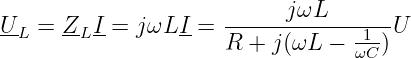jωL UL = ZLI-= jωLI--= -------------1--U R + j(ωL − ωC)

(8.2.8)

Resonanz:

Die Resonanzfrequenz f_r ist die Frequenz, bei der die Ströme und / oder Spannungen des Reihenschwingkreises ihr Betragsmaximum haben.

→ Für ihre 1. Ableitungen gilt

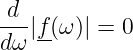d ---|f(ω)| = 0 dω

(8.2.9)

Betrag:

Für den Betrag einer komplexen Größe gilt

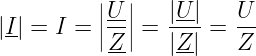|| || |I| = I = ||U-|| = |U-|= U- Z- |Z-| Z

(8.2.10)

An der Stelle, an der der Betrag einer komplexen Größe ein Maximum hat, ist auch das Quadrat dieser Größe maximal

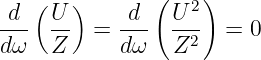( ) ( 2) -d- U- = d-- U-- = 0 dω Z dω Z2

(8.2.11)

Damit ergeben sich folgende Gleichungen und Ergebnisse

Strom:

Aus der Gln. 8.2.4 des Stromes

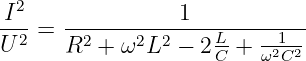2 I--= -----------1----------- U 2 R2 + ω2L2 − 2LC-+ ω12C2

(8.2.12)

folgt mit der Ableitung nach der Quotientenregel für die Funktion

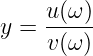u (ω ) y = ----- v(ω )

(8.2.13)

und deren Ableitung

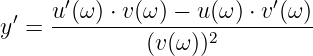′ u-′(ω)-⋅ v(ω)-−-u(ω-) ⋅ v′(ω) y = (v(ω ))2

(8.2.14)

mit den Teilfunktionen

u(ω ) = 1

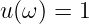(8.2.15)

und

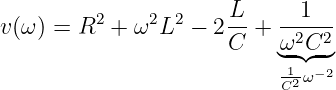L 1 v (ω ) = R2 + ω2L2 − 2-- + ------ C ω◟2C◝2◜-◞ C12ω−2

(8.2.16)

und deren Ableitungen

u′(ω ) = 0

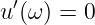(8.2.17)

und

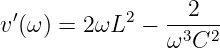v′(ω ) = 2ωL2 − --2--- ω3C2

(8.2.18)

für den Zähler

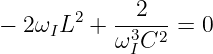2 -2---- − 2ωIL + ω3C2 = 0 I

(8.2.19)

Nach Multiplizieren mit ω_I³C²∕2

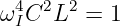4 2 2 ωIC L = 1

(8.2.20)

ergibt sich das Ergebnis zu

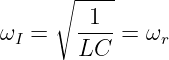∘---- ω = -1--= ω I LC r

(8.2.21)

Kondensator:

Aus der Gln. 8.2.5 der Kondensatorspannung

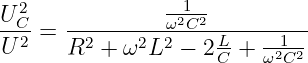UC2 -12-2 --2 = --2----2-2ωC---L----1-- U R + ω L − 2C + ω2C2

(8.2.22)

wird mit der Ableitung nach der Quotientenregel mit den Teilfunktionen

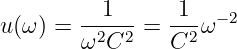1 1 u(ω ) = -2--2-= --2ω −2 ω C C

(8.2.23)

und

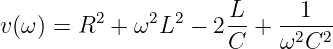v (ω ) = R2 + ω2L2 − 2L- + --1--- C ω2C2

(8.2.24)

und deren Ableitungen

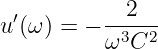′ 2 u (ω ) = − -3--2- ω C

(8.2.25)

und

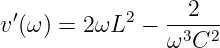2 v′(ω ) = 2ωL2 − ------ ω3C2

(8.2.26)

für den Zähler⁵

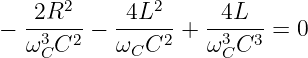-2R2-- -4L2-- -4L--- − ω3CC2 − ωC C2 + ω3CC3 = 0

(8.2.27)

Durch Multiplizieren mit ω_CC³∕2 und zusammenfassen

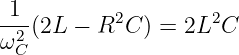1 --2(2L − R2C ) = 2L2C ωC

(8.2.28)

ergibt sich

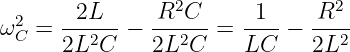2 2 2 -2L--- -R-C-- -1-- -R-- ωC = 2L2C − 2L2C = LC − 2L2

(8.2.29)

Mit

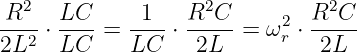R2 LC 1 R2C R2C ---2 ⋅----= ----⋅-----= ω2r ⋅----- 2L LC LC 2L 2L

(8.2.30)

ergibt sich das Ergebnis

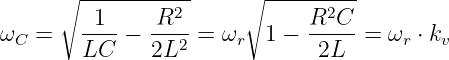∘----------- ∘ --------- -1-- -R2- R2C-- ωC = LC − 2L2 = ωr 1 − 2L = ωr ⋅ kv

(8.2.31)

als multiplikative Verschiebung der Resonanzkreisfrequenz zu tieferen Frequenzen (k_v ≤ 1) hin.

FRAGE:

Ist das Argument der Wurzel in Gln. 8.2.31 eigentlich immer positiv?

ANTWORT:

Nehmen wir eine RLC-Reihenschaltung mit R = 15 Ω, L = 0,2 H und C = 30 µF und rechnen einmal …

Resonanzkreisfrequenz $ωr =$
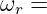
Verschiebungsfaktor $kv =$
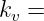
mit einer reelen Wurzel für
$R ≤$
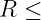
Für R > 115,47 Ω gibt es keine Schwingung mehr, da die Dämpfung zu groß ist!
Verschiebung der Resonanzkreisfrequenz beim Kondensator $ωC$
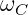
Verschiebung der Resonanzkreisfrequenz bei der Spule
→ Kommt ERST GLEICH !!!
$ωL =$
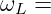
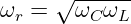
Zusammenhang $ωr = √ ωC-ωL-$

Spule:

Aus der Gln. 8.2.8 der Spulenspannung

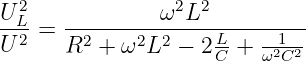U 2 ω2L2 -L-= --------------L-----1-- U 2 R2 + ω2L2 − 2C-+ ω2C2

(8.2.32)

wird mit der Ableitung nach der Quotientenregel mit den Teilfunktionen

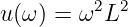2 2 u (ω ) = ω L

(8.2.33)

und

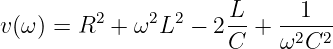L 1 v (ω ) = R2 + ω2L2 − 2-- + --2-2- C ω C

(8.2.34)

und deren Ableitungen

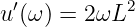u′(ω) = 2ωL2

(8.2.35)

und

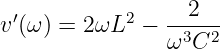v′(ω ) = 2ωL2 − --2--- ω3C2

(8.2.36)

für den Zähler

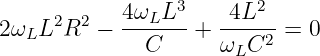2 2 4ωLL3-- -4L2-- 2ωLL R − C + ω C2 = 0 L

(8.2.37)

Durch erweitern mit ω_LC²∕2L² und zusammenfassen

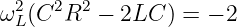2 2 2 ωL (C R − 2LC ) = − 2

(8.2.38)

ergibt sich analog zur Kondensatorspannung für die Spulenspannung

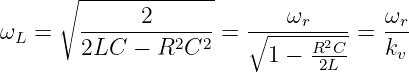∘ ------------- ω = -----2-------= ∘---ωr---- = ωr- L 2LC − R2C2 1 − R2C- kv 2L

(8.2.39)

als multiplikative Verschiebung der Resonanzkreisfrequenz zu höheren Frequenzen (1∕k_v ≥ 1) hin.

³Die Kurven aus Abb. 8.2.1 ergeben sich für die Bauelementewerte R = 3kΩ, L = 68H und C = 150nF im Freqenzbereich 0Hz ≤ f ≤ 100Hz. Bei der Resonanzfrequenz f_r = 1∕(2π √LC- ) ≈ 50Hz wird X_L = 21,362kΩ und X_C = −21,220kΩ, womit die Bedingung einer Resonanzüberhöhung erfüllt ist.

⁴Zu beachten ist, dass bei einer realen Spule anstelle von R = R_Cu und X_L nur der Scheinwiderstand der Spule Z_Sp messtechnisch zugänglich ist. In der Berechnung kann der Einfluss beider Teile jedoch separat betrachtet werden.

⁵BITTE selber einmal nachrechnen!

[next] [prev] [prev-tail] [front] [up]