-
Problem:
-
Ideale Spannungsquellen können nicht in äquivalente
Stromquellen umgewandelt werden.
-
Lösung:
-
Die allgemeine Lösung ist die Erweiterung des Verfahrens zur
modifizierten Knotenanalyse.
-
Spezialfall:
-
Analog zur Maschenanalyse können ideale Spannungsquellen
dann direkt behandelt werden, wenn Sie an einen gemeinsamen
Knoten liegen und dieser als Bezugsknoten gewählt wird.
→ Die Zeilen mit den Spannungsquellen im Lösungsvektor
entfallen, da diese ja bekannt sind.
→ Die unbekannten Ströme der Spannungsquellen können
nicht bestimmt werden.
-
Beispiel:
-
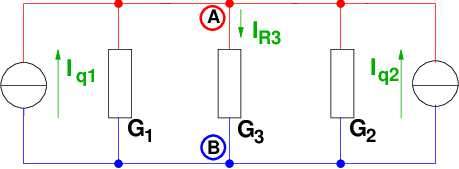
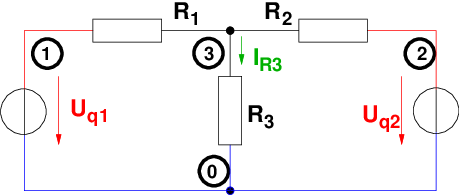
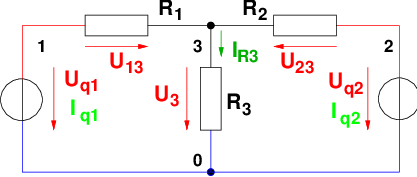
Für das T-Netzwerk mit realen Spannungsquellen führen wir
keine Umwandlung der realen Spannungsquellen in reale
Stromquellen durch wie in in Abb. 3.6.2 zu sehen ist .
→ Mit k = 4 Knoten ergibt sich ein Gleichungssystem vom
Rang k − 1 = 3, das sich auf 1 Gleichung reduziert.
-
Matrix:
-
Da die ersten beiden Zeilen der entstehenden Gleichung aufgrund
der bekannten Quellenspannungen im Lösungsvektor
gestrichen werden müssen ist die verbleibende 3. Zeile der
Gleichung
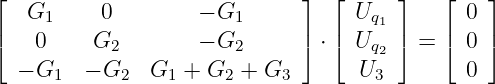 | (3.6.7) |
identisch zu Gln. 3.6.4.
-
Verfahren:
-
Beschreibungdes Netzwerkverhaltens
durch die Knotenspannungen (bezogen auf einen Masseknoten).
Die Zweigspannungen und -ströme ergeben sich aus
- den Maschengleichungen (Differenz zweier
Knotenspannungen),
- den Knotengleichungen und aus
- den Bauelementegleichungen.
-
Gleichungssystem:
-
Mit Hilfe der Kirchhoffschen Knotengleichungen ergibt sich das
Gleichungssystem
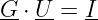 | (3.6.8) |
| | U | dem Knotenspannungsvektor |
-
Netzwerk:
-
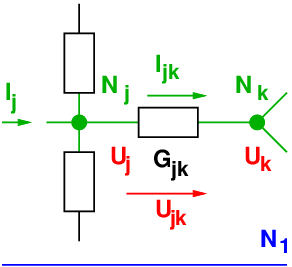
Gegeben sei das Netzwerk in Abb. 3.6.3 aus N Knoten mit den
Zweigströmen Ijk, den Zweigspannungen Ujk und den Leitwerten
Gjk.
-
Voraussetzung:
-
Dem Knoten Nj wird der Strom Ij eingeprägt.
-
Frage:
-
Welche Spannungen Uk1 = Uk − U1 entstehen an den Knoten Nk
?
-
Antwort:
-
Die Zweigströme werden durch die Bauelementegleichung als Funktion
der Zweigspannungen dargestellt und dann in die Kirchhoffschen
Knotengleichungen eingesetzt.
In die Kirchhoffsche Knotenregel
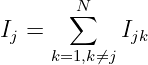 | (3.6.9) |
das Ohmsche Gesetz (Bauelementegleichung) eingesetzt
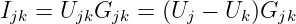 | (3.6.10) |
ergibt
-
Matrix:
-
Wir können jetzt die Einträge der Bauelemente in die Leitwertmatrix
definieren:
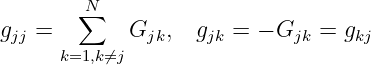 | (3.6.12) |
Setzen wir Gln. 3.6.12 in Gln. 3.6.11 ein, so erhalten wir
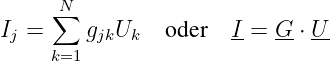 | (3.6.13) |
Es ergibt sich ein Gleichungssystem, in dem die Knotenstromsummen I
als Funktion der Knotenspannungen U dargestellt werden.
-
Lösung:
-
Die Lösung der Gleichung erhalten wir durch Inversion der
Leitwertmatrix G zu:
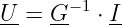 | (3.6.14) |
-
Bemerkung:
-
- Enthält die Schaltung nur passive Komponenten, so ist Y
symmetrisch
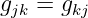 | (3.6.15) |
Bei aktiven Schaltungen kommt es aufgrund der richtungsabhängigen
Verstärkung der Schaltung zu unsymmetrischen Einträgen.
- Für die Zeilen- und Spaltensummen gilt
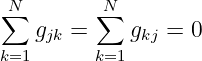 | (3.6.16) |
da sowohl in den Zeilen als auch in den Spalten jeweils der
gleiche Term positiv und negativ eingetragen wird.
- Damit G ⋅ U = I widerspruchsfrei ist, muss Y den Rang N − 1
haben.
→ Durch Streichen der Zeile und Spalte mit der Nummer des
Bezugsknotens (meistens N0, Masse) erhält man aus der
indefiniten die definite Leitwertmatrix.
Mathematisch bedeutet das, dass es unendlich viele Lösungen des
Gleichungssystems gibt, wenn G den Rang N hat, die sich
alle durch einen additiven Term bei allen Spannungen
unterscheiden. Das ist eine Eigenschaft eines Potentialfeldes, wie
wir es hier für die Spannungen der Schaltung haben.
-
Bauelemente:
-
Im folgenden werden die automatisierten Einträge der
Bauelemente in die Leitwertmatrix und dem Anregungsvektor
gezeigt.
-
Leitwerte:
-
Der Eintrag eines Leitwertes (siehe Abb. 3.6.4) erfolgt in die normale
Leitwertmatrix.
Der Eintrag in der Zeile i
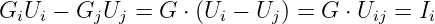 | (3.6.17) |
bedeutet, dass aus dem Knoten Ni der Strom Ii heraus fließt. Aus dem
Knoten Nj fließt der Strom −Ii heraus, bzw. der Strom Ii
hinein.
-
Stromquelle:
-
Eine Stromquelle wird mit dem Konstantstrom in den Anregungsvektor
eingetragen.
→ Liegt einer der Anschlüsse eines Bauelements am Bezugsknoten
(N0, Masse), so entfallen die Eintragungen in den entsprechenden
Zeilen und Spalten.
-
Spannungsquelle:
-
Die Bauelementegleichung einer Spannungsquelle lautet
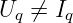 | (3.6.18) |
d.h. die Quellenspannung ist keine Funktion des Stromes
(Konstantspannungsquelle):
→ Es ist kein Eintrag von Spannungsquellen möglich, da kein
Zweig, für den der Strom nicht durch eine Bauelementegleichung als
konstanter Wert oder als Funktion einer Zweigspannung gegeben ist,
verarbeitet werden kann.
→ Abhilfe schafft die modifizierte Knotenspannungsanalyse.
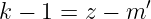
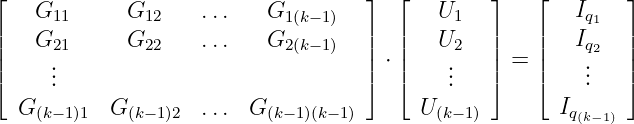
![[G11 ] ⋅ [U1] = [Iq1 + Iq2]
[G1 + G2 + G3 ] ⋅ [U1] = [Uq1G1 + Uq2G2 ] (3.6.4)](gde_1305x.png)
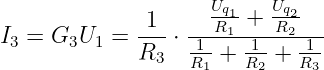
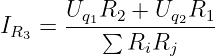
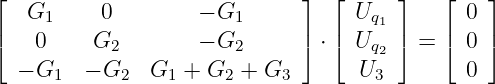
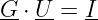
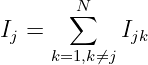
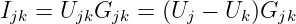
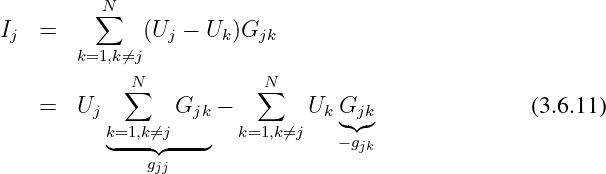
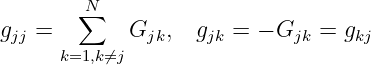
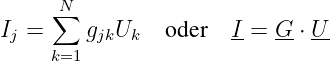
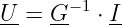
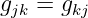
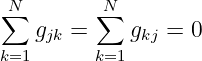
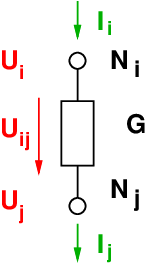
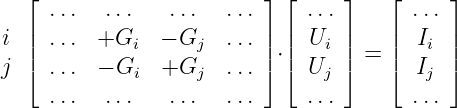
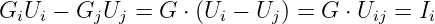
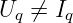
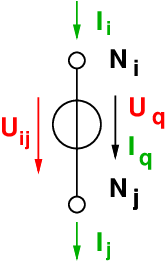
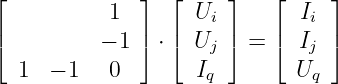
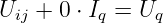
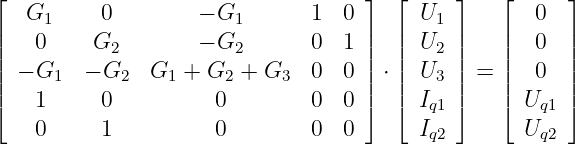
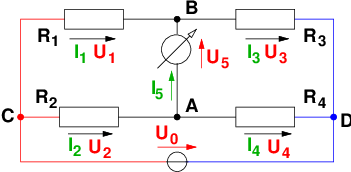
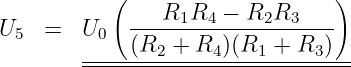
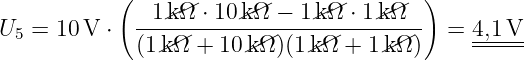
![(1/k/Ω ⋅ 10/k/Ω − 1/k/Ω ⋅ 1/k/Ω ) ⋅ 10V
I5 = -------------------/------/------⋅⋅⋅
(1 kΩ + 1 kΩ )[1/kΩ ⋅ 10/kΩ+
⋅⋅⋅------------------------------------------------
10/k/Ω(1//kΩ + 10//kΩ )] + 1/k/Ω ⋅ 1/k/Ω (1k Ω + 10 kΩ)
= 0,3585 mA
-----------](gde_1332x.png)