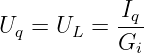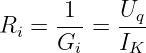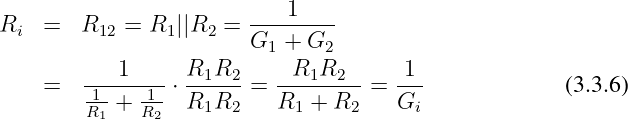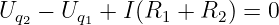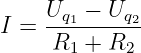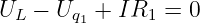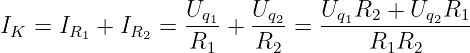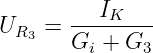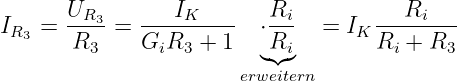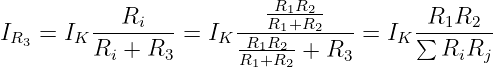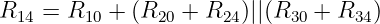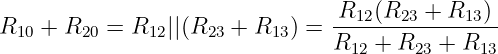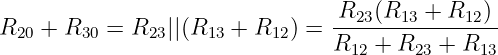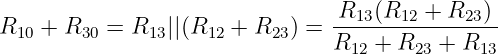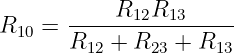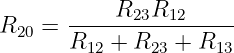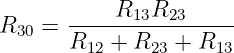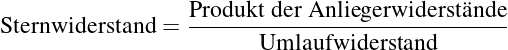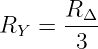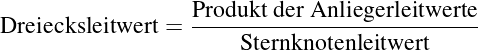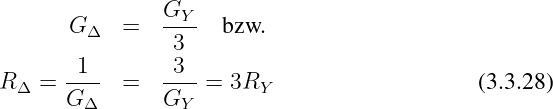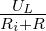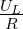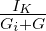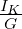3.3 Ersatzquellen

ESQ:

Jedes beliebige lineare, aktive Netzwerk mit 2 Anschlussklemmen (also ein Zweipol wie in Abb. 3.3.1) kann bezüglich dem elektrischen Verhalten an diesen 2 Anschlussklemmen durch eine Ersatzquelle ersetzt werden.

→ Somit haben alle 3 Netzwerke den selben Strom I_R3 und die selbe Spannung U_R3 am Widerstand R₃.

---

Abbildung 3.3.1: Netzwerkberechnung mit Ersatzquellen

---

Leerlauf:

Zur Bestimmung der Werte der Ersatzquellen wählen wir den Widerstand R₃ = ∞ und erhalten dafür mit der Leerlaufspannung U_L = U_AB die Quellenspannung der Ersatzspannungsquelle zu

(3.3.1)

Kurzschluss:

Für den Widerstand R₃ = 0 erhalten mit dem Kurzschlussstrom I_K = I_AB den Quellenstrom der Ersatzstromquelle zu

(3.3.2)

Innenwiderstand:

Bei beiden Ersatzquellen ergibt das Ohmsche Gesetz den Innenwiderstand der Quellen zu

(3.3.3)

Thévenin:

Mit dem Theorem der Ersatzspannungsquelle ergibt sich der gesuchte Strom zu

(3.3.4)

Norton:

Mit dem Theorem der Ersatzstromquelle ergibt sich der gesuchte Strom I_R3 = U_R3∕R₃ mit der Spannung

(3.3.5)

3.3.1 Beispiel zu Ersatzquellen

Innenwiderstand:

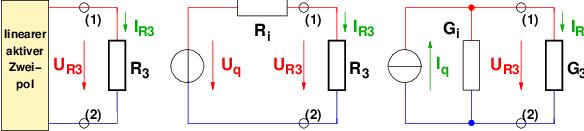
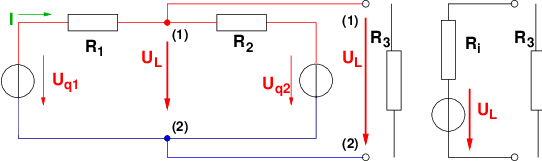
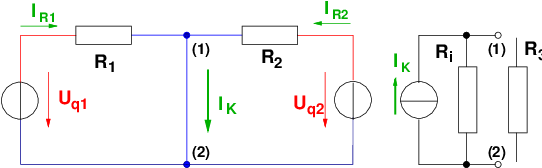
Für das T-Netzwerk des Beispiels benötigen wir den Innenwiderstand zwischen den Punkten (1) und (2) ohne den Widerstand R₃.

→ Spannungsquellen werden kurzgeschlossen und Stromquellen entfernt!

---

Abbildung 3.3.2: Berechnung des Innenwiderstandes von Ersatzquellen

---

E-Spannungs-Q:

Für das Verfahren mit der Ersatzspannungsquelle benötigen wir als nächstes die Leerlaufspannung zwischen den Punkten (1) und (2) ohne den Widerstand R₃.

---

Abbildung 3.3.3: Berechnung der Leerlaufspannung der Ersatzspannungsquelle

---

Aus der großen Masche in Abb. 3.3.3 erhalten wir den Strom mit

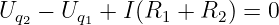(3.3.7)

zu

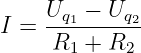(3.3.8)

Aus der linken Masche erhalten wir die Leerlaufspannung mit

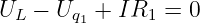(3.3.9)

zu

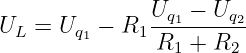(3.3.10)

Für einen Vergleich der Ergebnisse benötigen wir eine passende Umformung

Thévenin:

Mit dem Thévenin-Theorem ergibt sich der gesuchte Strom zu

Kann die Berechnung auch alternativ mir dem Verfahren der Ersatzstromquelle nach Norton durchgeführt werden? Die hypothetische Antwort sollte jeder geben können, die Überprüfung ist dann eine reine „Zeitfrage“.

E-Strom-Q:

Für das Verfahren mit der Ersatzstromquelle benötigen wir alternativ den Kurzschlussstrom zwischen den Punkten (1) und (2) ohne den Widerstand R₃.

---

Abbildung 3.3.4: Berechnung des Kurzschlussstromes der Ersatzstromquelle

---

Strom:

Für den Knoten (1) in Abb. 3.3.4 erhalten wir den Strom zu

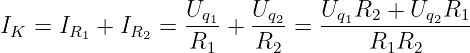(3.3.13)

Norton:

Nach dem Norton-Theorem kann der gesuchte Strom mit der Spannung

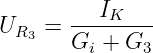(3.3.14)

berechnet werden zu

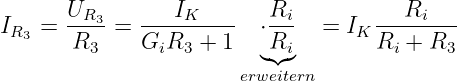(3.3.15)

Mit einem Stromteiler erhalten wir den gesuchten Strom aber ebenso zu

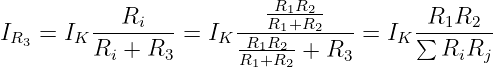(3.3.16)

Mit dem berechneten Kurzschlussstrom ergibt sich wieder das bereits mehrfach erhaltene Ergebnis zu

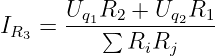(3.3.17)

q.e.d.

3.3.2 Stern-Dreieck-Umwandlung

Problem:

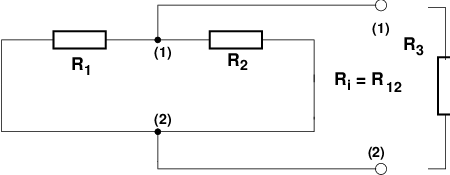
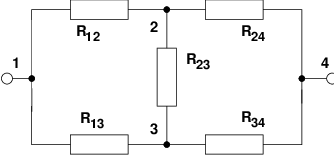
Bei der Berechnung der Innenwiderstände kann es vorkommen, dass sich die Widerstände nicht durch Reihen- oder Parallelschaltung zusammenfassen lassen, wie in Abb. 3.3.5 für den Widerstand R₁₄ zu sehen ist .

---

Abbildung 3.3.5: Problemschaltung zur Zusammenfassung von Widerständen

---

→ Es liegen keine 2 Widerstände an der gleichen Spannung

→ Es werden keine 2 Widerstände vom gleichen Strom durch flossen

Ansatz:

Zur Lösung des „Problems“ wird das Netzwerk so umgezeichnet, dass vorhandene Dreieck- und/ oder Sternschaltungen sichtbar werden.

Lösung:

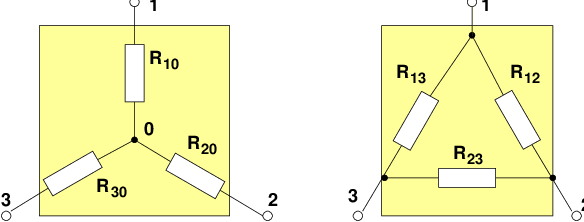
Im vorhandenen Netzwerk ergeben sich 2 Dreieckschaltungen, dessen linkes Dreieck Δ₁₂₃ in eine äquivalente Sternschaltung Y ₁₂₃ wie in Abb. 3.3.6 umgewandelt werden kann.

---

Abbildung 3.3.6: Umgewandelte Schaltung zur Zusammenfassung von Widerständen

---

Ergebnis:

In der umgewandelten Schaltung berechnet sich der Ersatzwiderstand nun wieder nach den bekannten Regel der Reihen- und Parallelschaltung zu

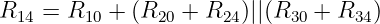(3.3.18)

Frage:

Wann sind die Stern- und Dreieckschaltung äquivalent?

Ansatz:

Wenn beide Schaltungen in Abb. 3.3.7 nach außen gleich sein sollen, so müssen die Widerstände zwischen den Knoten identisch sein.

---

Abbildung 3.3.7: (Dreier-) Stern- und Dreieck-Schaltung

---

Knoten 1-2:

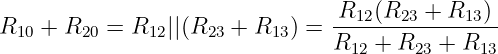(3.3.19)

Knoten 2-3:

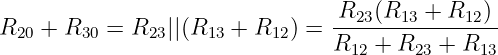(3.3.20)

Knoten 1-3:

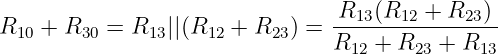(3.3.21)

Dreieck → Stern:

Addition von Gln. 3.3.19 und Gln. 3.3.21 und Subtraktion von Gln. 3.3.20 liefert die Umwandlungsgleichung

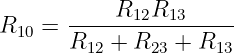(3.3.22)

Einsetzen in Gln. 3.3.19 ergibt

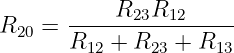(3.3.23)

und in in Gln. 3.3.21 ergibt

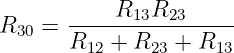(3.3.24)

Ergebnis:

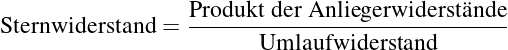(3.3.25)

Symmetrie:

Als Sonderfall für R₁₂ = R₁₃ = R₂₃ erhält man

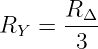(3.3.26)

Stern → Dreieck:

Ausgehend von den Ergebnissen der Dreieck-Stern-Transformation ergibt sich folgendes Ergebnis (wobei die Herleitung mit den bereits bekannten Methoden der Mathematik für jeden möglich ist, oder?) :

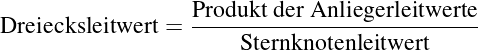(3.3.27)

→ Der Umlaufwiderstand ist die Summe der Widerstände in einer Masche.

→ Der Knotenleitwert ist die Summe der Leitwerte in einem Knoten.

Symmetrie:

Als Sonderfall für G₁₀ = G₂₀ = G₃₀ erhält man analog

3.3.3 Bewertung der Ersatzquellen

Bewertung:

Anwenden der Ersatzquellen

• NEGATIV: Mit den Ersatzquellen kann immer nur eine Spannung oder ein Strom eines passiven Zweiges berechnet werden. Zur Berechnung aller Unbekannten ist das Verfahren zu aufwendig.
• Die Berechnung der Leerlaufspannung oder des Kurzschlussstromes erfolgt i.a. mit Hilfe der Kirchhoffschen Gleichungen.
• Zur Berechnung der Innenwiderstände muss ggf. eine Stern-Dreieck-Umwandlung durchgeführt werden.
• POSITIV: Das Thévenin-Theorem ist besonders einfach, wenn R_i ≪ R ist, da dann näherungsweise I_AB = ≈ gilt.
• POSITIV: Das Norton-Theorem ist besonders einfach, wenn G_i ≪ G ist, da dann näherungsweise U_AB = ≈ gilt.