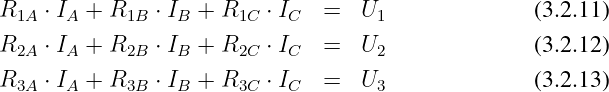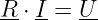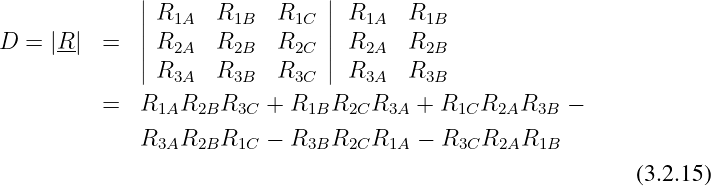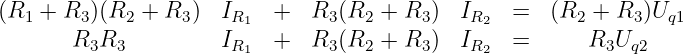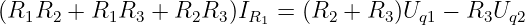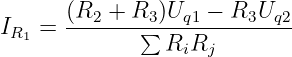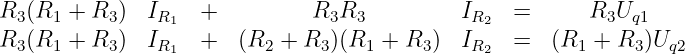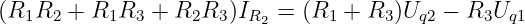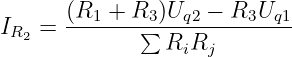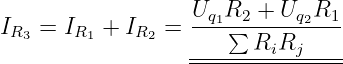-
Aufgabe:
-
Gegeben sei ein
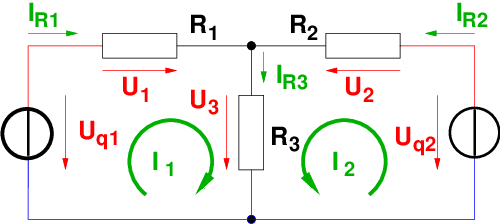
Netz aus Abb. 3.2.1 mit zwei Spannungsquellen. Der Strom I3
durch den Widerstand R3 soll analytisch bestimmt werden!
→ Reichen die bekannten Methoden aus? Ja!
-
Lösung:
-
Anwendung des Ohmschen Gesetzes und der Kirchhoffschen
Gleichungen zur Bestimmung der 6 Unbekannten:
- 3 Spannungen U1, U2 und U3 und
- 3 Ströme IR1, IR2 und IR3.
-
Aufgabe:
-
Für die 6 Unbekannten werden 6 unabhängige Gleichungen benötigt.
Wie findet man sie?
-
Netzwerk:
-
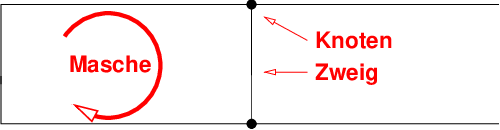
Ein elektrisches Netzwerk besteht aus z Zweigen, die an den k Knoten
miteinander verbunden sind und somit m Maschen bilden. In
Abb. 3.2.2 sind für die Schaltung aus Abb. 3.2.1 Zweige, Knoten und
Maschen gezeichnet.
- An einem Knoten sind mindestens 3 Zweige
angeschlossen.
- Ein Zweig verbindet 2 Knoten miteinander wobei alle
Bauelemente vom selben Strom durch flossen werden.
- Eine Masche ist ein geschlossener Weg über Zweige und
Knoten.
-
Frage 1:
-
Wie viele Zweige, Knoten und Maschen enthält die Beispielschaltung
aus Abb. 3.2.1 ?
- Zweige: z = 3, zwischen je zwei Punkten
- Knoten: k = 2, die beiden schwarzen Punkte
- Maschen: m = 3, links, rechts und außen herum
→ Damit ergeben sich 2 Knotengleichungen, 3 Maschengleichungen
und 3 Gleichungen aus dem Ohmschen Gesetz, also 8 Gleichungen für
6 Unbekannte.
-
Frage 2:
-
Welche der 8 Gleichungen sind linear unabhängig?
- Aus dem Ohmschen Gesetz für jeden Zweig ergeben sich
z = 3 unabhängige Gleichungen.
- Bei k = 2 Knoten ist k − 1 = 1 Knotengleichung linear
unabhängig.
- Also müssen von den Maschengleichungen
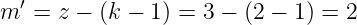 | (3.2.1) |
unabhängig sein!
-
Frage 3:
-
Wie findet man alle linear unabhängigen Maschengleichungen?
→ In dem einfachen Beispiel kann eine beliebige der 3 Maschen
weggelassen werden.
-
Praxis:
-
Eine praktische Methode zur Auswahl unabhängiger Maschen
ist:
Nach Auswahl einer Masche trennt man diese Masche in einem
beliebigen Zweig auf. Weitere Maschen dürfen keine aufgetrennten
Zweige enthalten. Es werden so viele Maschen gebildet wie möglich
sind.
-
Ohmsches Gesetz:
-
3 Gleichungen
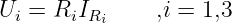 | (3.2.2) |
-
Maschenregel:
-
2 Gleichungen
-
Knotenregel:
-
1 Gleichung
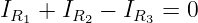 | (3.2.4) |
-
Mathematik:
-
Zur Berechnung der Zweigströme erhält man ausgehend von den
Maschengleichungen
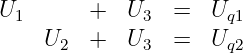 | (3.2.5) |
Mit dem Ohmschen Gesetz folgt
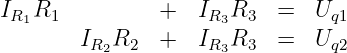 | (3.2.6) |
Mit der Knotengleichung kann der Strom I3 eliminiert werden
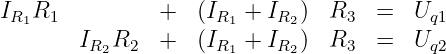 | (3.2.7) |
Ordnet man diese Gleichungen nach den beiden Unbekannten, so ergibt
sich folgendes Gleichungssystem
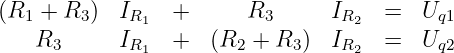 | (3.2.8) |
oder in Matrizenschreibweise
![[ ] [ ] [ ]
R1 + R3 R3 ⋅ IR1 = Uq1
R3 R2 + R3 IR2 Uq2](gde_1233x.png) | (3.2.9) |
-
Ergebnis:
-
Die Untersuchung eines linearen Netzes führt zu einem linearen
Gleichungssystem für die Unbekannten (Ströme), das nun nur noch
aufgelöst werden muss.
→ Anwenden mathematischer Methoden, heute mit Taschenrechner
direkt lösbar.
-
Matrizen:
-
Für alle, die noch keine Matrizenrechnung kennen kommt hier die
minimal notwendige Mathematik. Die Schreibweise mit der
3×3-Matrix
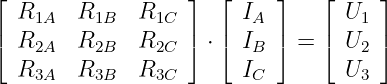 | (3.2.10) |
ist nur eine verkürtzte Schreibweise für das Gleichungssystem mit den
drei Gleichungen
in der beispielhaft die Elemente Rij der Matrix mit den Komponenten
Ij des Ergebnisvektors multipliziert werden.
-
Rang:
-
Das lineare Gleichungssystem
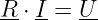 | (3.2.14) |
ist genau dann eindeutig lösbar, wenn der Rang der Matrix R gleich
der Anzahl der Zeilen der Matrix ist. Dann ist aber auch die
Determinate der Matrix ungleich Null.
→ Alle Gleichungen sind linear unabhängig!
-
Determinaten:
-
Die Determinante einer 3 × 3-Koeffizientenmatrix R berechnet sich
aus dem Produkt der Hauptdiagonalen minus dem Produkt der
Nebendiagonalen zu
-
Gauß:
-
Für die Lösung des linearen Gleichungssystems 3.2.8 mit dem
gaußschen Eliminationsverfahren wird die Koeffizientenmatrix in
Dreiecksform gebrach.
Wir multiplizieren daher die 1. Zeile mit (R2 + R3) und die 2. Zeile mit
R3
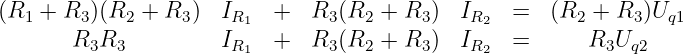 | (3.2.16) |
Wenn wir nun die 2. Zeile von der 1. subtrahieren
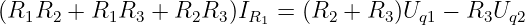 | (3.2.17) |
-
1. Strom:
-
erhalten wir nun den 1. Teilstrom zu
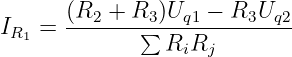 | (3.2.18) |
Für die Berechnung des 2. Teilstromes multiplizieren wir nun die 1.
Zeile mit R3 und die 2. Zeile mit (R1 + R3)
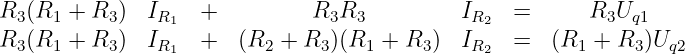 | (3.2.19) |
Wenn wir nun die 1. Zeile von der 2. subtrahieren
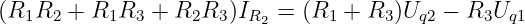 | (3.2.20) |
-
2. Strom:
-
erhalten wir den 2. Teilstrom zu
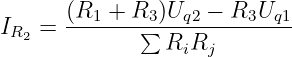 | (3.2.21) |
Der gesuchte Strom IR3 ist dann die Summe dieser beiden
Ströme
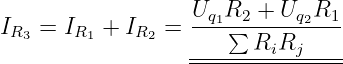 | (3.2.22) |
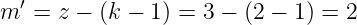
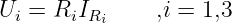

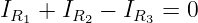
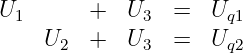
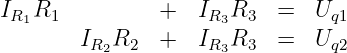
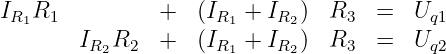
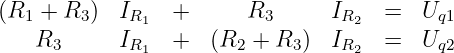
![[ ] [ ] [ ]
R1 + R3 R3 ⋅ IR1 = Uq1
R3 R2 + R3 IR2 Uq2](gde_1233x.png)