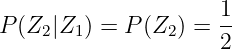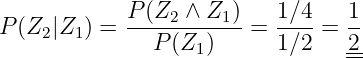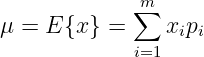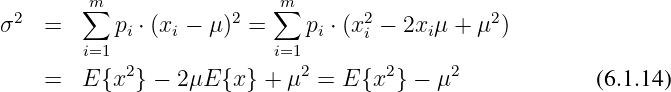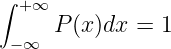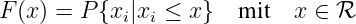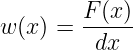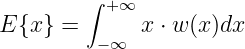Wahrscheinlichkeitslehre

[next] [prev] [prev-tail] [tail] [up]

6.1 Wahrscheinlichkeitslehre

Shannon:

Claude Elwood Shannon lieferte in den 1940er bis 1950er Jahren wesentliche Beiträge zur ¹

Theorie der Datenübertragung und der Wahrscheinlichkeitstheorie.

Er fragte sich, wie man eine verlustfreie Datenübertragung über Kanäle sicherstellen kann. Dabei geht es auch darum, die Datensignale vom Hintergrundrauschen zu trennen.
Außerdem will man, während der Übertragung aufgetretene Fehler erkennen und korrigieren. Dazu ist es notwendig, zusätzliche redundante (d. h. keine zusätzliche Information tragenden) Daten mitzusenden, um dem Empfänger eine Datenverifikation oder Datenkorrektur zu ermöglichen.

Behauptung:

Die Wahrscheinlichkeitslehre bildet die Grundlage der modernen Gesellschaft

→Lotto, Wetten, TV-Werbespielsendungen.

Beispiel 6.1.1 (3 Tore)

In einer Werbesendung werden 3 Garagentore präsentiert, wobei hinter einem ein zu gewinnendes Auto steht und die beiden anderen eine Niete („Zonk“) sind:²

Wie groß ist die Gewinnchance, wenn der Spieler sich eines der 3 Tore aussuchen darf?
Nachdem der Spieler sich ein Tor ausgesucht hat, öffnet der Moderator ein Tor mit einer Niete.
Der Spieler bekommt die Chance, entweder sein gewähltes Tor zu behalten oder zu wechseln.
Wie groß sind die Gewinnchancen der beiden verbliebenen Tore?

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Zahlenwerte sind:

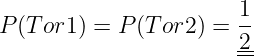
Gewinnchance $1 P (Tor1 ) = P(T or2) = -- 2-$
—
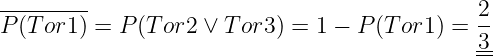
Gewinnchancen $--------- 2 P (T or1) = P (Tor2 ∨ T or3) = 1 − P (Tor1) = -- -3$

Bedeutung:

Die Wahrscheinlichkeitslehre bildet die Grundlage der modernen Nachrichtentechnik

→Übertragungstechnik und Vermittlungstechnik.

Zufallsexperiment:

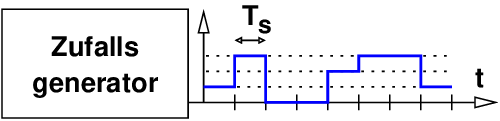
Ein idealer Zufallsgenerator erzeuge an seinem Ausgang ein vierstufiges Zufallssignal wie Abb. 6.1.1 dargestellt .

Abbildung 6.1.1: Erzeugen eines 4-stufigen Zufallssignals

Ereignis:

Ein Experiment liefert genau einen Wert, das Ereignis x ∈ H aus der Menge aller möglichen Ereignisse H = {0, 1, 2, 3}. In einer Beobachtungszeit T_B treten die Ereignisse x_k ∈ E auf aus dem Ereignisfeld, der Menge der eingetretenen Ereignisse E ∈ H des Experiments.

Häufigkeit:

Betrachtet man nicht die Folge der Ereignisse x_k(t), sondern fragt nach der relativen Häufigkeit, mit der ein bestimmtes Ereignis aufgetreten ist, so erhält man

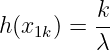h(x ) = k- 1k λ

(6.1.1)

wenn das Ereignis x_1k = 1 genau k-mal von insgesamt λ Ereignissen aufgetreten ist.

Grenzwert:

Bildet man den Grenzwert für λ →∞ so erhält man die statistische Wahrscheinlichkeit zu

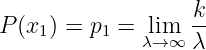k P (x1) = p1 = lim -- λ→ ∞ λ

(6.1.2)

Die 4 möglichen Ereignisse x₀, x₁, x₂ und x₃ bei einem idealen Zufallgenerator sind alle gleich wahrscheinlich

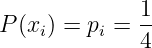P (x ) = p = 1- i i 4

(6.1.3)

Addition:

Die Wahrscheinlichkeit, dass entweder x₀ ODER x₁ ODER x₂ eintritt, ist dann

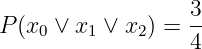3- P(x0 ∨ x1 ∨ x2) = 4

(6.1.4)

Daraus lässt sich das Additionsgesetz der Wahrscheinlichkeiten für unabhängige Zufallsereignisse herleiten

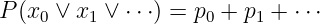P (x0 ∨ x1 ∨ ⋅⋅⋅) = p0 + p1 + ⋅⋅⋅

(6.1.5)

Summe:

Die Summe der Wahrscheinlichkeiten von Ereignissen in einem vollständigen System ist immer

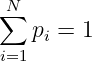∑N pi = 1 i=1

(6.1.6)

Negativ:

Tritt bei einem Experiment das Ereignis x_i mit der Wahrscheinklichkeit p(x_i) auf, so tritt es nicht auf mit der Wahrscheinlichkeit

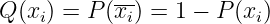Q (xi) = P(xi) = 1 − P (xi)

(6.1.7)

Bedingt:

Die bedingte Wahrscheinlichkeit beschreibt das Ereignis x_i unter der Bedingung, dass vorher das Ereignis y_i sicher eingetreten ist

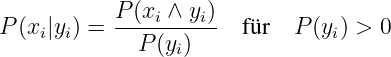P(xi ∧ yi) P(xi|yi) = ---------- für P (yi) > 0 P (yi)

(6.1.8)

Sind aber die Ereignisse x_i und y_i statistisch unahhängige Ereignisse, so folgt mit

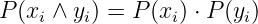P (xi ∧ yi) = P(xi) ⋅ P(yi)

(6.1.9)

direkt wieder

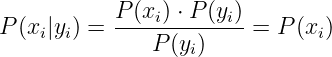P (x |y) = P-(xi) ⋅ P-(yi) = P (x ) i i P (yi) i

(6.1.10)

Multiplikation:

Daraus lässt sich das Multiplikationsgesetz der Wahrscheinlichkeiten für unabhängige Zufallsereignisse herleiten

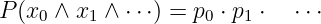P (x0 ∧ x1 ∧ ⋅⋅⋅) = p0 ⋅ p1 ⋅ ⋅⋅⋅

(6.1.11)

Beispiel 6.1.2 (2 Münzen)

Es werden zwei Münzen mit den Seiten Kopf (K) und Zahl (Z) geworfen. Dann können insgesammt 4 verschiedene Ereignisse eintreten:

KK, KZ, ZK, ZZ

Wie groß ist die bedingte Wahrscheinlichkeit, dass sich beim Wurf der zweiten Münze eine Zahl ergibt, wenn beim Wurf der ersten Münze bereits eine Zahl eingetreten ist³?

Hinweis: Da beide Ereignisse voneinander unabhängig sind muss sich natürlich

1 P (Z2|Z1) = P (Z2) = -- 2

(6.1.12)

ergeben. Hier ist also die Anwendung der Formel zur Berechnung der bedingten Wahrscheinlichkeit gefragt!

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Zahlenwerte sind:

Bedingte Wahrscheinlichkeit

P (Z |Z ) = P-(Z2-∧-Z1) = 1∕4-= 1- 2 1 P(Z1 ) 1∕2 2-

Parameter:

Für (diskrete) Zufallsprozesse sind folgende Parameter von besonderer Bedeutung⁴:

Der Erwartungswert E{x} oder Scharmittelwert μ eines diskreten Zufallssignals⁵

∑m μ = E {x} = xipi i=1

(6.1.13)

Die Varianz oder die daraus berechnete Standardabweichung σ ist ein Maß für die Größe der Abweichung vom Mittelwert
$2 m∑ 2 ∑m 2 2 σ = pi ⋅ (xi − μ) = pi ⋅ (x i − 2xiμ + μ ) i=1 2 i=12 2 2 = E {x } − 2μE {x} + μ = E{x } − μ (6.1.14)$

Beispiele:

Wichtige Zufallsprozesse sind - Gleichverteilung mit p_i = const - Binominal-Verteilung bzw. Bernoulli-Verteilung bzw. Newton-Verteilung

Kontinuierlich:

Neben den diskreten Zufalsssignalen gibt es noch kontinuierliche Zufallssignale, z.B.

Sprachsignal
→ Wäre der nächste Zeitwert eines Sprachsignals nicht zufällig sondern ließe sich aus den vergangenen Werten berechnen dann enthielt das Signal keine neue Information mehr für die Zukunft und brauchte nicht übertragen zu werden, sondern könnte aus den Werten der Vergangenheit berechnet werden.
Videosignal, s.o.
Thermisches Rauschen (von Widerständen)

Summe:

Anstelle der Wahrscheinlichkeit p_i = P(x_i) wird die Wahrscheinlichkeit P(x) verwendet mit

∫ +∞ − ∞ P(x)dx = 1

(6.1.15)

Funktion:

Für die Wahrscheinlichkeitsverteilung F(x) einer Zufallsvariablen x

F (x) = P {xi|xi ≤ x } mit x ∈ ℛ

(6.1.16)

ist die Wahrscheinlichkeitsdichte w(x) die Ableitung

F (x ) w (x ) = ----- dx

(6.1.17)

und der Erwartungswert E{x} der Zufallsvariablen x mit der Wahrscheinlichkeitsdichte w(x)

∫ +∞ E{x } = x ⋅ w (x)dx −∞

(6.1.18)

¹Es ist zweifelhaft und wurde auch von Shannon nicht beansprucht, dass seine Studie „A Mathematical Theory of Communication“ (Informationstheorie) von substantieller Bedeutung für Fragestellungen außerhalb der Nachrichtentechnik ist. Sie zeigt den Trend zur Verwissenschaftlichung der Technik, der zur Bildung der Ingenieurwissenschaften führte.

²Wem das Beispiel zu einfach ist, der kann es auf Lotto übertragen: Der Spieler füllt einen Tippschein aus. Allle anderen Kombinationen füllt der Moderator aus. Es erfolgt eine geheime Ziehung. Der Moderator behält nur den einen Schein, der 6 Rcihtige hat, falls er ihn hat. Sollte der Spieler seinen Tippschein gegen den des Moderators tauschen?

³Man kann diese Fragestellungen noch beliebig ergänzen: Ist die Wahrscheinlichkeit n-mal eine Zahlenfolge zu haben genauso groß, wie (n+1)-mal eine Zahlenfolge zu haben? Sicher nicht, oder? Dann müsste aber nach einer Folge von n Zahlen, die Wahrscheinlichkeit einen Kopf zu haben größer sein. Das würde aber bedeuten, dass diese „Quelle“ ein Gedächtnis hätte. Letzendlich ist aber die Aussage, “die Quelle hat eine gleiche Wahrscheinlichkeit für Kopf und Zahl“ ein Gedächtnis, oder? Ähnliche Überlegungen werden immer wieder beim Roulette-Spiel verwendet, um auf Schwarze oder Rote Zahlen wetten zu können. Dabei verliert man beim Roulette aber sicher, da es noch eine grüne Zahl gibt!

⁴Was bedeuten diese beiden Parameter bei einer Gaußkurve? Zeichnen Sie einmal diese Kurve und kennzeichnen Sie dann den Erwartungswert und die Standardabweichung.

⁵Versuchen Sie einmal den Erwartungswert beim Würfeln zu berechnen. Die Lösung ist 3,5.

[next] [prev] [prev-tail] [front] [up]