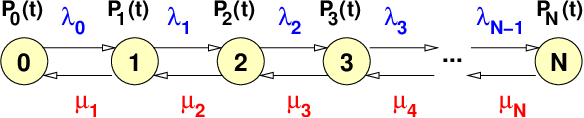
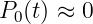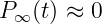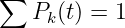Durch Messen der Belegungen der Leitungen eines TK-Systems kann man die Statistik der Belegungsdauer TB angeben. Für diesen gedächtnislosen Bedienprozess erhält man eine (negative) Exponentialverteilung für Belegungszeiten größer als TB
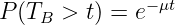 | (5.5.1) |
mit der mittleren Enderate μ, mit der Belegungen zu Ende gingen, wenn nur eine Leitung vorhanden wäre.
Für die Wahrscheinlichkeitsdichte für Belegungszeiten kleiner TB mit
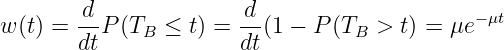 | (5.5.2) |
ergibt dessen Erwartungswert die mittlere Dauer einer Belegung (Zeidler, 2003, Seite 170, Integral 417)
Das Integral lässt sich mathematisch mit Partieller Integration
![∫ ∫
′ ′
g(x) ⋅ f (x )dt = [g(x) ⋅ f (x)] − g(x) ⋅ f(x)dt](kt65x.png)
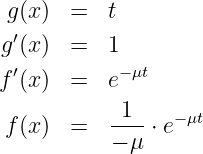
![∫ [ ]∞ ∫
∞ t ⋅ e−μtdt = t ⋅-1--⋅ e−μt + 1- ∞ e−μtdt
0 − μ μ 0
[ ]∞ 0 [ ]∞
= − 1- t ⋅ e− μt − -1-⋅ e−μt
μ 0 μ2 0
-1-[ −μt ]∞ 1--
= μ2 e (− μt − 1) 0 = μ2](kt67x.png)
Summiert man die Zeitabschnitte ti der tatsächlichen Belegungen auf, so erhält man die Verkekehrsmenge
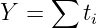 | (5.5.4) |
Daraus ergibt sich die (gemessene) mittlere Belegungsdauer
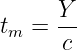 | (5.5.5) |
durch Division durch die Anzahl c der Belegungen. Durch eine Normierung auf die Beobachtungszeit T ergibt sich die bei der Hauptverkehrsstunde eingeführte Verkehrsmenge zu
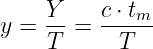 | (5.5.6) |
Bei einer Überschreitung der Leistung eines Systems, wenn also das Angebot
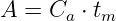 | (5.5.7) |
die Anzahl von Belegungsversuchen pro Zeitabschnitt Ca multipliziert mit der mittleren Belegungsdauer, die Belastung oder die maximale Leistung des Systems
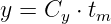 | (5.5.8) |
die Anzahl von erfolgten Belegungen pro Zeitabschnitt Cy multipliziert mit der mittleren Belegungsdauer, überschreitet muss der Restverkehr
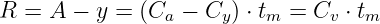 | (5.5.9) |
Der Verlust B bezogen auf das Angebot A ist damit
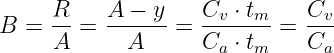 | (5.5.10) |
mit den Verlustbelegungen Cv, die aus Kapazitätsmangel abgewiesen werden.
Man spricht von einem Wartesystem, wenn die während der Blockierungsdauer eintreffenden Belegungen so lange in einem Wartespeicher gehalten werden, bis sie eine freigewordene Verbindung belegen.
→ Die Belastung des Systems entspricht dem Angebot!
→ Es ergibt sich eine Wartedauer während der Blockierung!
Die Wahrscheinlichkeit einer Wartezeit ergibt sich mit der Anzahl der verzögerten Belegungen Cw > 0 zu
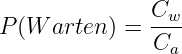 | (5.5.11) |
Dabei entsteht eine mittlere Wartedauer bezogen auf die Summe der Wartezeiten tw,ges aller Gespräche von
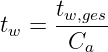 | (5.5.12) |
und bezogen auf die Summe der Wartezeiten der wartenden Gespräche von
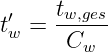 | (5.5.13) |
Durch Messen der Belegungen der Leitungen eines TK-Systems kann man die Statistik der Einfallsabstände TA angeben. Für diesen gedächtnislosen Bedienprozess erhält man (ebenfalls) eine Exponentialverteilung für Einfallsabstände größer als t
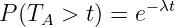 | (5.5.14) |
mit der mittleren Ankunftsrate λ = λq ⋅ m bei m Quellen mit der mittleren Ankunftsrate λq je Quelle.
Für die Wahrscheinlichkeitsdichte für Einfallszeiten kleiner t mit3
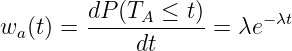 | (5.5.15) |
ergibt dessen Erwartungswert analog den mittlerer Einfallsabstand
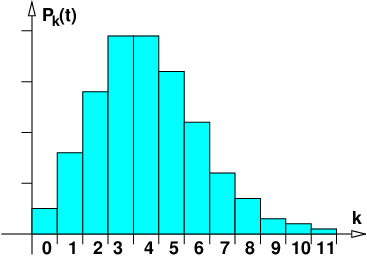
Die Wahrscheinlichkeit Pk(t) von k einfallenden Belegungenswünschen innerhalb einer Zeit T kann mit der Poisson-Verteilung
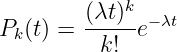 | (5.5.17) |
beschrieben werden.
Endlicher Automat mit Zuständen und Übergängen, die beschreiben, wie das System von einem Zustand aus in einen anderen wechseln darf und was beim Übergang passiert
Markov-Kette als Sonderfall mit Zustandsübergängen nur in benachbarte Zustände, mathematisch im stationärem Gleichgewicht
Stochastischer Automat mit Übergangswahrscheinlichkeiten (Zustandsübergangsraten) und Wahrscheinlichkeiten, dass sich das System jeweils in den einzelnen Zuständen befindet
Betrachtet man Abb. 5.5.2 als Darstellung der Belegung eines Telefonnetzes, wobei die numerierten Zustände die Anzahl der gleichzeitig im System befindlichen Belegungen darstellen, dann sind Übergänge
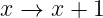 | (5.5.18) |
hinzukommende, neue Belegungen und umgekehrt entspricht ein Übergang
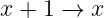 | (5.5.19) |
jeweils einer beendeten Belegung.
Die Pk(t) sind dann die Wahrscheinlichkeiten dafür, dass zu einem Zeitpunkt t gerade k Belegungen stattfinden.
→ Voraussetzung: Das System hätte für k gleichzeitige Belegungen auch immer genügend Kapazitäten.
→ Praxis: Verlust- oder Wartesysteme!
Dimensionierung der Netzkapazitäten mit bekannten Pk(t) mit der Erlangformel:
- Ziel z.B. im Mittel zum Zeitpunkt t Durchführung von 95% aller theoretischen Gespräche
- Im Zustand Pk kann ein dann noch neu hinzukommendes Gespräch mangels Kapazität nicht mehr bedient werden.
Zur Herleitung der Erlang-B-Formel werden folgende Annahmen gemacht:
- Das System befindet sich im stationären Gleichgewicht
→ Die Zahl der neuen Belegungen je Zustand ist in etwa gleich der Anzahl der in diesem Zustand beendeten Belegungen.
→ Sonst gäbe es nach kurzer Zeit entweder überhaupt keine Belegung mehr im System -oder aber zig Millionen.
- Betrachtung desselben Zeitpunktes
→ Hauptverkehrsstunde (Busy Hour) wodurch die Zeitabhängigkeit t weg fällt.
Das ergibt folgende mathematische Aussagen4:
- Stationärbedingung für den ersten Zustand
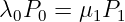
(5.5.20) → Die Wahrscheinlichkeit das sich das System aus dem Zustand 0 (keine Belegung) in den Zustand 1 begibt (genau 1 Belegung) ist genauso groß, wie die umgekehrte Änderung.
- Stationärbedingung für alle inneren Zustände
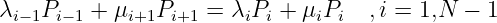
(5.5.21) - Stationärbedingung für den letzten Zustand
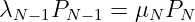
(5.5.22) - Und die Totale Wahrscheinlichkeit
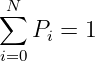
(5.5.23) → In einem der möglichen Zustände ist das System immer!
Mit vollständiger Induktion ergibt sich aus Gln. 5.5.20 die Induktionsannahme für k = 1
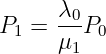 | (5.5.24) |
und entsprechend für k = 2
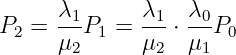 | (5.5.25) |
Nach Voraussetzung (für eine vollständige Induktion) gilt die Induktionsannahme für alle k ≤ x, also z.B. auch für
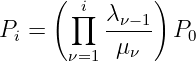 | (5.5.26) |
Für k = x + 1 erhalten wir dann aus der Stationärbedingung für alle inneren Zustände (Gln. 5.5.21)
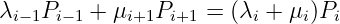 | (5.5.27) |
direkt durch einfache Umformung
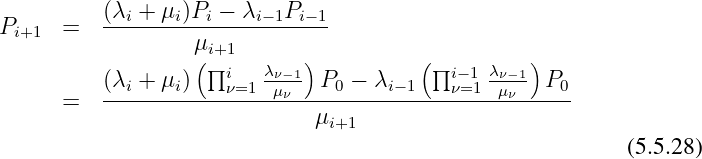
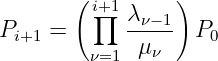 | (5.5.29) |
Gleichsetzen und Kürzen von
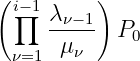 | (5.5.30) |
ergibt
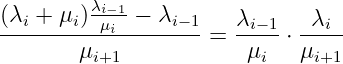 | (5.5.31) |
das sich nach Ausmultiplizieren der Klammer schnell als richtig erweist, wodurch die Induktionsannahme bewiesen wurde,.
Es folgt mit vollständiger Induktion aus Gln. 5.5.20 und Gln. 5.5.21
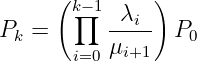 | (5.5.32) |
→ Das ist die erste Formel für die Zustandswahrscheinlichkeit eines allgemeinen Ankunftssystems.
→ Die Wahl von k Belegungen für dieses System bedeutet, dass die Blockkierungswahrscheinlichkeit dann gerade Pk wird.
Setzt man Gln. 5.5.32 in Gln. 5.5.23 ein, so erhält man
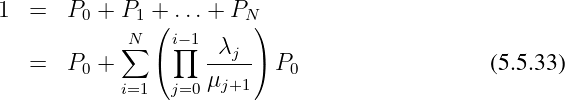
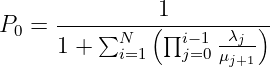 | (5.5.34) |
Setzt man nun Gln. 5.5.34 in 5.5.32 ein erhält man die Modellgleichung zur Beschreibung eines beleibigen Verlust- oder Wartesystems.
→ Für den Spezialfall eines Telefonsystems kommt man mit den folgenden Vereinfachungen direkt zur Erlangformel.
Um diese Gleichung zur Berechnung der Verlustwahrscheinlichkeit von Telefonsystemen zu verwenden setzt man:
- Die maximale Anzahl von Belegungen zu
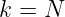
(5.5.35) → Bei mehr als k Belegungen geht dieses Mehr zu Verlust.
- Die Geburtsrate an neu hinzukommenden Belegungen ist
unabhängig davon, wieviele Belegungen bereits im System
geführt werden
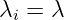
(5.5.36) → Das gilt für Systeme, bei denen die Quellenzahl wesentlich größer ist als die Zahl der Belegungen (Zufallsverkehr 1. Art).
- Die Sterberate an beendeten Belegungen ist proportional zu der
Anzahl der gerade aktiven Quellen.
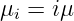
(5.5.37)
Setz man diese Annahmen in Gln. 5.5.32 ein mit k = N
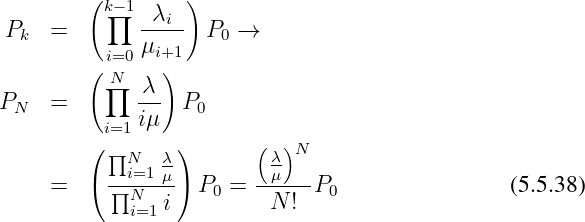
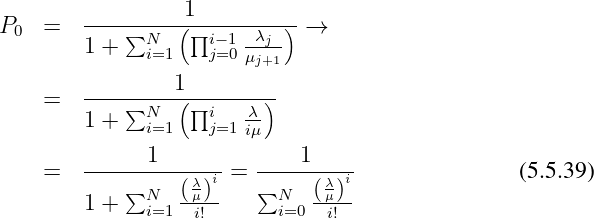
und setzt dieses wiederum ein, so erhält man
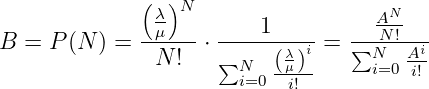 | (5.5.40) |
woraus sich mit dem Verkehrswert
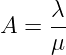 | (5.5.41) |
![∫ ∞ ∫ ∞ −μt
E {TB } = tm = t ⋅ w (t)dt = t ⋅ μe dt
[ −0μt ]∞ 0
= μ ⋅ e---(− μt − 1) = 1- (5.5.3)
μ2 μ
0](kt64x.png)