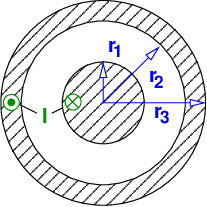
In einem langen geraden Leiter mit einem kreisförmigen Querschnitt fließt der Strom I.
In einem langen geraden Leiter mit kreisförmigen Querschnitt (Leiterradius = ro) fließt der Strom I.
Gesucht ist in allgemeiner Form die magnetische Feldstärke H in Abhängigkeit vom Abstand r von der Mittellinie innerhalb und außerhalb des Leiters. Der prinzipielle Verlauf der Funktion H = f(r) ist grafisch darzustellen.
Gesucht ist in allgemeiner Form die magnetische Feldstärke H in Abhängigkeit vom Abstand r von der Mittellinie in den Bereichen 0 ≤ r ≤ r1, r1 ≤ r ≤ r2, r2 ≤ r ≤ r3 und r ≥ r3.
Auf einem Keramikring sind N = 500 Windungen gleichmäßig am Umfang verteilt aufgebracht. Der mittlere Ringdurchmesser beträgt D = 50mm, der mittlere Windungsdurchmesser d = 6mm. In der Spule fließt der Strom I = 1,5A.
Auf einem Kunststoffring sind N = 1000 Windungen gleichmäßig am Umfang verteilt aufgebracht. Der mittlere Ringumfang beträgt l = 0,25m, die mittlere Windungsfläche A = 40mm2. In dem Ring soll der magnetische Fluss Φ = 0,4 ⋅ 10−6Wb erzeugt werden.
Welcher Strom I muss in der Spule fließen?
Eine Zylinderspule von l = 100mm Länge mit dem mittleren Windungsdurchmesser d = 6mm enthält N = 700 Windungen (μr = 1).
Welcher Strom muss in der Spule fließen, damit in der Spule der magnetische Fluss Φ = 5 ⋅ 10−8Wb erzeugt wird?
(Für die Berechnung kann näherungsweise die magnetische Spannung am Außenraum der Spule vernachlässigt werden.)
Zwei parallel verlaufende lange Leiter führen entsprechend Skizze die Ströme I1 = 12A und I2 = 16A (a = 8cm, b = 6cm, c = 7,5cm).
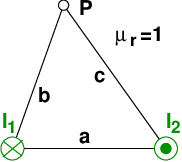
Drei parallel verlaufende lange Leiter führen entsprechend Skizze die Ströme I1 = I2 = 20A und I3 = 30A (a = 10cm).
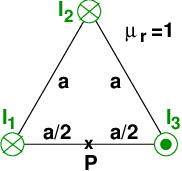
In zwei parallel verlaufenden langen geraden Leitern fließen die Ströme I1 = I2 = 50A (Skizze). Der Leiterradius beträgt r = 5mm, der Leiterabstand a = 25mm.
Wie groß ist die magnetische Feldstärke H auf der x-Achse an den Stellen
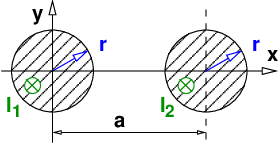
Skizzieren Sie anhand der berechneten Werte den Verlauf der einzelnen sowie der Summenfeldstärke im Bereich −r < x < a + r!
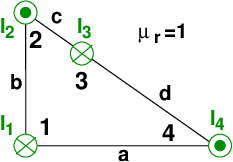
Drei parallel verlaufende lange gerade Leiter sind entsprechend Skizze angeordnet (a = 35mm, b = 45mm, c = 40mm, I1 = 30A, I2 = 35A, I3 = 40A).
Wie groß müssen die Ströme I2 und I4 sein, damit auf den Leiter 1 keine Kraft ausgeübt wird?
Ein dreieckförmiger Drahtrahmen befindet sich entsprechend Skizze in einem Magnetfeld der Flussdichte B = 1,0T (a = 5cm, b = 4cm, α = 70∘). In dem Leiter fließt der Strom I = 10A.
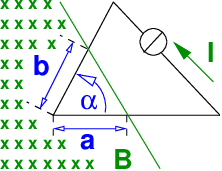
Es ist das auf die Leiterschleife ausgeübte Drehmoment M in Abhängigkeit vom Winkel α in allgemeiner Form anzugeben.
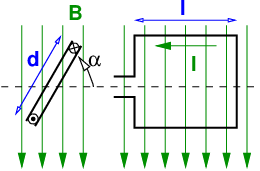
Ein Elektron (Ladung |e| = 1,6 ⋅ 10−19As, Masse m = 9,1 ⋅ 10−28g) trifft mit der Geschwindigkeit v = 10.000km∕s in ein homogenes Magnetfeld der Flussdichte B = 10−3T ein. Zwischen der Feldrichtung und der Bewegungsrichtung des Elektrons besteht ein rechter Winkel.
Wie groß ist der Radius der Kreisbahn, auf der sich das Elektron im Magnetfeld bewegt?
Auf einem Ringkern aus legiertem Blech mit dem mittleren Ringumfang l = 25cm (Magnetisierungskennlinie siehe Abb. 12.11.1 auf Seite §) ist eine Spule mit N = 500 Windungen aufgebracht.
Welcher Strom I muss in der Spule fließen, damit im Kern eine magnetische Flussdichte von B = 1,0T herrscht?
Bei dem angegebenen Kern aus Stahlguss (Magnetisierungskennlinie siehe Abb. 12.11.1 auf Seite §) soll im Luftspalt die Flussdichte B = 0,8T herrschen. Auf dem Kern ist eine Spule mit N = 800 Windungen aufgebracht (mittlere Eisenlängen: l1 = 30cm, l2 = 10cm).
(Für die Berechnung kann die magnetische Streuung vernachlässigt werden; Luftspaltfläche = Eisenquerschnitt)
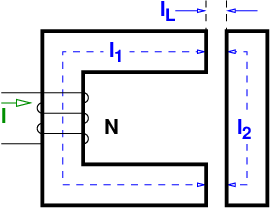
Ein Ringkern aus legiertem Blech (Magnetisierungskennlinie siehe Abb. 12.11.1 auf Seite §) mit einem mittleren Ringumfang von l = 40cm besitzt einen Eisenquerschnitt A = 3cm2. Auf dem Kern sind zwei Spulen mit den Windungszahlen N1 = 250 und N2 = 400 aufgebracht, die von den Strömen I1 = 1,0A und I2 = 0,5A durchflossen werden.
(Die Eisenlänge ist unverändert l = 40cm. Die magnetische Streuung ist zu vernachlässigen; Luftspaltfläche = Eisenquerschnitt.)
Mit welcher Kraft F ziehen sich die beiden Eisenteile bei dem Spulenstrom I = 3,0A an, wenn die Permeabilitätszahl des Eisens μr = 3000 beträgt?
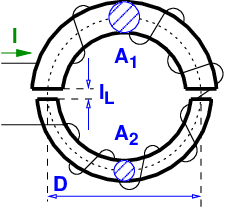
Welcher Strom I muss in der Spule fließen, wenn deren Windungszahl N = 700 beträgt? (Die magnetische Streuung ist zu vernachlässigen.)
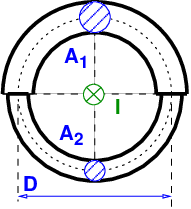
Welcher Strom I fließt im Leiter? (Für die Berechnung kann die Luftspaltlänge als vernachlässigbar klein angenommen werden.)
Mit welcher Kraft F ziehen sich beide Eisenteile an, wenn die Luftspaltlänge als vernachlässigbar klein und die Permeabilitätszahl des Eisens als μr = 3500 angenommen wird?
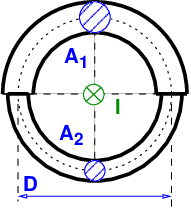
Ein Ringkern aus Eisen enthält eine Spule mit N = 50 Windungen. Der in der Spule fließende Strom I = 1A erzeugt im Kern die magnetische Flussdichte B = 0,8T .
Auf welchen Wert I′ muss der Spulenstrom erhöht werden, wenn in den Kern ein Luftspalt von lL = 0,4mm Länge eingefügt wird und die Flussdichte unverändert B = 0,8T betragen soll?
(Die magnetische Streuung ist zu vernachlässigen; Luftspaltfläche = Eisenquerschnitt. Es kann angenommen werden, dass die Eisenlänge unverändert bleibt.)
Ein Eisenkern aus legiertem Blech mit dem Kernquerschnitt A = 20cm2 (Magnetisierungskennlinie siehe Abb. 12.11.1 auf Seite §) enthält eine Spule, die vom Strom I = 1A durchflossen wird. Der dabei im Kern vorhandene magnetische Fluss beträgt Φ = 1,3 ⋅ 10−3Wb.
Auf welchen Wert I′ muss der Spulenstrom erhöht werden, damit der magnetische Fluss doppelt so groß wird?
Ein stromdurchflossener Leiter ist entsprechend Skizze von einem aus zwei Teilen bestehenden Eisenkern umgeben. In dem Leiter fließt der Strom I = 800A.
Mit welcher Kraft F ziehen sich die beiden Eisenteile an, wenn für die Berechnung der magnetische Widerstand des Eisens vernachlässigt wird? (Luftspaltfläche = Eisenquerschnitt)
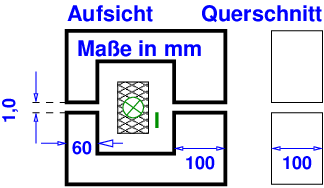
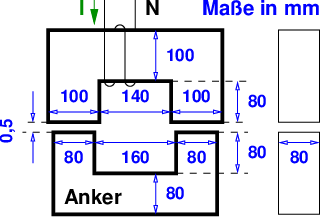
Bei dem skizzierten Elektromagneten soll der Anker mit der Kraft F = 800N angezogen werden. Die Windungszahl der Spule beträgt N = 100.
Welcher Strom I muss in der Spule fließen, wenn für die Berechnung der magnetische Widerstand des Eisens vernachlässigt wird? (Luftspaltfläche = Eisenquerschnitt)
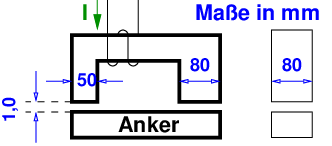
Zusatzfrage: Was müsste in der Aufgabenstellung geändert werden, damit der magnetische Widerstand des Eisens mit berücksichtigt werden kann?
Bei dem angegebenen Eisenkern ist auf dem Mittelschenkel eine Spule mit N = 120 Windungen aufgebracht, die vom Strom I = 0,2A durchflossen wird. Die Permeabilitätszahl kann als μr = 3500 angenommen werden.
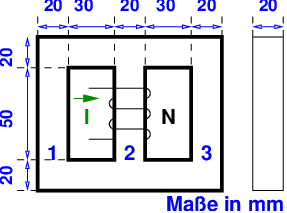
Bei einem Ringkern aus Eisen (mittlerer Ringumfang l = 30cm, Eisenquerschnitt A = 2cm2) kann die Magnetisierungskennlinie bis zu einer Flussdichte von B = 0,8T als Gerade angesehen werden. Die Permeabilitätszahl beträgt hier μr = 5000. Auf dem Kern ist eine Spule mit N = 1000 Windungen aufgebracht.
Auf einem Keramikring mit kreisförmigem Querschnitt sind N = 800 Windungen gleichmäßig am Umfang verteilt aufgebracht. Der mittlere Ringdurchmesser beträgt D = 80mm, der mittlere Windungsdurchmesser d = 12mm.
Wie groß ist die Induktivität L der Spule?
Welche Luftspaltlänge lL ist auf beiden Seiten des Kerns vorzusehen, damit die Induktivität der Spule L = 0,1H beträgt?
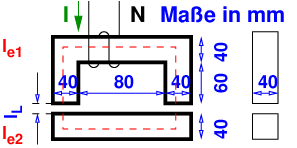
(Für die Berechnung ist die magnetische Streuung zu vernachlässigen: Luftspaltfläche = Eisenquerschnitt.)
