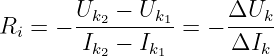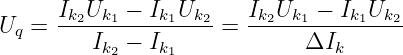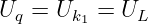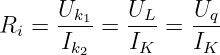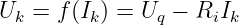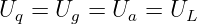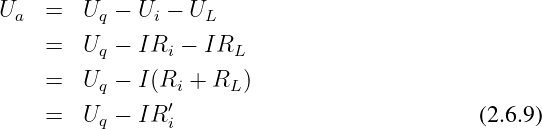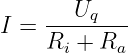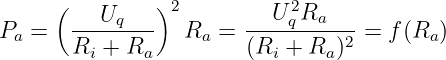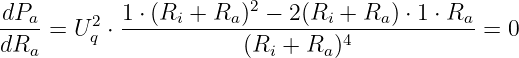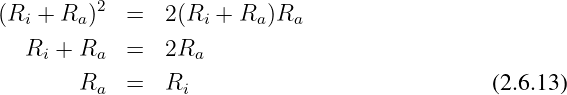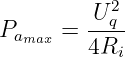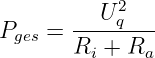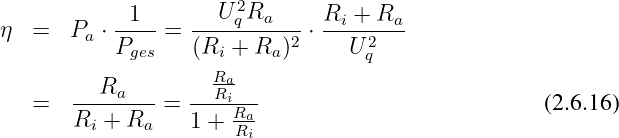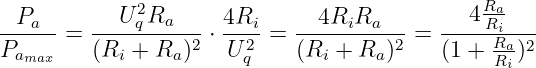2.6 Spannungsquelle

Praxis:

Spannungsquellen enthalten – genauso wie Verbraucher – elektrische Bauelemente, z.B. Kupferdraht, Dioden, Kondensatoren oder Spulen in Transformatoren, die einen endlichen spezifischen Widerstand haben und das Verhalten der realen Spannungsquelle bestimmen.

---

Abbildung 2.6.1: Ersatzschaltbild einer realen Spannungsquelle

---

Quelle:

Gegeben sei eine reale Spannungsquelle entsprechend Abb. 2.6.1 mit der Quellenspannung U_q und dem Innenwiderstand R_i. Diese Werte sind von außen nicht direkt zugänglich. Es stehen nur Klemmenspannung U_k und Strom I_k zur Verfügung.

2.6.1 Ersatzschaltbild

Frage:

Wie können Quellenspannung und Innenwiderstand des Ersatzschaltbildes (ESB) bestimmt werden?

→ Für 2 Unbekannten benötigen wir 2 Gleichungen!

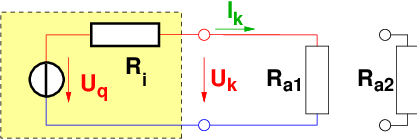
Messung:

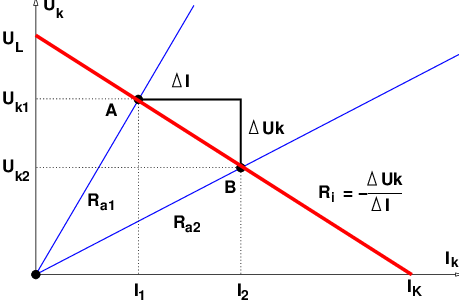
Um die Größen zu bestimmen, werden 2 verschiedene Widerstände R_a1 und R_a2 an die Spannungsquelle angeschlossen.

→ Dabei werden die Klemmenspannungen und die Ströme zu (U_k1,I_k1) und (U_k2,I_k2) gemessen.

Innenwiderstand:

Für jeden Außenwiderstand gilt in der Masche in Abb. 2.6.1

Da U_q = const ist (ideale Quelle) erhalten wir durch Gleichsetzen den Innenwiderstand zu

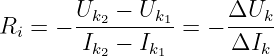(2.6.3)

→ Im Allgemeinen geht also eine Erhöhung des Stromes mit einer Verringerung der Klemmenspannung einher.

Quellenspannung:

Für die Quellenspannung ergibt sich mit „etwas“ Mathematik¹⁷ aus den Gln. 2.6.1 und 2.6.2

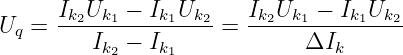(2.6.4)

Leerlauf:

Für den speziellen Außenwiderstand R_a1 = ∞ erhält man aus der gemessenen Leerlaufspannung U_L = U_k1 mit I_L = I_k1 = 0 die Quellenspannung direkt zu

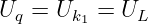(2.6.5)

Kurzschluss:

Für den speziellen Außenwiderstand R_a2 = 0 erhält man aus dem gemessenen Kurzschlussstrom I_K = I_k2 mit U_K = U_k2 = 0 den Innenwiderstand direkt zu

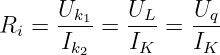(2.6.6)

→ Auch für reale Quellen gilt das Ohmsche Gesetz!

2.6.2 Kennlinie

Kennlinie:

Die Klemmenspannung der realen Spannungsquellen wird mit der Maschenregel zu

(2.6.7)

---

Abbildung 2.6.2: Betriebskennlinie einer realen Spannungsquelle

---

→ Die rote Gerade in Abb 2.6.2 ist die Arbeitsgerade der realen Quelle¹⁸

Punkte:

• Der Innenwiderstand R_i entspricht der Steigung der Kennlinie.
• Die Punkte (A) und (B) sind die Arbeitspunkte im Messversuch mit beliebigen Widerständen R_a1 und R_a2.
• Die durch den Nullpunkt und die Punkte (A) und (B) gehenden Geraden sind die Widerstandsgeraden. Sie werden durch das Ohmsche Gesetz für die Widerstände definiert.

Ideal:

Das Ziel für eine „möglichst“ ideale Quelle ist eine weitgehend unabhängige Stromentnahme.

→ Möglichst waagerechte Kennlinie mit kleinem Innenwiderstand.

Praxis:

Für einen Schutz der Quellen vor zu hohen Kurzschlussströmen durch zu kleine Verbraucher werden Sicherungen (als Schmelzsicherung oder Sicherungsautomat) in den Stromkreis eingebaut.

→ Eine reale Konstantspannungsquelle wird bei Überschreiten einer maximal zulässigen Stromstärke zu einer realen Konstantstromquelle.

2.6.3 Reale Spannungsquelle im realen Stromkreis

Leitung:

Bei einem realen Stromkreis ohne Vernachlässigungen muss neben dem Innenwiderstand R_i der Spannungsquelle noch der Leitungswiderstand R_L berücksichtigt werden wie dies in Abb. 2.6.3 dargestellt ist .

---

Abbildung 2.6.3: Vollständiges Ersatzschaltbild eines Stromkreises

---

Leerlauf:

Falls kein Strom fließt, ist die Quellenspannung U_q der idealen Quelle messbar

(2.6.8)

Belastung:

Ein Stromfluss erzeugt nach dem Ohmschen Gesetz an den Widerständen die Spannungsabfälle U_i = IR_i und U_L = IR_L. Mit Hilfe der Maschengleichung erhalten wir dann

Praxis:

Eine reale Leitung erhöht aus Sicht des Verbrauchers den Innenwiderstand der realen Quelle.

→ Der Leitungswiderstand realer Leitungen wird in Zukunft dem Innenwiderstand der realen Quelle zugerechnet!

2.6.4 Anpassung

Leistung:

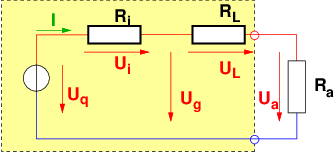
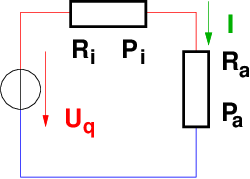
Die Leistung im Außenwiderstand in Abb. 2.6.4 ist nach Gln. 2.5.6 das Produkt aus Spannung am und Strom durch den Widerstand.

→ Die Leistung ist Null wenn entweder die Spannung am Widerstand (für R_a = 0, Kurzschluss) oder der Strom durch den Widerstand (für R_a = ∞, Leerlauf) Null sind.

---

Abbildung 2.6.4: Leistungsanpassung

---

Frage:

Wie verläuft die Funktion P_a = f(R_a), bzw. wo liegt das Maximum, das Leistungsmaximum, dieser Funktion?

→ Der Verbrauchswiderstand nutzt dann den maximal möglichen Anteil der von der Spannungsquelle abgegebenen Energie.

Funktion:

Für die Berechnung der Leistung P_a = I²R _a im Verbraucher benötigen wir den Strom durch die Reihenschaltung

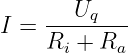(2.6.10)

Daraus ergibt sich die gesuchte Funktion zu

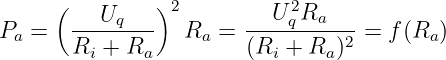(2.6.11)

Maximum:

Wie wir in der Mathematik gelernt haben, erhalten wir durch Nullsetzen der ersten Ableitung¹⁹ einer Funktion die Maxima

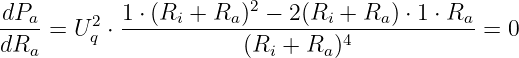(2.6.12)

Aus dem Zähler ergibt sich die Anpassbedingung zu

Kenngrößen:

Wir können nun folgende Kenngrößen berechnen

• Das Leistungsmaximum ergibt sich mit Gln. 2.6.11 bei Leistungsanpassung R_i = R_a zu

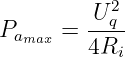  (2.6.14)

• Der Wirkungsgrad ergibt sich mit der Gesamtleistung

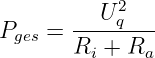  (2.6.15)

  zu

  
• Der Leistungsfaktor ist das Verhältnis der Ausgangsleistung zur maximalen Ausgangsleistung

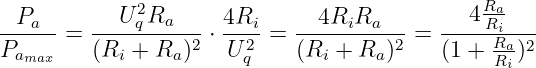  (2.6.17)

---

Abbildung 2.6.5: Wirkungsgrad η und Leistungsfaktor P_a∕P_amax in Abhängigkeit von x = R_a∕R_i

---

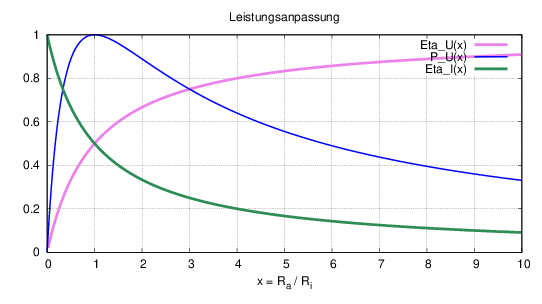
In Abb. 2.6.5 sind die Kenngrößen graphisch dargestellt, inklusive des Wirkungsgrades einer Stromquelle, der im folgenden Kapitel besprochen wird.

Nachricht:

In der Nachrichtentechnik sollen geringe Signalleistungen fehlerfrei und sicher durch einen Nachrichtenkanal übertragen werden

→ Leistungsanpassung P_a = P_amax zwischen den Stufen bei R_a = R_i.

Energie:

In der Energietechnik sollen erzeugte große Energien möglichst ohne Verluste vom Generator zum Verbraucher transportiert werden

→ Möglichst großer Wirkungsgrad η bei R_a ≫ R_i