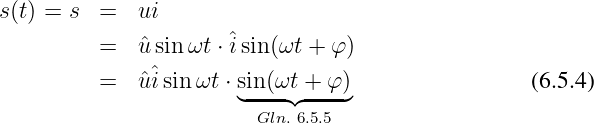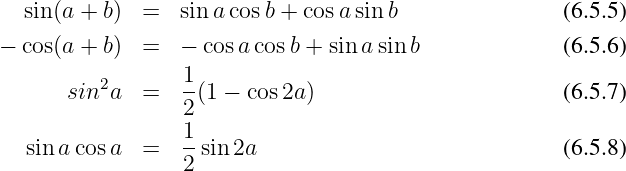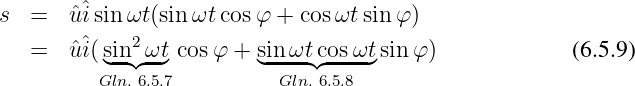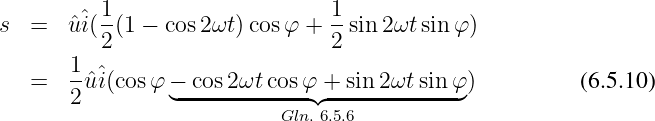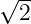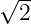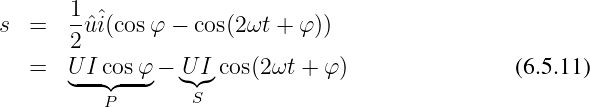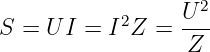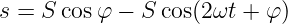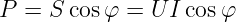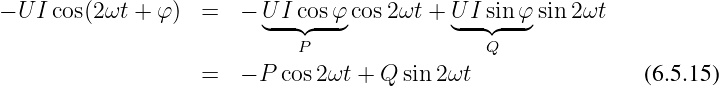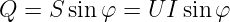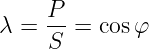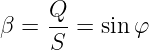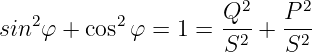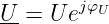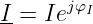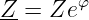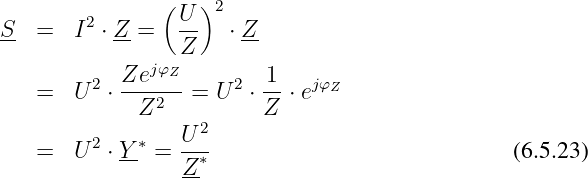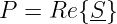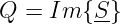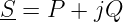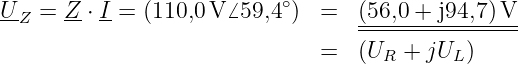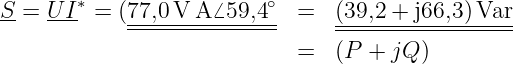Allgemeiner Wechselstromzweipol

6.5 Allgemeiner Wechselstromzweipol

Zweipol:

Als Wechselstromzweipol (siehe Abb. 6.5.1 bezeichnet man eine beliebige Kombination der Einzelelemente Widerstand (Wirkwiderstand R), Kondensator (Kapazität C) und Spule (Induktivität L), die nach außen durch zwei Anschlüsse elektrisch charakterisierbar ist.

Abbildung 6.5.1: Netzwerk als Wechselstrom-Zweipole

→ Die dargestellte Parallelschaltung stellt nur eines von vielen möglichen Netzwerken dar, deren Impedanz bestimmt werden kann aus

einer Messung von Spannung und Strom oder
einer Netzwerkberechnung mit den Bauelentewerten.

6.5.1 Spannung, Strom und Phasenwinkel

Messung:

Ebenso wie bei einem „einfachen“ Zweipol mit einem idealen Bauelement ergibt der Quotient aus der Spannung U und dem Strom I über das ohmsche Gesetz die Impedanz zu

U- jφZ Z-= I-= Ze

(6.5.1)

→ Ebenso kann der komplexe Leitwert oder die Admittanz berechnet werden. Oder einfacher als Kehrwert der Impedanz zu

Y = I-= --1---= 1-e−jφZ = Y ejφY -- U- ZejφZ Z

(6.5.2)

Kehrwerte:

Damit gilt auch für die komplexen Wechselgrößen

1- Z-= Y-

(6.5.3)

→ Das gilt aber i.a. nicht für den Real- und Imaginär getrennt!

Phasenwinkel:

Durch den induktiven Anteil (X_L > 0) und den kapazitiven Anteil (X_C < 0) wird der resultierende Phasenwinkel φ beschränkt. In Abb. 6.5.2 sind Zeigerdarstellungen für einige spezielle komplexe Widerstände bzw. Leitwerte dargestellt.

Abbildung 6.5.2: Komplexer Widerstand und Leitwert: Zusammenstellung der Impedanzen und Admittanzen für exemplarische Fälle

6.5.2 Leistung im Zeitbereich

Leistung:

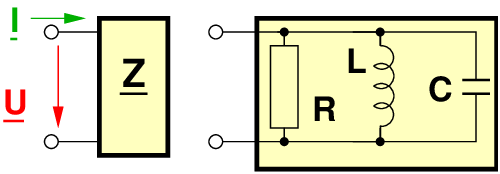
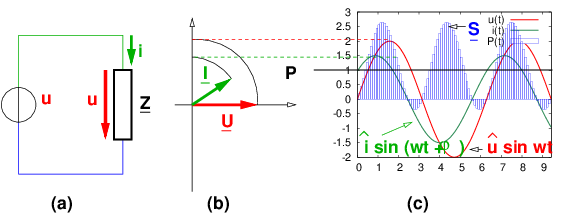
Aufgrund der Spannung u = û sin ωt fließt durch die Impedanz Z der Strom i = î sin(ωt + φ) (siehe Abb. 6.5.3) .

→ Wie groß sind die Schein-, Wirk- und Blindleistungen?

Abbildung 6.5.3: Scheinleistung beim allgemeinen Zweipol

Zeitwerte:

Für den Zeitwert der Leistung erhalten wir dann

s(t) = s = ui ˆ = ˆusinωt ⋅isin(ωt + φ ) = ˆuˆisin ωt ⋅ sin(ωt + φ) (6.5.4) ◟----◝◜---◞ Gln.6.5.5

Theorem:

Im folgenden benötigen wir diese vier mathematischen Additionstheoreme

sin(a + b) = sin acos b + cos asinb (6.5.5) − cos(a + b) = − cosa cosb + sin asin b (6.5.6) 2 1- sin a = 2(1 − cos2a ) (6.5.7) 1 sin acos a = --sin 2a (6.5.8) 2

Rechnung:

Wir setzen Additionstheorem 6.5.5 in Gln. 6.5.4 ein

s = ˆuˆisin ωt(sin ωt cosφ + cos ωtsinφ ) ˆ 2 = ˆui(s◟in◝ω◜t◞cos φ + s◟inωt◝c◜osωt◞sin φ) (6.5.9) Gln.6.5.7 Gln.6.5.8

und mit den beiden Additionstheoremen Gln. 6.5.7 und 6.5.8 ergibt sich weiter

s = ˆuˆi(1-(1 − cos 2ωt)cos φ + 1-sin 2ωt sin φ) 2 2 1- ˆ = 2 ˆui(cosφ −◟-cos2ωt-cosφ◝+◜--sin-2ωt-sin-φ◞) (6.5.10) Gln.6.5.6

Ergebnis:

Wir verwenden nun das Additionstheorem Gln. 6.5.6 und erhalten mit den Effektivwerten U = û∕ √ --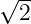
2 und I = î∕ 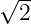das Ergebnis

s = 1-ˆuˆi(cosφ − cos(2ωt + φ )) 2 = U I cosφ − U I cos(2ωt + φ) (6.5.11) ◟--◝◜---◞ ◟◝S◜◞ P

Scheinleistung:

Das Produkt

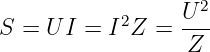2 2 U-- S = UI = I Z = Z

(6.5.12)

wird in Analogie zum Scheinwiderstand als Scheinleistung des Zweipols bezeichnet. Wir können Gln. 6.5.11 damit einfacher schreiben als

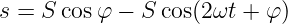s = S cos φ − S cos(2ωt + φ)

(6.5.13)

Es wird ein konstanter Wert der Leistung, S cos φ, von einer Leistungsschwingung, S cos(2ωt + φ), mit doppelter Frequenz 2ω überlagert.

Wirkleistung:

Der konstante Anteil der Scheinleistung ist die Wirkleistung

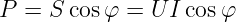P = S cosφ = UI cosφ

(6.5.14)

Blindleistung:

Für den zweiten Anteil der Scheinleistung in Gln. 6.5.11 konnten wir mit dem Additionstheorem Gln. 6.5.6 schreiben

− U I cos(2ωt + φ ) = − U◟I-c◝o◜sφ◞cos2 ωt + U◟I-s◝in◜-φ◞sin 2ωt P Q = − P cos 2ωt + Q sin 2ωt (6.5.15)

Für die Wirkleistung hatten wir bereits P = UI cos φ eingeführt. Entsprechend gilt nun für die Blindleistung

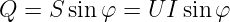Q = S sin φ = UI sin φ

(6.5.16)

Einheiten:

Nur zur besseren Unterscheidung der Leistungsarten werden diese Unterschiedlich bezeichnet: [P] = W (Watt), [S] = V A (Voltampere) und [Q] = Var (Voltampere reactive).

Leistungsfaktor:

Das Verhältnis von Wirkleistung zu Scheinleistung wird als Leistungsfaktor bezeichnet

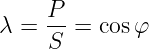P- λ = S = cosφ

(6.5.17)

→ Der Leistungsfaktor gibt an, welcher Anteil der Scheinleistung in Wirkleistung (z.B. Wärme, mechanische Arbeit) umgesetzt wird.

Blindfaktor:

Analog zum Leistungsfaktor definieren wir das Verhältnis von Blindleistung zu Scheinleistung als Blindfaktor

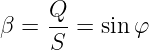Q β = -- = sin φ S

(6.5.18)

Bemerkung:

Aufgrund der trigonometrischen Beziehung

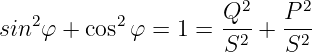2 2 sin2φ + cos2φ = 1 = Q--+ P-- S2 S2

(6.5.19)

erhalten wir aus Gln. 6.5.17 und Gln. 6.5.18

∘ --------- S = P2 + Q2 (6.5.20)

6.5.3 Komplexe Leistungsberechnung

Zeiger:

Aufgrund einer komplexen Spannung

U = U ejφU --

fließt der komplexe Strom

I-= IejφI

durch die Impedanz

Z-= Ze φ

und erzeugt dort die komplexe Leistung

U S- = ZI2 = --I2 I- UejφU 2 jφ −jφ = --jφI-I = U e U ⋅ Ie I (6.5.21) Ie

Mit dem konjugiert komplexen Strom I^∗ erhalten wir das Ergebnis

S-= UI-∗

(6.5.22)

Vorher:

Diese Darstellung entspricht der Leistungsdefinition für Gleichstrom mit

P = RI2

Warum ist die Scheinleistung dann nicht einfach

S- = U-⋅ I = UejφU ⋅ IejφI = U ⋅ Iej(φU+ φI)

Dieses ist aber ersichtlich falsch, da bei einem Widerstand Spannung und Strom in Phase sind, aber außer im Trivialfall φ_U + φ_I≠0 ist.

Alternativ:

Eine andere Darstellung entsprechend P = U²∕R erhält man mit

( U )2 S- = I2 ⋅ Z-= -- ⋅ Z- Z 2 ZejφZ- 2 1- jφZ = U ⋅ Z2 = U ⋅Z ⋅ e U 2 = U 2 ⋅ Y-∗ =-∗ (6.5.23) Z-

Komponenten:

Mit den Ergebnissen der Berechnung zur Zeitdarstellung ergibt sich die komplexe Leistung aus der Wirkleistung

P = Re {S-}

und der Blindleistung

Q = Im {S-}

S- = P + jQ

(6.5.24)

Beispiel 6.5.1 (RL-Reihe)

Eine unbekannte Spule L wird in Reihe mit dem Wirkwiderstand R = 80 Ω an die sinusförmige Wechselspannung 110 V und 50 Hz gelegt. Der Strommesser zeigt 0,7 A an. Berechnen Sie folgende Größen:

Scheinwiderstand und induktiver Widerstand
Induktivität der Spule und Phasenwinkel
Wirkspannung und Blindspannung
Scheinleistung, Wirkleistung und Blindleistung
Leistungsfaktor und
Zeichnen Sie das Zeigerdiagramm

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

$U 110V Z = -- = ------= 157,1-Ω- I 0,7A$
und
$√ --------- ∘ -------------------- XL = Z2 − R2 = (157,1Ω )2 − (80 Ω )2 = 135,2-Ω$
$XL-- -135-Ω- L = 2πf = 2π50 ∕s = 0,43-H-$
und
$∘ φ = 59,4-$
$∘ UZ = Z-⋅ I-= (110,0 V⁄ 59,4 ) = (56,0 +-j94,7)V- = (UR + jUL )$
$S-= U-I∗ = (77,0V-A-⁄ 59,4∘ = (39,2 +-j66,3)Var- --------------- ------------------ = (P + jQ )$

[next] [prev] [prev-tail] [front] [up]