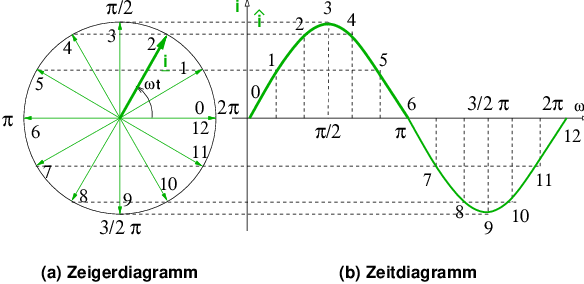
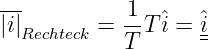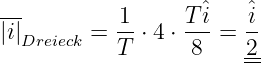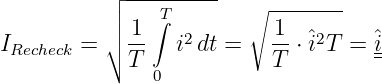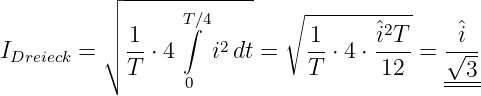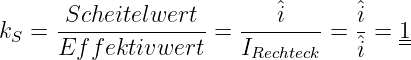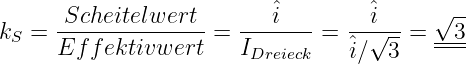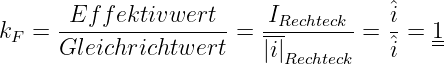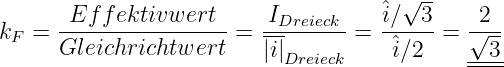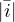Eigenschaften sinusförmiger WechselgröSSen

4.3 Eigenschaften sinusförmiger Wechselgrößen

Zeigerdiagramm:

Anstelle der Darstellung von Wechselgrößen im Zeitbereich kann ein Zeigerdiagramm verwendet werden.

→ Der Scheitelwert î der Wechselgröße in Abb. 4.3.1 entspricht der Länge des Zeigers i, der mit der Winkelgeschwindigkeit ω mathematisch positiv (also entgegen dem Uhrzeiger) dreht.

→ Bezugsachse: Willkürlich die Waagerechte.

Abbildung 4.3.1: Zusammenhang zwischen (a) Dreh-Zeigerdiagramm und (b) Zeitdiagramm

Kreisfrequenz:

Anstelle der Zeit t wird bei Sinusschwingungen im allgemeinen der proportionale Drehwinkel φ = ωt verwendet. Für die Kreisfrequenz ω einer Sinusschwingung gilt dann

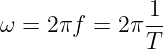1 ω = 2πf = 2π-- T

(4.3.1)

mit der Einheit [ω] = s⁻¹. Sie wird NICHT in Hertz angegeben!

Periodendauer:

Mit der Kreisfrequenz ω wird die Periodendauer einer Sinusschwingung dann analog

2 π T = --- ω

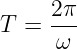(4.3.2)

Mittelwert:

Der arithmetische Mittelwert einer Wechselgröße muss definitionsgemäß Null sein. Für t₀ = 0 folgt mit Gln. 4.2.3 für den Mittelwert (mit ωT = 2π)

∫T ˆ ¯i = 1- ˆisin ωt dt = -−i-[cosωt]t=T T ωT t=0 0 -−ˆi- = ωT (cosωT − cos 0) = 0 (4.3.3)

Substitution:

Werden Sinusgrößen nicht als Funktion der Zeit t sondern als Funktion des Drehwinkels φ dargestellt

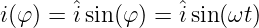i(φ) = ˆisin(φ) = ˆisin(ωt)

(4.3.4)

muss bei der Integration dann anstelle nach der Zeit dt nach dem Winkel dφ = d(ωt) integriert werden. Mit

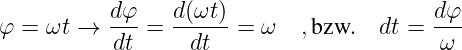dφ- d(ωt)- dφ- φ = ωt → dt = dt = ω ,bzw. dt = ω

(4.3.5)

und den entsprechenden Anfangs- und Endwerten

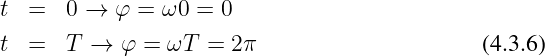
t = 0 → φ = ω0 = 0 t = T → φ = ωT = 2π (4.3.6)

Ergebnis:

Mit dieser Substitution kann alternativ

2∫π ˆ ¯i = -1- ˆisin(ωt) d(ωt) = −-i[cosωt]ωt=2π= 0 2π 0 2π ωt=0

(4.3.7)

berechnet werden, was aber zum selben Ergebnis führt⁴.

Phasenwinkel:

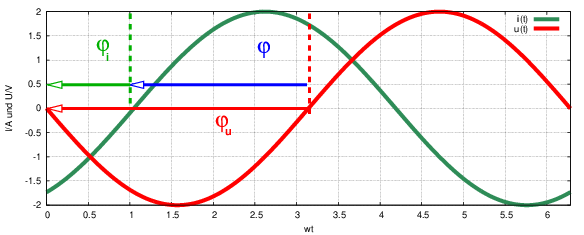
Ein sinusförmiger Strom entsprechend Abb. 4.3.2 kann beschrieben werden mit

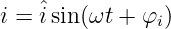i = ˆisin(ωt + φi)

(4.3.8)

und eine Spannung entsprechend mit

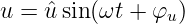u = ˆusin(ωt + φu )

(4.3.9)

Abbildung 4.3.2: Sinusförmiger Strom- und Spannungsverlauf mit Phasenverschiebung

Bezug:

In Gln. 4.3.8 ist φ_i der Nullphasenwinkel des Stromes i(t = 0) bezogen auf die y-Achse. Positive Winkel verschieben die Kurve nach links (in die Vergangenheit) und negative nach rechts.

→ φ_i = −60^∘ ist in Abb. 4.3.2 negativ, da der Nullpunkt des Stromes entgegen der eingezeichneten Zähl-Pfeilrichtung von der Bezugsachse verschoben ist. Tatsächlich wurde für Abb. 4.3.2 auch die Funktion i = 2A ⋅ sin(t − π∕3) verwendet.

→ φ_u = −180^∘ ist in Abb. 4.3.2 negativ, da der Nullpunkt der Spannung entgegen der Pfeilrichtung von der Bezugsachse verschoben ist. Auch hier wurde für Abb. 4.3.2 die Funktion u = 2V ⋅ sin(t − π) mit negativen Phasenwinkel verwendet.

Verschiebung:

Das Vorzeichen der Phasenverschiebung φ der Spannung gegen den Strom (Bezug Strom)

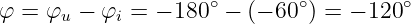φ = φu − φi = − 180 ∘ − (− 60∘) = − 120∘

(4.3.10)

ist ebenfalls negativ, da man den Nullpunkt des Stromes nach rechts (entgegen dem Zählpfeil, also negativ) verschieben müsste, um zum Nulldurchgang der Spannung zu kommen.

→ Der Strom eilt der Spannung voraus, d.h. der Nulldurchgang des Stromes in Abb. 4.3.2 ist (zeitlich) vor dem der Spannung.

Betrag:

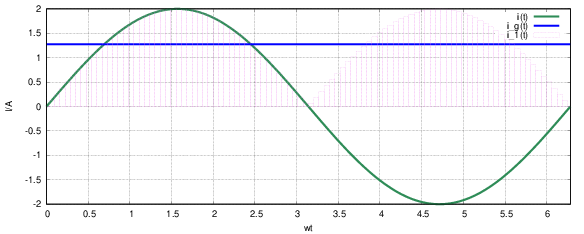
Da der arithmetische Mittelwert (Gleichwert) einer Wechselgröße definitionsgemäß Null ist, bildet man den arithmetischen Mittelwert aus dem Betrag der Wechselgröße⁵ entsprechend Abb. 4.3.3

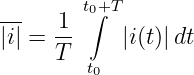--- t0+∫T |i| = -1 |i(t)|dt T t0

(4.3.11)

Abbildung 4.3.3: Gleichrichtwert eines sinusförmigen Stromes

Berechnung:

Mit Gln. 4.3.11 berechnet sich der Gleichrichtwert einer Sinusschwingung i = î sin ωt als Funktion von (ωt) zu

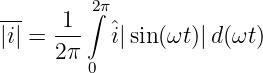∫2π |i| = -1- ˆi|sin(ωt)|d(ωt) 2π 0

(4.3.12)

Symmetrie:

Da nach der Gleichrichtung eine pulsierende Gleichspannung mit Periode π entsteht, vereinfacht sich die Berechnung mit |i(ωt)| = i(ωt) zu

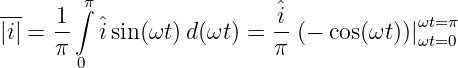∫π --- 1- ˆ ˆi- ωt=π |i| = π isin(ωt)d(ωt ) = π (− cos(ωt))|ωt=0 0

(4.3.13)

Einsetzen der Grenzen ergibt

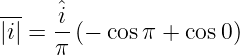ˆ |i|-= i-(− cosπ + cos0) π

(4.3.14)

Der Gleichrichtwert eines Sinusstromes ist dann

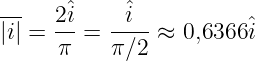--- 2ˆi ˆi |i| =-- = ----≈ 0,6366 ˆi π π∕2

(4.3.15)

Gleichrichtwert:

Bei Wechselgrößen kann die Betragsbildung mit einer Vollweg-Gleichrichterbrücke (Zweiwegegleichrichtung) erreicht werden.

→ Die negative Halbwelle einer Sinusgröße wird ins Positive geklappt.

→ Der arithmetische Mittelwert der gleichgerichteten Wechselgröße wird als Gleichrichtwert bezeichnet.

→ Die gelieferte elektrische Ladung einer Gleichrichterschaltung ist bei elektrolytischen Vorgängen oder beim Aufladen von Akkumulatoren von besonderer Bedeutung.

Vergleich:

Einem ohmschen Widerstand R, der an der Gleichspannung U angeschlossen ist, wird während der Zeit T die Energie

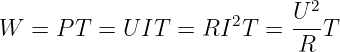2 W = PT = U IT = RI2T = U--T R

(4.3.16)

zugeführt. Welche Energie wird dem Widerstand in der gleichen Zeit an der Wechselspannung u zugeführt? Entspricht |i| = U?

Energie:

Bei der Umrechnung von Wechselgrößen in Gleichgrößen soll die mit der Leistung P oder der Energie W = PT verbundenen Kenngröße zu einer äquivalenten Leistungsberechnung führen. Für den ohmschen Widerstand bedeutet dieses

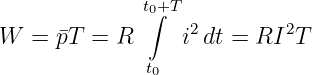t0∫+T W = ¯pT = R i2dt = RI2T t0

(4.3.17)

Abbildung 4.3.4: Effektivwert eines sinusförmigen Stromes

Effektivwert:

Der Effektivwert I = i_eff eines Wechselstromes kann demnach aus Gln. 4.3.17 so definiert werden, dass er einem Widerstand R in der Zeit T die gleiche Energie W zuführt wie ein Gleichstrom I mit

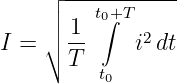┌ ----------- ││ 1 t0+∫T I = │∘ -- i2dt T t0

(4.3.18)

Bemerkung:

Die Augenblicksleistung
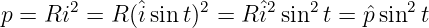
$p = Ri2 = R (ˆisint)2 = Rˆi2 sin2 t = pˆsin2 t$ (4.3.19)

wechselt periodisch zwischen Null und einem Maximalwert p.

Die Energie W einer Periode entspricht der schraffierten Fläche unter der Leistungskurve in Abb. 4.3.4 . Sie ist gleich der Rechteckfläche aus der mittlerer Leistung

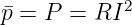
¯p = P = RI2

(4.3.20)

und der Periodendauer T , wie direkt aus Gln. 4.3.17 ersichtlich ist.

Berechnung:

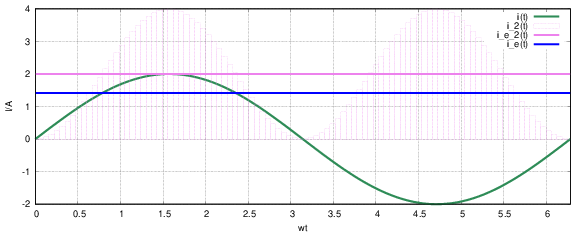
Mit Gln. 4.3.18 berechnet sich der Effektivwert einer Sinusschwingung

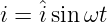
i = ˆisinωt

als Funktion von (ωt) zu

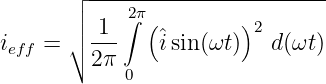┌ ----------------------- ││ 2∫π i = │∘ 1-- (ˆisin(ωt))2 d(ωt) eff 2π 0

(4.3.21)

Mittelwert:

Für die quadratische Funktion (siehe Abb. 4.3.4)

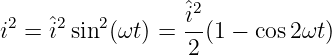ˆi2 i2 = ˆi2sin2(ωt) = --(1 − cos2ωt ) 2

(4.3.22)

wird der quadratische Mittelwert zu

ˆi2 ∫2π I2 = ------ (1 − cos2ωt )d(ωt) 2 ⋅ 2π 0 2 ⌊∫2π ∫2π ⌋ = --ˆi---⌈ d(ωt) − cos 2ωt d(ωt)⌉ 2 ⋅ 2π 0 0 --ˆi2-- 2π = 2 ⋅ 2π [(ωt)]0 (4.3.23)

Ergebnis:

Da der Mittelwert der Wechselgröße cos 2ωt definitionsgemäß Null ist, bleibt nur das erste Integral über mit dem Ergebnis der Integration

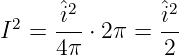2 2 I2 = ˆi--⋅ 2 π = ˆi 4π 2

(4.3.24)

Mit der Wurzel ergibt sich direkt der Effektivwert einer Sinusgröße zu

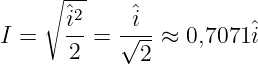∘ -2- I = ˆi- = √ˆi-≈ 0,7071ˆi 2 2

(4.3.25)

Scheitelfaktor:

Das Verhältnis des Scheitelwertes zum Effektivwert einer Wechselgröße mit beliebiger Kurvenform

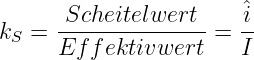ˆ kS = Scheitelwert---= i- Ef fektivwert I

(4.3.26)

wird als Scheitelfaktor bezeichnet.

Werte:

Speziell für einen Sinusstrom ergibt sich damit

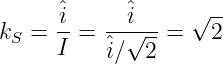ˆi- --ˆi-- √ -- kS = I = ˆi∕√2--= 2

(4.3.27)

Zahlenwerte für Scheitelfaktoren einfacher Kurvenformen sind


Kurvenform	k_S

Gleichgröße	1
Symmetrische Rechteckgröße	1
Sinusförmiger Größe	1,414
Symmetrisches Dreieckgröße	1,732

Formfaktor:

Das Verhältnis des Effektivwertes zum Gleichrichtwert einer Wechselgröße mit beliebiger Kurvenform

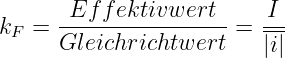-Ef-f-ektivwert-- I-- kF = Gleichrichtwert = |i|-

(4.3.28)

wird als Formfaktor bezeichnet. Speziell für einen Sinusstrom ergibt sich damit

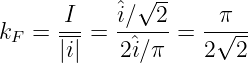√-- -I- ˆi∕--2- -π--- kF = |i| = 2ˆi∕π = 2√2--

(4.3.29)

Zahlenwerte für Formfaktoren einfacher Kurvenformen sind


Kurvenform	k_F

Gleichgröße	1
Symmetrische Rechteckgröße	1
Sinusförmiger Größe	1,111
Symmetrisches Dreieckgröße	1,155

Beispiel 4.3.1 (Kenngrößen)

Gegeben seien ein symmetrischer Dreieckstrom und ein symmetrischer Rechteckstrom mit der Periodendauer T = 2 s und dem Scheitelwert î = 2 A.

Wie groß sind die Gleichrichtwerte der beiden Ströme?
Wie groß sind die Effektivwerte der beiden Ströme?
Wie groß sind die Scheitelfaktoren der beiden Ströme?
Wie groß sind die Formfaktoren der beiden Ströme?

Hilfe:

Für alle, die in der Mathematik noch keine Integralrechnung hatten, hier die notwendigen Integrale und deren Stammfunktionen:

Fläche unter der Konstanten $i(t) = a$
in den Grenzen von t = u bis t = o:
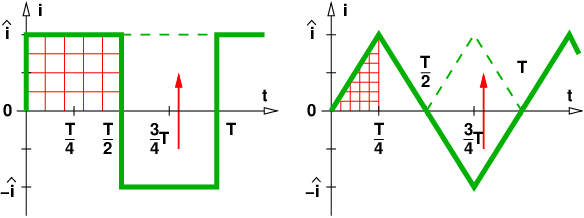
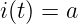
$∫o ∫o ∫o o i(t) dt = adt = a 1 dt = a [◟t]◝u◜◞ = a(o − u) u u u◟-◝◜-◞ Stammfunktion Integral$
Fläche unter der Geraden $i(t) = at$
in den Grenzen von t = u bis t = o:
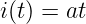
$∫o ∫o ∫o [ ]o ( ) i(t) dt = atdt = a tdt = a 1t2 = a- o2 − u2 -2 --u 2 u u u◟-◝◜-◞ Sta◟mmf◝u◜nk◞tion Integral$
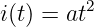
Fläche unter der Parabel $i(t) = at2$
in den Grenzen von t = u bis t = o:
$∫o ∫o ∫o [ ]o ( ) i(t)dt = at2 dt = a t2 dt= a 1-t3 = a- o3 − u3 u u u ◟3◝◜-u◞ 3 ◟--◝◜--◞ Stammfunktion Integral$
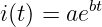
Fläche unter der e-Funktion $bt i(t) = ae$
in den Grenzen von t = u bis t = o:
$∫o ∫o ∫o [1 ]o a( ) i(t)dt = aebtdt = a ebtdt= a -ebt = --ebo − ebu u u u- -- ◟b◝◜--u◞ b ◟In◝te◜gra◞l Stammfunktion$

Lösung:

Die Lösung wird in der Vorlesung erarbeitet. Ergebnisse für den Vergleich der eigenen Lösung sind:

Gleichrichtwert Rechteckstrom $--- |i| = -1T ˆi = ˆi Rechteck T$
und Gleichrichtwert Dreieckstrom
$--- ˆ ˆ |i| = 1-⋅ 4 ⋅ Ti-=-i Dreieck T 8 2-$
Effektivwert Rechteckstrom $┌ --------- ││ T∫ ∘ -------- IRecheck = │∘ -1 i2dt = 1-⋅ˆi2T = ˆi T 0 T$
und Effektivwert Dreieckstrom
$┌│ ------------- ∘ ----------- ││ 1 T∫∕4 1 ˆi2T ˆi IDreieck = │∘ -- ⋅ 4 i2 dt = --⋅ 4 ⋅---= √--- T 0 T 12 --3-$
Scheitelfaktor Rechteckstrom $Scheitelwert ˆi ˆi kS = ---------------= --------= -= 1- Ef f ektivwert IRechteck ˆi$
und Scheitelfaktor Dreieckstrom
$Scheitelwert--- ---ˆi--- --ˆi- √ -- kS = Ef fektivwert = IDreieck = ˆi∕√3--= --3-$
Formfaktor Rechteckstrom $ˆ kF = -Ef-fektivwert---= -IRechteck- = i = 1- Gleichrichtwert |i|Rechteck ˆi$
und Formfaktor Dreieckstrom
$-- Ef fektivwert I ˆi∕√ 3 2 kF = -----------------= --Dreieck = ----- = √--- Gleichrichtwert |i|Dreieck ˆi∕2 --3-$

⁴Zur Kennzeichnung der Integrationsvariablen dφ = d(ωt) wird diese geklammert.

⁵Dabei ist zu beachten, dass der Betrag des Gleichrichtwertes |¯i| ≠|i| ist!

[next] [prev] [prev-tail] [front] [up]